Μάθημα : Α΄ΛΥΚΕΙΟΥ - ΑΛΓΕΒΡΑ

Δίνονται οι ανισώσεις: \(-x^{2}+5x-6<0, \text{ (1)}\) και \(x^{2}-16≤0, \text{ (2)}\)

α) Να βρεθούν οι λύσεις των ανισώσεων \((1), (2).\)
(Μονάδες 12)

β) Να παρασταθούν οι λύσεις των ανισώσεων \((1)\) και \((2)\) πάνω στον άξονα των πραγματικών αριθμών και να βρεθούν οι κοινές λύσεις των παραπάνω ανισώσεων.
(Μονάδες 13)

α) Το τριώνυμο \(-x^{2} + 5x - 6\) έχει \(α = - 1, β = 5, γ = - 6\) και διακρίνουσα: \(Δ = β^{2} - 4αγ= 5^{2} - 4 \cdot (-1) \cdot (-6)\)
\(= 25 - 24 =1 > 0\)

Οι ρίζες του τριωνύμου είναι οι:

$$x_{1,2} = \dfrac{−β± \sqrt{Δ}}{2α}$$ $$=\dfrac{−5±\sqrt{1}}{2 \cdot (-1)}=\dfrac{-5±1}{-2}$$ $$=\left\{\begin{array}{ll} x_{1}=\dfrac{-5+1}{-2} \\ x_{2}=\dfrac{-5-1}{-2}\end{array}\right.$$ $$= \left \{ \begin{array}{ll} x_{1}=2 \\ x_{2}=3 \end{array} \right.$$

Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.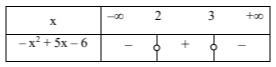

Επομένως ισχύει:

$$- x^{2} + 5x - 6 < 0$$ $$(x < 2 \text { ή } x > 3)$$ $$x \in (-∞, 2) \cup (3, +∞)$$

Ισχύει ότι:

$$\begin{align} & x^{2} - 16 ≤ 0 \\ & \Leftrightarrow x^{2} ≤ 16 \\ & \Leftrightarrow \sqrt{x^{2}} ≤ \sqrt{16} \\ & \Leftrightarrow |x| ≤ 4 \\ & \Leftrightarrow - 4 ≤ x ≤ 4 \\ & \Leftrightarrow x \in [- 4, 4] \end{align}$$

β) Παριστάνουμε τις λύσεις των παραπάνω ανισώσεων στον ίδιο άξονα αριθμών και όπως φαίνεται από το σχήμα που ακολουθεί:

οι κοινές λύσεις των δύο ανισώσεων είναι:

$$- 4 ≤ x < 2 \text{ ή } 3 < x ≤ 4$$ $$\Leftrightarrow x \in [- 4, 2) \cup (3, 4]$$

Δίνεται το τριώνυμο: \(-x^{2}+ \big( \sqrt{3} - 1 \big) x + \sqrt{3}\)

α) Να αποδείξετε ότι η διακρίνουσα του τριωνύμου είναι: \(Δ = \big( \sqrt{3} + 1 \big)^{2}\)
(Μονάδες 12)

β) Να παραγοντοποιήσετε το τριώνυμο.
(Μονάδες 13)

α) Το τριώνυμο \(- x^{2} +\big( \sqrt{3} - 1 \big) x + \sqrt{3}\) έχει \(α = - 1, β = \sqrt{3} - 1, γ = \sqrt{3}\) και διακρίνουσα:
\(Δ = β^{2} - 4αγ= \big( \sqrt{3} - 1 \big)^{2} - 4 \cdot (-1) \cdot \sqrt{3}\)
\(=\big( \sqrt{3} \big) ^{2} - 2 \sqrt{3} +1^{2} +4 \sqrt{3}\)
\(= \big( \sqrt{3} \big) ^{2} + 2 \sqrt{3} +1^{2}\)
\(= \big( \sqrt{3}+1 \big) ^{2}> 0\)

β) Οι ρίζες του τριωνύμου είναι οι:

$$x_{1,2} = \dfrac{−β± \sqrt{Δ}}{2α}$$ $$=\dfrac{− \big( \sqrt{3} - 1 \big) ± \sqrt{\big( \sqrt{3}+1 \big) ^{2}}}{2 \cdot (-1)}$$ $$=\dfrac{− \big( \sqrt{3} - 1 \big) ± \big( \sqrt{3}+1 \big)}{-2}$$ $$\left\{\begin{array}{ll} x_{1}=\dfrac{−\sqrt{3} +1+\sqrt{3}+1}{-2} \\ x_{2}=\dfrac{− \sqrt{3} + 1- \sqrt{3}-1}{-2}\end{array}\right.$$ $$= \left \{ \begin{array}{ll} x_{1}=\dfrac{2}{-2}=-1 \\ x_{2}=\dfrac{-2 \sqrt{3}}{-2}=\sqrt{3} \end{array} \right.$$

Επομένως:

$$ - x^{2} + \big( \sqrt{3}−1 \big) x + \sqrt{3}$$ $$=- \big( x - ( - 1)\big) \big( x−\sqrt{3} \big)$$ $$= - (x + 1) \big(x−\sqrt{3} \big)$$

α) Να λυθεί η εξίσωση: \(x^2 - x - 2 = 0\)
(Μονάδες 8)

β) Να λυθεί η ανίσωση: \(x^2 - x - 2 > 0\) και να παραστήσετε το σύνολο λύσεών της στον άξονα των πραγματικών αριθμών.
(Μονάδες 12)

γ) Να τοποθετήσετε το \(-\dfrac{4}{3}\) στον άξονα των πραγματικών αριθμών. Είναι το \(-\dfrac{4}{3}\)
λύση της ανίσωσης του ερωτήματος (β); Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 5)

α) Το τριώνυμο \(x^2 - x - 2\) έχει \(α = 1, β = - 1, γ = - 2\) και διακρίνουσα:

$$\begin{align} Δ & = β^2 - 4αγ \\ & = (-1)^2 - 4 \cdot 1 \cdot (- 2) \\ &= 1 + 8 \\ &= 9 > 0 \end{align}$$

Οι ρίζες του τριωνύμου είναι οι:

$$\begin{align} x_{1,2} & = \dfrac{−β±\sqrt{Δ}}{2α} \\ & =\dfrac{−(−1)±\sqrt{9}}{2 \cdot 1} \\ & =\dfrac{1±3}{2} \\ &=\begin{cases} \dfrac{1+3}{2}=2 \\ \dfrac{1-3}{2}=-1 \end{cases} \end{align}$$

β) Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.

Επομένως ισχύει:

$$x^2 - x - 2 > 0$$ $$(x < - 1 \text{ ή } x > 2)$$ $$x \in (-∞, - 1) \cup (2, +∞)$$

γ)

Το \(−\dfrac{4}{3}\) ανήκει στο διάστημα \((-∞, - 1)\), οπότε είναι λύση της ανίσωσης του ερωτήματος (β).

Δίνεται το τριώνυμο \(2x^2-3x+1\).
α) Να βρείτε τις ρίζες του.
(Μονάδες 10)

β) Να βρείτε τις τιμές του \(x\in\mathbb{R}\) για τις οποίες:

$$2x^2-3x+1 \lt 0 $$

(Μονάδες 5)

γ) Να εξετάσετε αν οι αριθμοί \(\dfrac{\sqrt{3}}{2}\) και \(\dfrac{1}{\sqrt{2}}\) είναι λύσεις της ανίσωσης:

$$2x^2-3x+1< 0$$

(Μονάδες 10)

α) Το τριώνυμο \(2x^2 - 3x + 1\) έχει \(α = 2, β = - 3, γ = 1\) και διακρίνουσα

\begin{align}Δ &= β^2 - 4αγ \\ &= (- 3)^2 - 4 \cdot 2 \cdot 1 \\ &= 9 - 8 \\ &= 1 > 0\end{align}

Οι ρίζες του τριωνύμου είναι οι:

\begin{align}x_{1,2} &= \dfrac{-β\pm\sqrt{Δ}}{2α}\\ &=\dfrac{-(-3)\pm\sqrt{1}}{2\cdot 2}\\ &=\dfrac{3\pm1}{4}\\ &=\begin{cases}\dfrac{3+1}{4}=1\\ \dfrac{3-1}{4}=\dfrac{1}{2}\end{cases}\end{align}

β) Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.

Επομένως ισχύει:

\begin{align}&2x^2 - 3x + 1 < 0 \\ \iff&\dfrac{1}{2} < x < 1 \\ \iff&x\in\left(\dfrac{1}{2},1\right)\end{align}

γ)

• Ο αριθμός \(\dfrac{\sqrt{3}}{2}\) ανήκει στο διάστημα \(\left(\dfrac{1}{2},1\right)\) διότι:

\begin{align}&\dfrac{1}{2}<\dfrac{\sqrt{3}}{2} < 1 \\ \iff&1 < \sqrt{3} < 2 \\ \iff&1^2 < \sqrt{3}^2 < 2^2 \\ \iff&1 < 3 < 4,\text{ ισχύει}\end{align}

• Ο αριθμός \(\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\) ανήκει στο διάστημα \(\left(\dfrac{1}{2},1\right)\) διότι:

\begin{align}&\dfrac{1}{2}<\dfrac{\sqrt{2}}{2} < 1 \\ \iff&1 < \sqrt{2} < 2 \\ \iff&1^2 < \sqrt{2}^2 < 2^2 \\ \iff&1 < 2 < 4,\text{ ισχύει}\end{align}

Τελικά οι αριθμοί \(\dfrac{\sqrt{3}}{2}\) και \(\dfrac{1}{\sqrt{2}}\) είναι λύσεις της ανίσωσης \(2x^2 - 3x + 1 < 0\).

α) Να λύσετε την εξίσωση:

$$\dfrac{|x+1|}{3}-\dfrac{|x+1|+4}{5}=\dfrac{2}{3}$$

(Μονάδες 9)

β) Nα λύσετε την ανίσωση:

$$- x^2 +2x +3\leq 0$$

(Μονάδες 9)

γ) Να εξετάσετε αν οι λύσεις της εξίσωσης του (α) ερωτήματος είναι και λύσεις της ανίσωσης του (β) ερωτήματος.
(Μονάδες7)

α) Είναι:

\begin{align}&\dfrac{|x+1|}{3}-\dfrac{|x+1|+4}{5}=\dfrac{2}{3} \\ \iff& 5|x + 1| - 3(|x + 1| + 4) = 5 \cdot 2 \\ \iff& 5|x + 1| - 3|x + 1| - 12 = 10 \\ \iff& 2|x + 1| = 22 \\ \iff& |x + 1| = 11 \\ \iff& (x + 1 = - 11 \text{ ή } x + 1 = 11) \\ \iff& (x = - 12 \text{ ή } x = 10)\end{align}

β) Το τριώνυμο \(- x^2 + 2x + 3\) έχει \(α = - 1, β = 2, γ = 3\) και διακρίνουσα:

\begin{align}Δ &= β^2 - 4αγ \\ &= 2^2 - 4 \cdot (-1) \cdot 3 \\ &= 4 + 12 \\ &= 16 > 0\end{align}

Οι ρίζες του τριωνύμου είναι οι:

\begin{align}x_{1,2} &= \dfrac{-β\pm\sqrt{Δ}}{2α}\\ &=\dfrac{-2\pm\sqrt{16}}{2\cdot(-1)}\\ &=\dfrac{-2\pm4}{-2}\\ &=\begin{cases}\dfrac{-2+4}{-2}=-1\\ \dfrac{-2-4}{-2}=3\end{cases}\end{align}

Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.

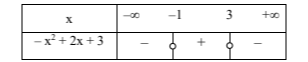
Επομένως ισχύει:

\begin{align}&- x^2 + 2x + 3 \leq 0 \\ \iff&(x \leq - 1 \text{ ή } x \geq 3) \\ \iff&x\in(-\infty, -1]\cup[3, +\infty)\end{align}

γ) Ο αριθμός \(- 12\) ανήκει στο διάστημα \((-\infty, -1]\) και ο αριθμός \(10\) ανήκει στο διάστημα \([3, +∞)\). Συνεπώς και οι δύο αριθμοί είναι λύσεις της δοθείσας ανίσωσης.

Θεωρούμε το τριώνυμο \(f(x)=x^2-x-3\).

α) Να βρείτε τις ρίζες του \(f(x)\).
(Μονάδες 12)

β) Να επιλύσετε την ανίσωση \(-2\cdot f(x) < 0\).
(Μονάδες 13)

α) Η διακρίνουσα του τριωνύμου είναι

\begin{align}Δ&=(-1)^2-4\cdot 1\cdot (-3)\\ &=1+12\\ &=13>0.\end{align}

Άρα το \(f(x)\) έχει δύο διαφορετικές πραγματικές ρίζες

$$x_1=\frac{-β-\sqrt{Δ}}{2α}=\frac{-(-1)-\sqrt{13}}{2\cdot 1}=\frac{1-\sqrt{13}}{2}$$

και

$$x_1=\frac{-β+\sqrt{Δ}}{2α}=\frac{-(-1)+\sqrt{13}}{2\cdot 1}=\frac{1+\sqrt{13}}{2}$$

β)

\begin{align}&-2\cdot f(x) < 0\\ \iff&-2\cdot \Big(-\frac{1}{2}\Big)\cdot f(x) > 0\cdot \Big(-\frac{1}{2}\Big)\\ \iff&f(x) > 0\end{align}

Κατασκευάζουμε τον πίνακα προσήμου του τριωνύμου, με βάση το (α) ερώτημα.
Καθώς είναι \(α=1 > 0\), παρατηρούμε ότι είναι \(f(x) > 0\) για

$$x\in\Big(-\infty,\dfrac{1-\sqrt{13}}{2}\Big)\cup\Big(\frac{1+\sqrt{13}}{2},+\infty\Big)$$

α) Να παραγοντοποιήσετε το τριώνυμο \(2x^2-x-1\).
(Μονάδες 12)

β) Να λύσετε την ανίσωση \(x(1-2x)\leq -1\).
(Μονάδες 13)

α) Επειδή \(α=2, β=-1\) και \(γ=-1\) η διακρίνουσα είναι

$$Δ= (-1)^2-4\cdot 2\cdot (-1)=9 > 0.$$

Το τριώνυμο έχει δύο άνισες ρίζες:

$$x_1=\frac{-(-1)+\sqrt{9}}{2\cdot 2}=\frac{4}{4}=1$$

και

$$x_2=\frac{-(-1)-\sqrt{9}}{2\cdot 2}=-\frac{2}{4}=-\frac{1}{2}.$$

Επομένως το τριώνυμο γίνεται

\begin{align}&\phantom{=}2x^2-x-1\\ &=2(x-1)\left(x+\frac{1}{2}\right)\\ &=(x-1)(2x+1)\end{align}

Άρα έχουμε

$$2x^2-x-1=(x-1)(2x+1).$$

β) Η ανίσωση γίνεται

\begin{align}&x(1-2x)\leq-1\\ \iff&-2x^2+x+1\leq 0\\ \iff&2x^2-x-1\geq 0.\end{align}

Έχουμε να λύσουμε ανίσωση δευτέρου βαθμού.
Παρατηρούμε πως το τριώνυμο της ανίσωσης είναι το τριώνυμο του πρώτου ερωτήματος. Άρα μηδενίζεται για \(x_1=1\) και \(x_2=-\frac{1}{2}\) και επειδή \(α=2 > 0\) προκύπτει:

Σύμφωνα με τον πίνακα προσήμων το τριώνυμο θα είναι ομόσημο του \(α\), δηλαδή θετικό για \(x\leq-\frac{1}{2}\) ή \(x\geq 1\).
Οι λύσεις της ανίσωσης είναι \(x\in(-\infty,-\frac{1}{2}]\cup [1,+\infty)\).

Δίνονται οι παραστάσεις

$$A=\frac{-x^2+4|x|-3}{|x|-1}$$

και

$$B=\frac{x^2-4|x|+4}{|x|-2}.$$

α) Για ποιες τιμές του \(x\in\mathbb{R}\) ορίζονται οι παραστάσεις \(Α\) και \(Β\);
(Μονάδες 8)
β) Να δείξετε ότι \(A=3-|x|\) και \(B=|x|-2\).
(Μονάδες 8)
γ) Να λύσετε την ανίσωση:

$$B-A < 2d(x,4)-5.$$

(Μονάδες 9)

ΛΥΣΗ
α) Η παράσταση \(Α\) ορίζεται όταν:

\begin{align}&|x|-1\neq 0\\ \iff&|x|\neq1\\ \iff&x\neq\pm1\end{align}

και η παράσταση \(Β\) όταν:

\begin{align}&|x|-2\neq0\\ \iff&|x|\neq2\\ \iff&x\neq\pm2\end{align}

β) Έχουμε:

$$-x^2+4|x|-3=-|x|^2+4|x|-3.$$

Θέτουμε \(ω=|x|\), οπότε

$$-|x|^2+4|x|-3=-ω^2+4ω-3,$$

που είναι τριώνυμο με ρίζες των οποίων το άθροισμα είναι

$$-\frac{β}{α}=-\frac{4}{-1}=4$$

και το γινόμενο είναι

$$-\frac{γ}{α}=\frac{-3}{-1}=3,$$

οπότε \(ω_1=3\) και \(ω_2=1\). Άρα

$$-ω^2+4ω-3=-(ω-1)(ω-3)$$

και

$$-|x|^2+4|x|-3=-(|x|-1)(|x|-3).$$

Συνεπώς:

\begin{align}A&=\frac{-x^2+4|x|-3}{|x|-1}\\ &=\frac{-(|x|-1)(|x|-3)}{(|x|-1)}\\ &=3-|x|.\end{align}

Για την παράσταση \(B\) έχουμε:

\begin{align}B&=\frac{x^2-4|x|+4}{|x|-2}\\ &=\frac{|x|^2-4|x|+4}{|x|-2}\\ &=\frac{(|x|-2)^2}{(|x|-2)}\\ &=|x|-2.\end{align}

γ) Η ανίσωση γίνεται:

\begin{align}&B-A < 2d(x,4)-5\\ \iff&|x|-2-3+|x| < 2|x-4|-5\\ \iff&2|x|-5 < 2|x-4|-5\\ \iff&|x| < |x-4|\\ \iff&|x|^2 < |x-4|^2\\ \iff&x^2 < (x-4)^2\\ \iff&x^2 < x^2-8x+16\\ \iff&x < 2\end{align}

Δεδομένου ότι για να έχει νόημα η ανίσωση πρέπει \(x\neq\pm1\) και \(x\neq\pm2\), τελικά η ανίσωση αληθεύει για

$$x\in(-\infty,-2)\cup(-2,-1)\cup(-1,1)\cup(1,2).$$

Δίνονται οι ανισώσεις \(|x-1|< 2\) και \(x^2-3x+2\geq0\).
α) Να βρείτε τις λύσεις τους.
(Μονάδες 8)

β) Να δείξετε ότι οι ανισώσεις συναληθεύουν για \(x\in(-1,1]\cup[2,3)\).
(Μονάδες 8)

γ) i. Αν οι αριθμοί \(ρ_1\) και \(ρ_2\), με \(ρ_1< ρ_2\), είναι κοινές λύσεις των ανισώσεων με \(ρ_1,ρ_2\in(-1,1]\), είναι και ο αριθμός \(\frac{ρ_1+3ρ_2}{4}\) κοινή τους λύση;
(Μονάδες 4)
ii. Αν οι αριθμοί \(ρ_1\) και \(ρ_2\), με \(ρ_1< ρ_2\), είναι κοινές λύσεις των ανισώσεων με \(ρ_1\in(1,1]\) και \(ρ_2\in[2,3)\), είναι και ο αριθμός \(\frac{ρ_1+3ρ_2}{4}\) κοινή τους λύση;
(Μονάδες 5)

α) Έχουμε:

\begin{align}&|x-2|< 2\\ \iff&-2< x-1< 2\\ \iff&-1< x< 3.\end{align}

Για να λύσουμε την ανίσωση \(x^2-3x+2\geq0\), θα βρούμε πρώτα τις ρίζες \(x_1\) και \(x_2\) του τριωνύμου. Έχουμε λοιπόν

$$x_1+x_2=\frac{-β}{α}=3$$

και

$$x_1\cdot x_2=\frac{γ}{α}=2,$$

οπότε \(x_1=1\) και \(x_2=2\).
Στη συνέχεια κατασκευάζουμε τον πίνακα προσήμου για το τριώνυμο \(x^2-3x+2\), με \(α=1>0\):

Οπότε η ανίσωση αληθεύει για \(x\in(-\infty,1]\cup[2,+\infty)\).

β) Με χρήση του άξονα των πραγματικών αριθμών,

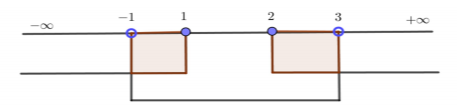
βλέπουμε ότι οι ανισώσεις συναληθεύουν για \(x\in(-1,1]\cup[2,3)\).

γ) Εφόσον οι αριθμοί \(ρ_1\) και \(ρ_2\), με \(ρ_1< ρ_2\), ανήκουν στο σύνολο των κοινών λύσεων των ανισώσεων, θα ισχύει \(ρ_1,ρ_2\in(-1,1]\cup[2,3)\).
i. Αν \(ρ_1,ρ_2\in(-1,1]\), τότε:

$$\begin{cases}-1< ρ_1\leq1\\-3<3ρ_2\leq3\end{cases}$$

και προσθέτοντας κατά μέλη προκύπτει:

$$-4<ρ_1+3ρ_2\leq4,$$

συνεπώς

$$-1<\frac{ρ_1+3ρ_2}{4}\leq1$$

και ο αριθμός \(\frac{ρ_1+3ρ_2}{4}\) είναι κοινή λύση των ανισώσεων.
ii. Αν \(ρ_1\in(-1,1]\) και \(ρ_2\in[2,3)\), τότε:

$$\begin{cases}-1<ρ_1\leq1\\6\leq3ρ_2<9\end{cases}$$

και προσθέτοντας κατά μέλη προκύπτει:

$$5<ρ_1+3ρ_2<10,$$

συνεπώς

$$\frac{5}{4}<\frac{ρ_1+3ρ_2}{4}<\frac{5}{2}$$

και ο αριθμός \(\frac{ρ_1+3ρ_2}{4}\) είναι κοινή λύση των ανισώσεων μόνο εάν

$$2\leq\frac{ρ_1+3ρ_2}{4}<\frac{5}{2}$$

α) Να λύσετε την εξίσωση \(x^4-16=0\quad (1)\).
(Μονάδες 8)

β) Να λύσετε την ανίσωση \(x^2+3x\leq 0\quad (2)\).
(Μονάδες 9)

γ) Να εξετάσετε εάν οι λύσεις της εξίσωσης \((1)\) είναι και λύσεις της ανίσωσης \((2)\).
(Μονάδες 8)

α) Έχουμε:

\begin{align}&x^4-16=0\\ \iff&x^4=16\\ \iff&x=\pm\sqrt[4]{16}\\ \iff&x=\pm2.\end{align}

Άρα οι λύσεις της εξίσωσης είναι \(x=2,\ x=-2\).

β) Για να λύσουμε την ανίσωση, θα βρούμε τις ρίζες του τριωνύμου \(x^2+3x\) και στη συνέχεια θα κάνουμε τον πίνακα προσήμου του \(x^2+3x\). Για να βρούμε τις ρίζες του τριωνύμου, παραγοντοποιώντας έχουμε:

\begin{align}&x^2+3x=0\\ \iff&x(x+3)=0\\ \iff&x=0\text{ ή }x=-3.\end{align}

Συνεπώς ο πίνακας προσήμου είναι ο παρακάτω:

Άρα η ανίσωση \((2)\) αληθεύει για \(x\in[-3,0]\).

γ) Από τις λύσεις της εξίσωσης \((1)\) μόνο η \(x=-2\) είναι και λύση της ανίσωσης \((2)\), διότι ανήκει στο διάστημα \([-3,0]\).

Δίνεται το τριώνυμο \(2x^2+3x-5\).

α) Να εξετάσετε αν το \(1\), είναι ρίζα του τριωνύμου
(Μονάδες 12)

β) Να παραγοντοποιήσετε το τριώνυμο.
(Μονάδες 13)

α) Παρατηρούμε ότι: \(2\cdot 1^2 + 3\cdot 1 -5=2+3-5=0\), οπότε το \(x_1=1\) είναι ρίζα του τριωνύμου.

β) Για να παραγοντοποιήσουμε το τριώνυμο, θα βρούμε και την δεύτερη ρίζα του χρησιμοποιώντας το γινόμενο των ριζών \(x_1 \cdot x_2=\dfrac{-5}{2}=-\dfrac{5}{2}\).
Οπότε:

$$x_1 \cdot x_2=-\dfrac{5}{2}$$ $$\Leftrightarrow 1 \cdot x_2=-\dfrac{5}{2}$$ $$x_2=-\dfrac{5}{2}$$

Άρα, το τριώνυμο \(2x^{2} + 3x - 5\) παραγοντοποιείται ως εξής:

\begin{align} 2x^{2} + 3x - 5 &= 2 (x - 1) \bigg( x - \Big( - \dfrac{5}{2} \Big) \bigg) \\ & = 2 (x - 1) \bigg( x + \dfrac{5}{2} \bigg) \\ & = (x-1) (2x+5) \end{align}

Δίνεται η εξίσωση \(x^2-2λx+λ^2-1=0\), με παράμετρο \(λ\in\mathbb{R}\).

α) Να αιτιολογήσετε γιατί η εξίσωση έχει, για οποιαδήποτε τιμή του \(λ\), πραγματικές και άνισες ρίζες.
(Mονάδες 6)

β) Να λύσετε την εξίσωση.
(Mονάδες 7)

Έστω \(ρ_1, ρ_2\) οι ρίζες της εξίσωσης με \(ρ_1 < ρ_2\).
γ) Να βρείτε για ποιες της παραμέτρου \(λ\), η απόσταση των αριθμών \(ρ_2\) και \(-ρ_1\) πάνω στον άξονα των πραγματικών αριθμών, είναι τουλάχιστον \(8\).
(Mονάδες 6)

δ) Θεωρούμε έναν αριθμό \(k\) ώστε \(ρ_1 < k < ρ_2\). Να βρείτε, με απόδειξη, το πρόσημο του αριθμού \(k^2-2λk+λ^2-1\).
(Mονάδες 6)

α) Παρατηρούμε ότι η εξίσωση είναι στην μορφή \(αx^2+βx+γ=0\) με \(α=1, β=-2λ, γ=λ^2-1\) και

\begin{align}Δ&=(-2λ)^2-4\cdot 1\cdot (λ^2-1)\\ &=4λ^2-4λ^2+4\\ &=4 > 0,\end{align}

άρα η διακρίνουσα \(Δ\) είναι πάντα θετική, ανεξάρτητα από την οποιαδήποτε τιμή της παραμέτρου \(λ\).

β) \(1^\text{ος}\) τρόπος:

\begin{align}ρ_{1,2}&=\frac{-β\pm\sqrt{Δ}}{2α}\\ &=\frac{-(-2λ)\pm\sqrt{4}}{2\cdot 1}\\ &=\frac{2λ\pm 2}{2}\\ &=\frac{2(λ\pm 1)}{2}\\ &=λ\pm 1.\end{align}

Ώστε \(ρ_1=λ-1, ρ_2=λ+1\).
\(2^\text{ος}\) τρόπος:
Η εξίσωση γράφεται:

\begin{align}&(x-λ)^2-1^2=0\\ \iff&(x-λ-1)(x-λ+1)=0\\ \iff&x-λ-1=0\text{ ή }x-λ+1=0\\ \iff&x=λ+1\text{ ή }x=λ-1.\end{align}

Έτσι \(ρ_1=λ-1, ρ_2=λ+1\) αφού \(ρ_1 < ρ_2\).

γ) Πρέπει

$$|ρ_2-(-ρ_1)|\geq 8\iff |ρ_1+ρ_2|\geq 8.$$

Αν έχουμε βρει τις ρίζες τότε \(ρ_1+ρ_2=2λ\). Χωρίς να βρούμε τις ρίζες, από τύπους Vieta,

$$ρ_1+ρ_2=-\frac{β}{α}=-\frac{-2λ}{1}=2λ.$$

Άρα, πρέπει

\begin{align}&|2λ|\geq 8\\ \iff&2|λ|\geq 8\\ \iff&|λ|\geq 2\\ \iff&λ\leq -2\text{ ή }λ\geq 2.\end{align}

δ) Έστω το τριώνυμο \(f(x)=1\cdot x^ 2-2λx+λ^2-1\) τις ρίζες του οποίου έχουμε βρει στο (β) ερώτημα.
Παρατηρούμε ότι:

$$k^2-2λk+λ^2-1=f(k) \lt 0,$$

σχέση που προκύπτει από τον παρακάτω πίνακα προσήμου του \(f(x)\).

α) Να λύσετε την ανίσωση \(x^2 > x\) στο σύνολο των πραγματικών αριθμών.
(Μονάδες 8)

β) Δίνεται ένας πραγματικός αριθμός \(α\) με \(α > 1\).
i. Να βάλετε στη σειρά, από τον μικρότερο στον μεγαλύτερο, τους αριθμούς:

$$0,\ 1,\ α,\ α^2,\ \sqrt{α}$$

αιτιολογώντας την απάντηση σας.
(Μονάδες 10)
ii. Να κάνετε το ίδιο για τους αριθμούς

$$α,\ α^2,\ \frac{α+α^2}{2}.$$

(Μονάδες 7)

α) Είναι:

$$x^2 > x\iff x^2-x > 0\quad (1)$$

Το τριώνυμο \(x^2-x=x(x-1)\) έχει ρίζες τις \(x=0, x=1\).
Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.

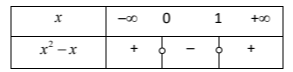
Επομένως η \((1)\) αληθεύει για \(x\in(-\infty, 0)\cup(1,+\infty)\).

β) i. Από τα δεδομένα και το (α) ερώτημα έχουμε

$$0 < 1 < α < α^2$$

και

$$1 < α\iff \sqrt{1} < \sqrt{α}\iff \sqrt{α} > 1.$$

Επίσης

$$α < α^2\iff \sqrt{α}<\sqrt{α^2}\overset{α > 0}\iff \sqrt{α} < α.$$

Οπότε τελικά

$$0 < 1 < \sqrt{α} < α < α^2.$$

ii. Έχουμε διαδοχικά:

\begin{align}&α < α^2\\ \iff&\frac{α}{2} < \frac{α^2}{2}\\ \iff&\frac{α}{2}+\frac{α}{2} < \frac{α^2}{2}+\frac{α}{2}\\ \iff&α < \frac{α^2+α}{2}.\end{align}

Επίσης:

\begin{align}&α < α^2\\ \iff&\frac{α}{2} < \frac{α^2}{2}\\ \iff&\frac{α^2}{2}+\frac{α}{2} < \frac{α^2}{2}+\frac{α^2}{2}\\ \iff&\frac{α^2+α}{2} < α^2.\end{align}

Οπότε τελικά:

$$α < \frac{α^2+α}{2} < α^2.$$

Δίνεται η ανίσωση

$$|x-1|\leq 3\quad (1).$$

α) Να λύσετε την ανίσωση \((1)\).
(Μονάδες 7)

β) Να βρείτε όλες τις ακέραιες λύσεις της ανίσωσης \((1)\).
(Μονάδες 3)

γ) Να βρείτε μία ανίσωση \(2^\text{ου}\) βαθμού που να έχει τις ίδιες ακριβώς λύσεις με την \((1)\).
(Μονάδες 8)

δ) Να δείξετε ότι αν το τετράγωνο ενός αριθμού ελαττωμένο κατά \(8\) δεν ξεπερνάει το διπλάσιό του, τότε η απόστασή του από το \(1\) δεν ξεπερνάει το \(3\).
(Μονάδες 7)

α) Είναι

\begin{align}&|x-1|\leq 3\\ \iff&-3\leq x-1\leq 3\\ \iff&-2\leq x\leq 4,\end{align}

δηλαδή \(x\in[-2,4]\).

β) Οι ακέραιες λύσεις στο διάστημα \([-2,4]\) είναι οι

$$-2,\ -1,\ 0,\ 1,\ 2,\ 3,\ 4.$$

γ) Αναζητούμε ένα τριώνυμο με ρίζες \(-2\) και \(4\) του οποίου το πρόσημο να είναι ετερόσημο του συντελεστή του δευτεροβάθμιου όρου.
Το άθροισμα των ριζών είναι \(S=-2+4=2\), το γινόμενο των ριζών είναι \(P=-2\cdot 4=-8\), οπότε ένα τριώνυμο είναι το

$$x^2-S\cdot x+P=x^2-2\cdot x-8$$

και αφού θέλουμε το πρόσημό του να είναι ετερόσημο του συντελεστή του δευτεροβάθμιου όρου, δηλαδή αρνητικό, έχουμε τελικά ότι η ζητούμενη ανίσωση είναι η

$$x^2-2x-8\leq 0.$$

δ) Έστω λοιπόν ένας αριθμός \(x\) του οποίου το τετράγωνο ελαττωμένο κατά \(8\) δεν ξεπερνάει το διπλάσιό του, δηλαδή

$$x^2-8\leq 2x\iff x^2-2x-8\leq 0.$$

Τότε όπως δείξαμε στο (γ) ερώτημα για αυτόν τον αριθμό \(x\) θα ισχύει ισοδύναμα ότι \(|x-1|\leq 3\), δηλαδή η απόστασή του από το \(1\) δεν ξεπερνάει το \(3\).

α) Δίνεται το τριώνυμο

$$x^2-3x+2,\ x\in\mathbb{R}.$$

Να βρείτε το πρόσημο του τριωνύμου.
(Μονάδες 10)

β) Θεωρούμε πραγματικούς αριθμούς \(α,\ β\) με \(α < β\) για τους οποίους ισχύει:

$$(α^2-3α+2)(β^2-3β+2) \lt 0.$$

i. Να αποδείξετε ότι οι αριθμοί \(α-1\) και \(β-2\) είναι ομόσημοι.
(Μονάδες 10)
ii. Να δείξετε ότι:

$$|(α-1)(β-2)|=(α-1)(β-2).$$

(Μονάδες 5)

α) Το τριώνυμο \(x^2-3x+2\) έχει \(α=1,\ β=-3,\ γ=2\) και διακρίνουσα:

$$Δ=β^2-4αγ=1 > 0.$$

Οι ρίζες του τριωνύμου είναι οι:

\begin{align}x_{1,2}&=\frac{-β\pm\sqrt{Δ}}{2α}\\ &=\frac{-(-3)\pm\sqrt{1}}{2\cdot 1}\\ &=\frac{3\pm 1}{2}\\ &=\begin{cases}\frac{3+1}{2}=2\\ \frac{3-1}{2}=1\end{cases}.\end{align}

Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.

Από τον πίνακα προσήμων συμπεραίνουμε ότι το τριώνυμο είναι θετικό για \(x\in(-\infty,1)\cup(2,+\infty)\) και αρνητικό για \(x\in(1, 2)\).

β) i. Δεδομένου ότι

$$(α^2-3α+2)(β^2-3β+2) < 0,$$

διακρίνουμε δυο περιπτώσεις:
\(1^\text{η}\) περίπτωση: \((α^2-3α+2) < 0\) και \((β^2-3β+2) > 0\).

Από το (α) ερώτημα \(α\in(1,2)\) και \(β\in(-\infty,1)\cup(2,+\infty)\), δηλαδή \(α > 1\) και αφού \(α < β\) θα είναι \(β > 2\), συνεπώς \(α-1\) και \(β-2\) είναι θετικοί, άρα ομόσημοι.

\(2^\text{η}\) περίπτωση: \((α^2-3α+2) > 0\) και \((β^2-3β+2) < 0\).
Από το (α) ερώτημα \(α\in(-\infty,1)\cup(2,+\infty)\) και \(β\in(1,2)\) δηλαδή \(β < 2\) και αφού \(α < β\), θα είναι \(α < 1\), συνεπώς \(α-1\) και \(β-2\) είναι αρνητικοί άρα ομόσημοι.

ii. Αφού \(α-1\) και \(β-2\) είναι ομόσημοι, έχουμε ότι \((α-1)(β-2) > 0\), οπότε:

$$|(α-1)(β-2)|=(α-1)(β-2).$$

α) Να βρείτε το πρόσημο του τριωνύμου \(x^2-x-12\) για τις διάφορες τιμές του \(x\in \mathbb{R}\).
(Μονάδες 8)

β) Να δείξετε ότι

$$\left(\frac{π+9}{3}\right)^2-\left(\frac{π+9}{3}\right)-12 > 0,$$

όπου \(π=3,1415\dots\;\).
(Μονάδες 9)

γ) Αν για τον πραγματικό αριθμό \(α\) ισχύει ότι

$$(|α|+3)^2-(|α|+3)-12 < 0,$$

να δείξετε ότι \(α\in (-1,1)\).
(Μονάδες 8)

α) Το τριώνυμο \(x^2-x-12\) έχει

$$Δ=1-4\cdot (-12)=1+48=49$$

και δύο ρίζες άνισες, τις

$$x_1=\frac{-(-1)+\sqrt{49}}{2\cdot 1}=\frac{1+7}{2}=\frac{8}{2}=4$$

και

$$x_2=\frac{-(-1)-\sqrt{49}}{2\cdot 1}=\frac{1-7}{2}=\frac{-6}{2}=-3.$$

Το πρόσημο του τριωνύμου \(x^2-x-12\) φαίνεται στον παρακάτω πίνακα

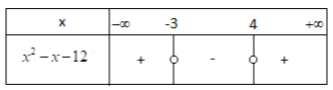
Δηλαδή \(x^2-x-12 < 0\) για κάθε \(x\in(-3,4)\) και \(x^2-x-12 > 0\) για κάθε \(x\in(-\infty,-3)\cup(4,+\infty)\).

β) Είναι

$$π > 3\iff π+9 > 12\iff \frac{π+9}{3} > 4,$$

οπότε με βάση το (α) έχουμε ότι

$$\left(\frac{π+9}{3}\right)^2-\left(\frac{π+9}{3}\right)-12 > 0.$$

γ) Η παράσταση \((|α|+3)^2-(|α|+3)-12\) είναι η τιμή του τριωνύμου για \(x=|α|+3\) και για να είναι αρνητική θα πρέπει:

\begin{align}&-3 < |α|+3 < 4\\ \iff&-6 < |α| < 1\\ \iff&|α| < 1\\ \iff&-1 < α < 1\\ \iff&α\in(-1,1).\end{align}

Δίνεται η εξίσωση \(|x-4|-|x-2|=2\).

α) Να διατυπώσετε γεωμετρικά το ζητούμενο της παραπάνω εξίσωσης.
(Μονάδες 8)

β) Να αιτιολογήσετε γεωμετρικά ότι οι λύσεις της παραπάνω εξίσωσης είναι όλοι οι πραγματικοί αριθμοί που ανήκουν στο \((-∞,2]\) και μόνο αυτοί.
(Μονάδες 8)

γ) Αν για τον πραγματικό αριθμό \(x\) ισχύει ότι \(|x-4|-|x-2|=2\), τότε να δείξετε ότι \(x^{2}-6x+8≥0\).
(Μονάδες 9)

ΛΥΣΗ

α) Αναζητούμε πραγματικούς αριθμούς \(x\) των οποίων η απόσταση από το \(4\) είναι δύο μονάδες μεγαλύτερη από την απόστασή τους από το \(2\). Δηλαδή:

$$d(x,4)-d(x,2)=2$$

β) Έστω ότι τα σημεία \(Μ\), \(Α\), \(Β\) αναπαριστούν στον άξονα των πραγματικών αριθμών, τους αριθμούς \(x\), \(2\), \(4\) αντίστοιχα, όπως φαίνεται στα παρακάτω σχήματα.

Παρατηρούμε ότι \(d(2,4)=(ΑΒ)=2\).

Για κάθε αριθμό \(x∈(-∞,2]\) είναι \(d(x,4)-d(x,2)=(ΜΒ)-(ΜΑ)=(ΑΒ)=2\).

Για κάθε αριθμό \(x∈(2,4]\) είναι:

$$d(x,4)-d(x,2) < d(x,4)+d(x,2)$$ $$=(ΜΒ)+(ΜΑ)=(ΑΒ)=2$$

και άρα:

$$d(x,4)-d(x,2)≠2$$

Για κάθε αριθμό \(x∈(4,+∞)\) είναι \((ΜΒ)<(ΜΑ)\) οπότε \(d(x,4)<d(x,2)\) δηλαδή \(d(x,4)-d(x,2)<0\) και άρα \(d(x,4)-d(x,2)≠2\).

γ) όπως δείξαμε στο β), αν για τον πραγματικό αριθμό ισχύει \(x\) ότι \(|x-4|-|x-2|=2\), τότε \(x∈(-∞,2]\).

Το τριώνυμο \(x^{2}-6x+8\) έχει ρίζες τους αριθμούς \(2\) και \(4\) και γίνεται μη αρνητικό για \(x∈(-∞,2]∪[4,+∞)\).

Συνεπώς αν για τον πραγματικό αριθμό \(x\) ισχύει ότι \(|x-4|-|x-2|=2\), τότε \(x∈(-∞,2]\) και \(x^{2}-6x+8≥0\).

α) Θεωρούμε την εξίσωση \(x^{2}+2x+3=α\), με παράμετρο \(α\in \mathbb{R}\).

1. Να βρείτε για ποιες τιμές του \(α\) η εξίσωση \(x^{2}+2x+3=α\) έχει δύο πραγματικές και άνισες ρίζες.
   (Μονάδες 6)

2. Να βρείτε την τιμή του \(α\) ώστε η εξίσωση να έχει μια διπλή ρίζα, την οποία και να προσδιορίσετε.
   (Μονάδες 6)

β) Δίνεται η συνάρτηση \(f(x)=x^{2}+2x+3\), \(x\in \mathbb{R}\).

1. Να αποδείξετε ότι \(f(x)\ge 2\) για κάθε \(x\in \mathbb{R}\).
   (Μονάδες7)

2. Να λύσετε την ανίσωση \(\sqrt{f(x)-2}\le 2\).
   (Μονάδες 6)

ΛΥΣΗ

α) Η εξίσωση \(x^{2}+2x+3=α\) ισοδύναμα γράφεται:

$$x^{2}+2x+3-α=0\ \ \ \ (1)$$

και έχει διακρίνουσα:

$$Δ=β^{2}-4αγ=2^{2}-4\cdot 1\cdot (3-α)=$$ $$=4-12+4α=4α-8$$

1. Η εξίσωση \((1)\) έχει δύο ρίζες πραγματικές και άνισες αν και μόνο αν:

$$Δ>0 $$ $$\Leftrightarrow 4α-8>0 $$ $$\Leftrightarrow 4α>8 $$ $$\Leftrightarrow α>2$$

2. Η εξίσωση \((1)\) έχει μια διπλή ρίζα αν και μόνο αν:

   $$Δ=0 $$ $$\Leftrightarrow 4α-8=0 $$ $$\Leftrightarrow 4α=8 $$ $$\Leftrightarrow α=2$$

   Για \(α=2\) η διπλή ρίζα είναι η:

   $$x=\dfrac{-β}{2α}$$ $$=\dfrac{-2}{2}=-1$$

β)

1. Είναι:

   $$f(x)\ge 2 $$ $$\Leftrightarrow x^{2}+2x+3\ge 2 $$ $$\Leftrightarrow x^{2}+2x+1\ge 0 $$ $$\Leftrightarrow (x+1)^{2}\ge 0$$

   το οποίο ισχύει για κάθε \(x\in \mathbb{R}\).

2. Από το ερώτημα β)i. έχουμε ότι:

   $$f(x)\ge 2 $$ $$\Leftrightarrow f(x)-2\ge 0$$

   για κάθε \(x\in \mathbb{R}\). Οπότε ισοδύναμα έχουμε:

   $$\sqrt{f(x)-2}\le 2 $$ $$\Leftrightarrow (\sqrt{f(x)-2})^{2}\le 2^{2} $$ $$\Leftrightarrow f(x)-2\le 4 $$ $$\Leftrightarrow f(x)\le 6 $$ $$\Leftrightarrow x^{2}+2x+3\le 6 $$ $$\Leftrightarrow x^{2}+2x-3\le 0$$

   Το τριώνυμο έχει διακρίνουσα:

   $$Δ=β^{2}-4αγ$$ $$=2^{2}-4\cdot 1\cdot (-3)$$ $$=4+12=16>0$$

   και ρίζες τις:

   $$x_{\text{1,2}}=\dfrac{-β\pm \sqrt{Δ}}{2α}$$ $$=\dfrac{-2\pm \sqrt{16}}{2}$$ $$=\begin{cases} \dfrac{-2+4}{2}=1 \\ \dfrac{-2-4}{3}=-3 \end{cases}$$

   Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα:

   

   Από τον πίνακα προσήμων συμπεραίνουμε ότι:

   $$x^{2}+2x-3\le 0 $$ $$\Leftrightarrow -3\le x\le 1 $$ $$\Leftrightarrow x\in [-3,1]$$

α) Να λύσετε την ανίσωση:

$$x^{2}+1\ge \dfrac{5}{2}x\ \ \ \ (1)$$

(Μονάδες10)

β) Δίνονται δύο αριθμοί \(κ\), \(λ\) οι οποίοι είναι λύσεις της ανίσωσης \((1)\) και ικανοποιούν επιπλέον τη σχέση \((λ-1)(κ-1)<0\).

1. Να δείξετε ότι το \(1\) είναι μεταξύ των αριθμών \(κ\), \(λ\).
   (Μονάδες 8)

2. Να δείξετε ότι \(|κ-λ|\ge \dfrac{3}{2}\).
   (Μονάδες 7)

ΛΥΣΗ

α) Έχουμε

$$x^{2}+1\ge \dfrac{5}{2}x $$ $$\Leftrightarrow 2x^{2}-5x+2\ge 0$$

Tο τριώνυμο \(2x^{2}-5x+2\) έχει διακρίνουσα

$$Δ=(-5)^{2}-4\cdot 2\cdot 2=9>0$$

και ρίζες

$$x_{1}=\dfrac{-(-5)-\sqrt{9}}{2\cdot 2}$$ $$=\dfrac{5-3}{4}=\dfrac{2}{4}=\dfrac{1}{2}$$

$$x_{2}=\dfrac{-(-5)+\sqrt{9}}{2\cdot 2}$$ $$=\dfrac{5+3}{4}=\dfrac{8}{4}=2$$

Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα

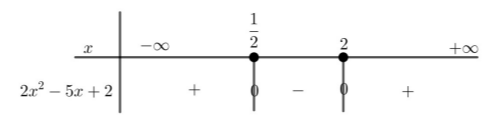
Άρα η ανίσωση \((1)\) αληθεύει για \(x\in \left( -\infty ,\dfrac{1}{2} \right] \cup [2,+\infty )\).

β) Επειδή \((λ-1)(κ-1)<0\), οι αριθμοί \(λ-1\) και \(κ-1\) είναι ετερόσημοι.

1. Αν

$$\begin{cases} λ-1>0 \\ \text{και} \\ κ-1<0 \end{cases} $$ $$\Leftrightarrow \begin{cases} λ>1 \\ \text{και} \\ κ<1 \end{cases}$$

τότε

$$κ<1<λ$$

Αν

$$\begin{cases} λ-1<0 \\ \text{και} \\ κ-1>0 \end{cases} $$ $$\Leftrightarrow \begin{cases} λ<1 \\ \text{και} \\ κ>1 \end{cases}$$

τότε

$$λ<1<κ$$

Σε κάθε περίπτωση, το \(1\) είναι μεταξύ των αριθμών \(κ\), \(λ\).

2. Οι αριθμοί \(κ\), \(λ\) είναι λύσεις της ανίσωσης \((1)\) και το \(1\) είναι μεταξύ τους.
   Άρα

$$\begin{cases} κ\le \dfrac{1}{2} \\ \text{και} \\ λ\ge 2 \end{cases} $$ $$\Leftrightarrow \begin{cases} κ\le \dfrac{1}{2} \\ \text{και} \\ -λ\le -2 \end{cases}$$

οπότε

$$κ-λ\le \dfrac{1}{2}-2 $$ $$\Leftrightarrow κ-λ\le -\dfrac{3}{2}$$

ή

$$\begin{cases} λ\le \dfrac{1}{2} \\ \text{και} \\ κ\ge 2 \end{cases} $$ $$\Leftrightarrow \begin{cases} -λ\ge -\dfrac{1}{2} \\ \text{και} \\ κ\ge 2 \end{cases}$$

οπότε

$$κ-λ\ge 2-\dfrac{1}{2} $$ $$\Leftrightarrow κ-λ\ge \dfrac{3}{2}$$

Τελικά

$$|κ-λ|\ge \dfrac{3}{2}$$

α) Να λύσετε την ανίσωση \(x^{2}-4x+3<0\ \ \ \ (1)\).
(Μονάδες 13)

β) Αν η \((1)\) έχει λύσεις τους αριθμούς \(x\) για τους οποίους ισχύει \(1<x<3\) και οι αριθμοί \(α\), \(β\) είναι λύσεις της ανίσωσης \((1)\), να δείξετε ότι και ο αριθμός \(\dfrac{α+β}{2}\) είναι επίσης λύση της ανίσωσης \((1)\).
(Μονάδες 12)

ΛΥΣΗ

α) Το τριώνυμο \(x^{2}-4x+3\) έχει διακρίνουσα:

$$Δ=(-4)^{2}-4\cdot 1\cdot 3$$ $$=16-12=4$$

και ρίζες:

$$x_{\text{1,2}}=\dfrac{-(-4)\pm \sqrt{4}}{2\cdot 1}$$ $$=\dfrac{4\pm 2}{2}$$ $$=\begin{cases} \dfrac{4+2}{2}=3 \\ \dfrac{4-2}{2}=1 \end{cases}$$

Το πρόσημο του τριωνύμου για τις διάφορες τιμές του \(x\) φαίνεται στον παρακάτω πίνακα:

Από τον πίνακα προσήμων συμπεραίνουμε ότι:

$$x^{2}-4x+3 < 0 $$ $$\Leftrightarrow 1 < x < 3 $$

β) Για να είναι ο \(\dfrac{α+β}{2}\) λύση της ανίσωσης \((1)\) αρκεί να δείξουμε \(1<\dfrac{α+β}{2}<3\).

Έχουμε ότι:

$$\left. \array { 1<α<3 \cr 1<β<3 } \right\} \overset{(+)}{\Rightarrow} 2<α+β<6 $$ $$\overset{(:2)}{\Rightarrow} 1<\dfrac{α+β}{2}<3$$

α) Να αποδείξετε ότι \(x^{2}+4x+5>0\), για κάθε πραγματικό αριθμό \(x\).
(Μονάδες 10)

β) Να γράψετε χωρίς απόλυτες τιμές την παράσταση:

$$Β=|x^{2}+4x+5|-|x^{2}+4x+4|$$

(Μονάδες 15)

ΛΥΣΗ

α) Το τριώνυμο \(x^{2}+4x+5\) έχει \(α=1\), \(β=4\), \(γ=5\) και διακρίνουσα:

$$Δ=β^{2}-4αγ=4^{2}-4\cdot 1\cdot 5$$ $$=16-20=-4 < 0$$

Επειδή \(α=1>0\), ισχύει ότι: \(x^{2}+4x+5>0\) για κάθε πραγματικό αριθμό \(x\).

β) Είναι:

$$x^{2}+4x+4=(x+2)^{2}\ge 0$$

Τότε:

$$Β=|x^{2}+4x+5|-|x^{2}+4x+4| $$ $$\overset{(α)}{\Leftrightarrow} Β=x^{2}+4x+5-(x^{2}+4x+4) $$ $$\Leftrightarrow Β=x^{2}+4x+5-x^{2}-4x-4 $$ $$\Leftrightarrow B=1$$

Δίνεται το τριώνυμο \(f(x)=3x^{2}+9x-12\), \(x\in \mathbb{R}\).

α) Να λύσετε την ανίσωση \(f(x)\le 0\) και να παραστήσετε το σύνολο των λύσεων της στον άξονα των πραγματικών αριθμών.
(Μονάδες 13)

β) Να ελέγξετε αν ο αριθμός \(\sqrt[3]{2}\) είναι λύση της ανίσωσης του α) ερωτήματος. Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 12)

ΛΥΣΗ

α) Το τριώνυμο \(f(x)=3x^{2}+9x-12\) έχει \(α=3\), \(β=9\), \(γ=-12\) και διακρίνουσα:

$$Δ=β^{2}-4αγ$$ $$=9^{2}-4\cdot 3\cdot (-12)$$ $$=81+144=225>0$$

Οι ρίζες του τριωνύμου είναι:

$$x_{\text{1,2}}=\dfrac{-β\pm \sqrt{Δ}}{2α}$$ $$=\dfrac{-9\pm \sqrt{225}}{2\cdot 3}$$ $$=\dfrac{-9\pm 15}{6}$$ $$=\begin{cases} \dfrac{-9+15}{6}=1 \\ \dfrac{-9-15}{6}=-4 \end{cases}$$

Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα:

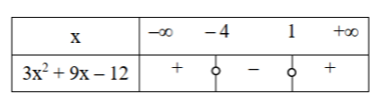
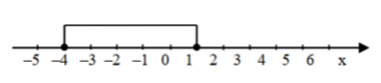
Επομένως ισχύει:

$$f(x)\le 0 $$ $$\Leftrightarrow 3x^{2}+9x-12\le 0 $$ $$\Leftrightarrow -4\le x\le 1 $$ $$\Leftrightarrow x\in [-4,1]$$

β) Ο αριθμός \(\sqrt[3]{2}\) είναι λύση της ανίσωσης αν και μόνο αν:

$$-4\le \sqrt[3]{2}\le 1 $$ $$\Leftrightarrow \sqrt[3]{2}\le 1 $$ $$\Leftrightarrow (\sqrt[3]{2})^{3}\le 1^{3} $$ $$\Leftrightarrow 2\le 1$$

Το οποίο δεν ισχύει. Άρα ο αριθμός \(\sqrt[3]{2}\) δεν είναι λύση της ανίσωσης.