Μάθημα : Α΄ΛΥΚΕΙΟΥ - ΑΛΓΕΒΡΑ

Έστω \(α, β\) πραγματικοί αριθμοί για τους οποίους ισχύουν:

$$α+β=2 \text{ και } α^{2} \cdot β + α \cdot β^{2}=-30$$

α) Να αποδείξετε ότι: \(α \cdot β = -15.\)
(Μονάδες 10)

β) Να κατασκευάσετε εξίσωση δευτέρου βαθμού με ρίζες τους αριθμούς \(α, β\) και να τους βρείτε.
(Μονάδες 15)

α) Είναι:

$$\begin{align} α^{2} β + α β^{2} & = - 30 \\ αβ(α+β) & = - 30 \\ αβ \cdot 2 & = - 30 \\ αβ & = - 15\end{align}$$

β) Η ζητούμενη εξίσωση είναι της μορφής:

$$x^{2} - Sx + P = 0$$ $$\text{με } S = α + β = 2 \text{ και } Ρ = αβ = - 15$$

Τελικά η ζητούμενη εξίσωση είναι η: \(x^{2} - 2x - 15 = 0.\)

Το τριώνυμο \(x^{2} - 2x - 15\) έχει διακρίνουσα:
\(Δ = β^{2} - 4αγ\)
\(= (-2)^{2} - 4 \cdot 1 \cdot (-15)\)
\(= 4+60 = 64 > 0\)

Οι ρίζες της εξίσωσης είναι:

$$x_{1,2} = \dfrac{−β± \sqrt{Δ}}{2α}$$ $$=\dfrac{−(−2)±\sqrt{64}}{2 \cdot 1}$$ $$=\dfrac{2±8}{2}$$ $$\left\{\begin{array}{ll} x_{1}=\dfrac{2+8}{2}=5 \\ x_{2}=\dfrac{2-8}{2}=-3 \end{array} \right.$$

Άρα είναι:

$$(α = 5 \text{ και } β = - 3)$$ $$\text{ή } (α = - 3 \text{ και } β = 5)$$

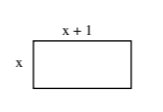
Το πάτωμα του εργαστήριου της πληροφορικής ενός σχολείου είναι σχήματος ορθογωνίου με διαστάσεις \((x+1)\) μέτρα και \(x\) μέτρα.

α) Να γράψετε με τη βοήθεια του \(x\) την περίμετρο και το εμβαδόν του πατώματος.
(Μονάδες 10)

β) Αν το εμβαδόν του πατώματος του εργαστηρίου είναι \(90\) τετραγωνικά μέτρα, να βρείτε τις διαστάσεις του.
(Μονάδες 15)

α) Η περίμετρος \(Π\) του ορθογωνίου είναι:
\(Π = 2(x + 1) + 2x = 4x + 2, \text{ με } x > 0\)
και το εμβαδόν του \(Ε\) είναι:
\(Ε = x(x + 1) = x^{2} + x, \text{ με } x > 0\)

β) Ισχύει ότι:

$$Ε = 90 $$ $$x^{2} + x = 90$$ $$x^{2} + x - 90=0$$

Το τριώνυμο \(x^{2} + x - 90\) έχει \(α = 1, β = 1, γ = - 90\) και διακρίνουσα: \(Δ = β^{2} - 4 \cdot α \cdot γ = 1^{2} - 4 \cdot 1 \cdot (- 90) = 361 > 0.\)

Οι ρίζες της εξίσωσης \(x^{2} + x - 90 = 0\) είναι:

$$x_{1,2}=\dfrac{-β±\sqrt{Δ}}{2α}$$ $$\dfrac{-1±\sqrt{361}}{2 \cdot 1}$$ $$\dfrac{-1±19}{2}$$ $$\left \{ \begin{array}{ll} x_{1}=\dfrac{-1+19}{2}=9 \\ x_{2}=\dfrac{-1-19}{2}=-10, \text{ απορ. } (x>0) \end{array} \right.$$

Άρα οι διαστάσεις του ορθογωνίου είναι: \(x = 9\) μέτρα και \(x + 1 = 10\) μέτρα.

Δίνεται η εξίσωση \(x^2-(λ-1)x+6=0, \quad (1)\) με παράμετρο \(λ \in \mathbb{ℝ}.\)

α) Αν η παραπάνω εξίσωση έχει λύση το \(1\), να βρείτε το \(λ\).
(Μονάδες 13)

β) Για \(λ=2\) να λύσετε την εξίσωση \((1)\).
(Μονάδες 12)

α) Αφού η εξίσωση \((1)\) έχει λύση το \(1\), ισχύει ότι:

$$1^2 - (λ - 1) \cdot 1 + 6 = 0$$ $$1 - λ + 1 + 6 = 0$$ $$8 - λ = 0$$ $$λ = 8$$

β) Για \(λ = 2\) η εξίσωση γράφεται:

$$x^2 - (2 - 1)x + 6 = 0$$ $$x^2 - x + 6 = 0$$

Για \(α = 1, \ β = - 1\) και \(γ = 6\), βρίσκουμε:

$$\begin{align}Δ &= β^2 - 4αγ \\ &= (- 1)^2 - 4 \cdot 1 \cdot 6 \\ & = 1 - 24 \\ & = - 23 \lt 0 \end{align}$$

Άρα η εξίσωση δεν έχει πραγματικές ρίζες.

α) Να λύσετε την εξίσωση \(|x-2|=\sqrt{3}\).
(Μονάδες 10)

β) Να σχηματίσετε εξίσωση δευτέρου βαθμού με ρίζες, τις ρίζες της εξίσωσης του (α) ερωτήματος.
(Μονάδες 15)

α) Είναι:

\begin{align}&|x - 2| = \sqrt{3}\\ \iff&(x - 2 = \sqrt{3} \text{ ή } x - 2 = - \sqrt{3})\\ \iff&(x = 2 + \sqrt{3} \text{ ή } x = 2 - \sqrt{3})\end{align}

β) Η ζητούμενη εξίσωση είναι της μορφής:

$$x^2 - Sx + P = 0$$

με

\begin{align}S &= x_1 + x_2 \\ &= 2 + \sqrt{3} + 2 - \sqrt{3} \\ &= 4\end{align}

και

\begin{align}Ρ &= x_1x_2 \\ &= (2 + \sqrt{3})(2 - \sqrt{3}) \\ &= 2^2 - \sqrt{3}^2 \\ &= 4 - 3 =1\end{align}

Τελικά η ζητούμενη εξίσωση είναι η:

$$x^2 - 4x + 1 = 0$$

Δίνεται η εξίσωση

$$αx^2-2αx-2α-2=0,\text{ με }α\in\mathbb{R}^*\quad (1).$$

α) Να βρείτε τις τιμές του \(α\in\mathbb{R}^*\) για τις οποίες η εξίσωση \((1)\) έχει ρίζα το \(3\).
(Μονάδες 10)

β) Για \(α=2\) να λύσετε την εξίσωση \((1)\).
(Μονάδες 15)

α) Για \(x=3\) η εξίσωση \((1)\) γίνεται:

\begin{align}&α\cdot 3^2-2α\cdot 3-2α−2=0\\ \iff&9α-6α-2α-2=0\\ \iff&α=2.\end{align}

Άρα \(α=2\).

β) Στη σχέση \((1)\) αντικαθιστούμε το \(α=2\) και προκύπτει η δευτεροβάθμια εξίσωση \(2x^2-4x-6=0 \Leftrightarrow x^2-2x-3=0\), με \(α=1,\ β=-2\) και \(γ=-3\).
Το τριώνυμο έχει διακρίνουσα

$$Δ=2^2-4\cdot(-3)\cdot1=16 > 0$$

οπότε έχει δύο άνισες ρίζες

$$x_1=\frac{-(-2)+4}{2}=3$$

και

$$x_2=\frac{-(-2)-4}{2}=-1.$$

Άρα η εξίσωση έχει λύσεις \(x=-1\) ή \(x=3\).

Οι αριθμοί \(1,3,6,10,\dots\) και γενικά αυτοί που είναι δυνατόν, αν παρασταθούν με τελείες, να τοποθετηθούν σε μια τριγωνική διάταξη της μορφής που φαίνεται στον παρακάτω πίνακα λέγονται τριγωνικοί.

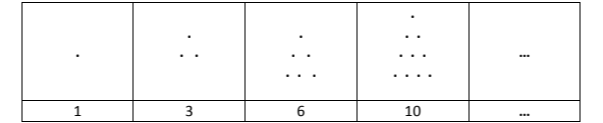
Αποδεικνύεται ότι ο νιοστός τριγωνικός αριθμός δίνεται από τον τύπο

$$T_ν=\frac{ν(ν+1)}{2},\ ν\in\mathbb{N}^*$$

α) Να βρείτε τον \(10^ο\) τριγωνικό αριθμό.
(Μονάδες 6)

β) Να εξετάσετε αν ο αριθμός \(120\) είναι τριγωνικός.
(Μονάδες 9)

γ) Να αποδείξετε ότι το άθροισμα δυο διαδοχικών τριγωνικών αριθμών είναι ίσο με το τετράγωνο θετικού ακεραίου.
(Μονάδες 10)

α) Ο δέκατος τριγωνικός αριθμός είναι

$$T_{10}=\frac{10\cdot 11}{2}=55$$

β) Ο αριθμός \(120\) είναι τριγωνικός μόνο όταν η εξίσωση \(T_ν=120\) έχει λύση θετικό ακέραιο αριθμό. Είναι:

\begin{align}&T_ν=120\\ \iff&\frac{ν(ν+1)}{2}=120\\ \iff&ν(ν+1)=240\\ \iff&ν^2+ν-240=0\end{align}

Η διακρίνουσα της εξίσωσης είναι \(Δ=961\) και οι ρίζες της

$$ν_{1,2}=\frac{-1\pm 31}{2}=\begin{cases}ν_1=\frac{30}{2}=15\\ν_2=-\frac{32}{2}=-16\end{cases}$$

Από τις ρίζες της εξίσωσης δεκτή είναι μόνο ο αριθμός \(15\). Άρα ο αριθμός \(120\) είναι ο δέκατος πέμπτος τριγωνικός αριθμός \((T_{15}=120)\).

γ) Έστω \(T_ν,T_{ν+1}\) δυο διαδοχικοί τριγωνικοί αριθμοί με \(ν\) θετικό ακέραιο. Τότε έχουμε:

\begin{align}T_ν+T_{ν+1}&=\frac{ν(ν+1)}{2}+\frac{(ν+1)(ν+2)}{2}\\ &=\frac{1}{2}(ν+1)(ν+ν+2)\\ &=\frac{1}{2}(ν+1)\cdot 2(ν+1)\\ &=(ν+1)^2\end{align}

οπότε το άθροισμα δυο διαδοχικών τριγωνικών αριθμών είναι ίσο με το τετράγωνο θετικού ακεραίου.

Δίνονται οι μη μηδενικοί πραγματικοί αριθμοί \(α, β\), με \(α\neq β\) για τους οποίους ισχύει:

$$\frac{α^2+1}{β^2+1}=\frac{α}{β}.$$

α) Να αποδείξετε ότι οι αριθμοί \(α\) και \(β\) είναι αντίστροφοι.
(Μονάδες 5)

β) Να υπολογίσετε την τιμή της παράστασης

$$Κ=\frac{α^{22}\cdot(β^3)^8}{α^{-2}\cdot(αβ)^{25}}.$$

(Μονάδες 7)

γ) Αν επιπλέον οι μη μηδενικοί αριθμοί \(α\) και \(β\) εκφράζουν τα μήκη των πλευρών ορθογωνίου παραλληλογράμμου με άθροισμα \(\frac{5}{2}\), να τους υπολογίσετε.
(Μονάδες 8)

δ) Να βρείτε τον αριθμό που πρέπει να προσθέσετε στο \(α\) ή στο \(β\), έτσι ώστε το ορθογώνιο παραλληλόγραμμο να γίνει τετράγωνο.
(Μονάδες 5)

α) Η δοθείσα ισότητα ισοδύναμα γράφεται:

\begin{align}&\frac{α^2+1}{β^2+1}=αβ\\ \iff&β\cdot (α^2 + 1)=α\cdot (β^2 + 1)\\ \iff&α^2\cdot β+β=α\cdot β^2+α\\ \iff&α^2\cdot β+β-α\cdot β^2-α=0\\ \iff&α\cdot β\cdot (α-β)-(α-β)=0\\ \iff&(α-β)\cdot (α\cdot β-1)=0\\ \overset{α\neq β}{\iff}&α\cdot β-1=0\\ \iff&α\cdot β=1.\end{align}

Άρα οι αριθμοί \(α, β\) είναι αντίστροφοι.
β) Η παράσταση γράφεται:

\begin{align}Κ&=\frac{α^{22}\cdot (β^3)^8}{α^{-2}\cdot (αβ)^{25}}\\ &=\frac{α^{22}\cdot β^{24}}{α^{-2}\cdot α^{25}\cdot β^{25}}\\ &=\frac{α^{22}\cdot β^{24}}{α^{23}\cdot β^{25}}\\ &=\frac{α^{22}}{α^{23}}\cdot \frac{β^{24}}{β^{25}}\\ &=\frac{1}{α}\cdot \frac{1}{β}\\ &=\frac{1}{αβ}\\ &=1.\end{align}

γ) Γνωρίζουμε πως \(α+β=\frac{5}{2}\) και \(α\cdot β=1\) με \(α,β>0\). Σύμφωνα με τους τύπους Vieta, αν

$$s=α+β$$

και

$$p=α\cdot β,$$

προκύπτει ότι οι αριθμοί \(α, β\) είναι ρίζες της δευτεροβάθμιας εξίσωσης

\begin{align}&x^2-s𝑥+p=0\\ \iff&x^2-\frac{5}{2}x+1=0\\ \iff&2x^2-5x+2=0.\end{align}

Η διακρίνουσα του τριωνύμου είναι:

$$Δ=(-5)^2-16=9$$

και οι ρίζες:

\begin{align}&x_{1,2}=\frac{5\pm 3}{4}\\ \iff&x_1=2\text{ ή }x_2=\frac{1}{2}.\end{align}

Άρα, οι ζητούμενοι αριθμοί είναι \(α=2\) και \(β=\frac{1}{2}\) ή αντίστροφα.

δ) Από το προηγούμενο ερώτημα θεωρούμε \(α=2\) και \(β=\frac{1}{2}\). Για να είναι το σχήμα τετράγωνο πρέπει τα μήκη των πλευρών του ορθογωνίου παραλληλογράμμου να γίνουν ίσα.

Έστω \(ω\) ο αριθμός που θα προσθέσουμε στον μικρότερο που είναι ο \(β\) για να γίνει ίσο με το \(α\), τότε:

\begin{align}&α=β+ω\\ \iff&2=\frac{1}{2}+ω\\ \iff&ω=\frac{3}{2}.\end{align}

Άρα, πρέπει να προστεθεί στο \(β\) ο αριθμός \(\frac{3}{2}\).

Έστω \(Ω\) το σύνολο που έχει ως στοιχεία τους αριθμούς που είναι οι ενδείξεις ενός ζαριού.

α) Να γράψετε με αναγραφή το σύνολο \(Ω\).
(Μονάδες 5)

β) Δίνεται η εξίσωση

$$x^2-2x+λ-2=0,\ λ\in\mathbb{R}.$$

Να βρείτε:
i. Το σύνολο \(Α\) που περιέχει ως στοιχεία τις τιμές του \(λ\in Ω\), αν επιπλέον γνωρίζετε ότι η εξίσωση δεν έχει πραγματικές ρίζες.
(Μονάδες 10)
ii. Την πραγματική τιμή του \(λ\), αν η εξίσωση έχει ρίζες αντίστροφες.
(Μονάδες 6)

γ) Για την τιμή του \(λ\) που βρήκατε στο ερώτημα (β.ii) να υπολογίσετε τις ρίζες της εξίσωσης.
(Μονάδες 4)

α) Οι ενδείξεις ενός ζαριού είναι οι ακέραιες τιμές από το \(1\) ως το \(6\).
Άρα, \(Ω=\{1,2,3,4,5,6\}\).

β) i. Η εξίσωση \(x^2-2x+λ-2=0\) ως δευτεροβάθμια δεν έχει πραγματικές ρίζες όταν \(Δ < 0\). Έχουμε

\begin{align}Δ&=(-2)^2-4\cdot 1\cdot (λ-2)\\ &=4-4\cdot λ+8\\ &=12-4\cdot λ.\end{align}

Άρα:

\begin{align}&Δ < 0\\ \iff&12-4\cdot λ < 0\\ \iff&λ > 3\\ \iff&λ\in(3,+\infty),\end{align}

ενώ επιπλέον \(λ\in Ω=\{1,2,3,4,5,6\}\).
Τελικά προκύπτει \(λ=4\) ή \(5\) ή \(6\).

Άρα το ζητούμενο σύνολο είναι \(Α=\{4,5,6\}\).
ii. Έστω \(x_1\) και \(x_2\) οι ρίζες της εξίσωσης με \(x_1\cdot x_2=1\).
Σύμφωνα με τους τύπους Vieta

$$x_1\cdot x_2=\frac{α}{γ}=λ-2,$$

άρα

$$x_1\cdot x_2=1\iff λ-2=1\iff λ=3.$$

γ) Για \(λ=3\) η εξίσωση γίνεται:

\begin{align}&x^2-2x+1=0\\ \iff&(x-1)^2=0\\ \iff&x=1\text{ (διπλή ρίζα)}.\end{align}

Άρα, η ρίζα της εξίσωσης είναι η \(x=1\) (διπλή).

Κάθε περιττός ακέραιος αριθμός \(α\) γράφεται στη μορφή \(α=2k+1,\ k\) ακέραιος.

α) Να γράψετε τους αριθμούς \(3,\ 5,\ 7\) ως διαφορά τετραγώνων δύο ακεραίων.
(Μονάδες 6)

β) i) Να αποδείξετε ότι η διαφορά των τετραγώνων δύο διαδοχικών ακεραίων ισούται πάντα με έναν περιττό ακέραιο.
(Μονάδες 6)
ii) Να γράψετε τον αριθμό \(2021\) ως διαφορά δύο τετραγώνων ακεραίων αριθμών.
(Μονάδες 6)

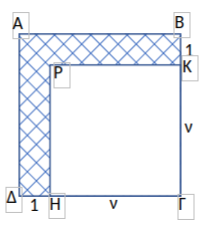
γ) Στο σχήμα τα τετράπλευρα \(ΑΒΓΔ\) και \(ΓΗΡΚ\) είναι τετράγωνα με \((ΓΗ)=(ΓΚ)=ν\) και \((ΒΚ)=(ΔΗ)=1\). Αν γνωρίζουμε ότι το γραμμοσκιασμένο εμβαδόν είναι ίσο με το εμβαδόν ενός τετραγώνου πλευράς \(45\), να βρεθεί η τιμή του θετικού ακεραίου \(ν\).
(Μονάδες 7)

α) Έχουμε διαδοχικά \(3=4-1=2^2-1^2\), \(5=3^2-2^2\) και σκεπτόμενοι ότι \(7=Μ^2-Ν^2=(Μ-Ν)(Μ+Ν)\), ένα γινόμενο ακεραίων που δίνει \(7\) είναι οι \(1, 7\). Αν \(Μ>Ν\) τότε \(Μ-Ν=1, Μ+Ν=7\) και λύνοντας το σύστημα έχουμε με αντικατάσταση \(Μ=Ν+1\) και \(Ν+1+Ν = 7\), άρα \(2Ν = 6\), δηλαδή \(Ν=3\) και \(Μ=4\).
Οπότε \(7=4^2-3^2\).

β) i) Έστω οι διαδοχικοί ακέραιοι \(k,\ k+1, k\in\mathbb{Z}\).
Η διαφορά των τετραγώνων τους είναι

\begin{align}(k+1)^2-k^2&=k^2+2k+1-k^2\\ &=2k+1,\ k\in\mathbb{Z},\end{align}

ο οποίος είναι περιττός αριθμός.

ii) Έχουμε ότι \(2021=2\cdot 1010+1\). Από την απόδειξη στο προηγούμενο ερώτημα έχουμε:

$$2021=(1010+1)^2-(1010)^2=1011^2-1010^2.$$

γ) Η γραμμοσκιασμένη περιοχή έχει εμβαδόν όσο η διαφορά των εμβαδών των τετραγώνων \(ΑΒΓΔ\) και \(ΓΗΡΚ\).
Το τετράγωνο \(ΑΒΓΔ\) έχει πλευρά \(ν+1\), ενώ το \(ΓΗΡΚ\) έχει πλευρά \(ν\).
Ισχύει \((ν+1)^2-ν^2=45\), οπότε

$$2ν+1=45\iff 2ν=44\iff ν=22.$$

Οι πλευρές \(x_1, x_2\) ενός ορθογωνίου παραλληλογράμμου είναι οι ρίζες της εξίσωσης

$$x^2-4\Big(λ+\frac{1}{λ}\Big)x+16=0$$

όπου \(λ > 0\).

α) Να βρείτε:
i. την περίμετρο \(Π\) του ορθογωνίου συναρτήσει του \(λ\).
(Μονάδες 6)
ii. το εμβαδόν \(Ε\) του ορθογωνίου.
(Μονάδες 6)

β) Να αποδείξετε ότι \(Π\geq 16\), για κάθε \(λ > 0\).
(Μονάδες 7)

γ) Για ποια τιμή του \(λ\) η περίμετρος \(Π\) του ορθογωνίου γίνεται ελάχιστη, δηλαδή ίση με \(16\); Τι μπορείτε να πείτε τότε για το ορθογώνιο;
(Μονάδες 6)

α) Από τους τύπους για το άθροισμα και το γινόμενο των ριζών εξίσωσης \(2^\text{ου}\) βαθμού έχουμε:

\begin{align}S&=x_1+x_2\\ &=-\frac{β}{α}\\ &=-\frac{-4(λ+\frac{1}{λ})}{1}\\ &=4\Big(λ+\frac{1}{λ}\Big)\end{align}

και

\begin{align}P&=x_1\cdot x_2\\ &=\frac{γ}{α}\\ &=\frac{16}{1}\\ &=1.\end{align}

Αφού \(P=x_1 \cdot x_2 =16 > 0\) και \(S =x_1 + x_2= 4\Big(λ+\frac{1}{λ}\Big)> 0\) για κάθε \(λ > 0\), οι ρίζες \(x_1, x_2\) είναι θετικές και άρα μπορούν να αποτελούν πλευρές ορθογωνίου.

i. Η περίμετρος του ορθογωνίου είναι:

\begin{align}Π&=2x_1+2x_2\\ &=2(x_1+x_2)\\ &=2\cdot 4\Big(λ+\frac{1}{λ}\Big)\\ &=8\Big(λ+\frac{1}{λ}\Big).\end{align}

ii. Το εμβαδόν είναι:

$$E=x_1\cdot x_2=16.$$

β) Έχουμε ισοδύναμα:

\begin{align}&Π\geq 16\\ \iff&8\left(λ+\frac{1}{λ}\right)\geq 16\\ \iff&λ+\frac{1}{λ}\geq 2\\ \iff&λ+\frac{1}{λ}-2\geq 0\\ \iff&\frac{λ^2-2λ+1}{λ}\geq 0\\ \iff&\frac{(λ-1)^2}{λ}\geq 0,\end{align}

που ισχύει για κάθε \(λ > 0\).
γ) Ισοδύναμα βρίσκουμε:

\begin{align}&Π=16\\ \iff&\frac{(λ-1)^2}{λ}=0\\ \iff&(λ-1)^2=0\\ \iff&λ=1.\end{align}

Για \(λ=1\) η περίμετρος είναι \(16\) (δηλαδή \(2(x_1+x_2)=16\) και τελικά \(x_1+x_2=8\)) και το εμβαδόν είναι \(16\) (δηλαδή \(x_1\cdot x_2=16\)), οπότε \(x_1=x_2=4\).
Επομένως, το ορθογώνιο είναι τετράγωνο.

Δίνεται η συνάρτηση

$$f(x)=3x^2+6αx+6β,\ α,β\in\mathbb{R}.$$

α) Να δείξετε ότι:

$$f(α)+f(β)\geq β^2-36.$$

(Μονάδες 8)

β) Να βρείτε τις τιμές των \(α, β\in\mathbb{R}\) για τις οποίες ισχύει

$$f(α)+f(β)=β^2-36.$$

(Μονάδες 6)

γ) Αν \(α=2\) και \(β=-6\):
i. Να λύσετε την εξίσωση \(f(x)=6x\).
(Μονάδες 6)
ii. Αν \(x_1,x_2\) οι ρίζες της εξίσωσης του ερωτήματος (γ.i), να δείξετε ότι ισχύει:

$$\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{6}.$$

(Μονάδες 5)

α) Έχουμε:

\begin{align}&f(α)+f(β)\geq α^2-36\\ \iff&3α^2+6α^2+6β+3β^2+6αβ+6β\geq β^2-36\\ \iff&9α^2+2β^2+6αβ+12β+36\geq 0\\ \iff&(9α^2+β^2+6αβ)+(β^2+12β+36)\geq 0\\ \iff&(3α+β)^2+(β+6)^2\geq 0,\end{align}

που ισχύει σαν άθροισμα τετραγώνων.
β) Βάσει του ερωτήματος (α), έχουμε:

\begin{align}&f(α)+f(β)\geq β^2-36\\ \iff&(3α+β)^2+(β+6)^2\geq 0\end{align}

για κάθε \(α, β\in\mathbb{R}\). Η ισότητα ισχύει αν και μόνον αν \(3α+β=0\) και \(β+6=0\).
Άρα \(β=-6\) και \(α=2\).
γ) Για \(α=2\) και \(β=-6\)
i. Λύνουμε την εξίσωση:

\begin{align}&f(x)=6x\\ \iff&3x^2+12x-36=6x\\ \iff&3x^2+12x-36-6x=0\\ \iff&3x^2+6𝑥-36=0\\ \iff&x^2+2x-12=0.\end{align}

Η διακρίνουσα του τριωνύμου \(x^2+2x-12\) είναι:

$$Δ=4+48=52=4\cdot 13$$

και οι ρίζες:

\begin{align}&x_{1,2}=\frac{-2\pm 2\sqrt{13}}{2}\\ \iff&x_1=-1+\sqrt{13}\text{ και }x_2=-1-\sqrt{13}.\end{align}

ii. Ισχύει ότι:

$$\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1\cdot x_2}=\frac{-2}{-12}=\frac{1}{6},$$

αφού \(x_1+x_2=-2\) και \(x_1\cdot x_2=-12\).
Εναλλακτικά:

\begin{align}\frac{1}{x_1}+\frac{1}{x_2}&=\frac{1}{-1+\sqrt{13}}+\frac{1}{-1-\sqrt{13}}\\ &=\frac{-1-\sqrt{13}-1+\sqrt{13}}{(-1-\sqrt{13})\cdot(-1+\sqrt{13})}\\ &=\frac{-2}{1-13}\\ &=\frac{-2}{-12}\\ &=\frac{1}{6}.\end{align}

α) Δίνεται η εξίσωση:

$$x^{4}-8x^{2}-9=0$$

Να δείξετε ότι η εξίσωση αυτή έχει δύο μόνο πραγματικές ρίζες, τις οποίες και να προσδιορίσετε.
(Μονάδες 10)

β) Γενικεύοντας το παράδειγμα του προηγούμενου ερωτήματος, θεωρούμε την εξίσωση: \(x^{4}+βx^{2}+γ=0\) \((1)\) με παραμέτρους \(β,γ\in \mathbb{R}\).
Να δείξετε ότι αν \(γ<0\), τότε:

1. \(β^{2}-4γ>0\)
   (Μονάδες 3)

2. Η εξίσωση \((1)\) έχει δύο μόνο διαφορετικές πραγματικές ρίζες.
   (Μονάδες 12)

ΛΥΣΗ

α) Θέτοντας στην εξίσωση \(x^{4}-8x-9=0\) όπου \(x^{2}=u\ge 0\), γίνεται:

$$u^{2}-8u-9=0$$

Το τριώνυμο έχει \(α=1\), \(β=-8\), \(γ=-9\) και διακρίνουσα:

$$Δ=β^{2}-4αγ=(-8)^{2}-4\cdot 1\cdot (-9)=64+39=100>0$$

Οι ρίζες του είναι οι:

$$u_{\text{1,2}}=\dfrac{-β\pm \sqrt{Δ}}{2α}$$ $$=\dfrac{-(-8)\pm \sqrt{100}}{2}$$ $$=\begin{cases} \dfrac{8+10}{2}=\dfrac{18}{2}=9>0\ \ \text{δεκτή} \\ \dfrac{8-10}{2}=\dfrac{-2}{2}=-1<0\ \ \text{απορρίπτεται} \end{cases}$$

Όμως έχουμε:

$$x^{2}=u $$ $$\Leftrightarrow x^{2}=9 $$ $$\Leftrightarrow x=\pm \sqrt{9} $$ $$\Leftrightarrow x=\pm 3$$

β) Όπως και στο ερώτημα α), η εξίσωση \(x^{4}-βx^{2}+γ=0\), αν θέσουμε όπου \(x^{2}=u\) με \(u\ge 0\), ισοδύναμα γίνεται:

$$u^{2}+βu+γ=0$$

1. Το τριώνυμο έχει διακρίνουσα \(Δ=β^{2}-4γ\), με \(β^{2}\ge 0\) και \(γ<0\) οπότε \(-γ>0\).
   Συνεπώς, \(Δ>0\) ως άθροισμα ενός μη αρνητικού και ενός θετικού αριθμού.

2. Επειδή \(Δ>0\) το τριώνυμο έχει δύο άνισες ρίζες \(u_{1},u_{2}\). Από τους τύπους Vietaτο γινόμενο των ριζών είναι \(Ρ=\dfrac{γ}{α}=γ<0\). Άρα, οι ρίζες είναι μη μηδενικές και ετερόσημες.
   Έστω:
   \(\begin{cases} u_{1}<0\ \text{,}\ &\text{απορρίπτεται} \\ u_{2}>0\ \text{,}\ &\text{δεκτή} \end{cases}\).
   Τότε έχουμε:

$$x^{2}=u_{2} $$ $$\Leftrightarrow x=\pm \sqrt{u_{2}}$$

α) Να λύσετε τις εξισώσεις

$$3x^{2}-14x+8=0\ \ \ \ (1)$$

και

$$8x^{2}-14x+3=0\ \ \ \ (2)$$

(Μονάδες10)

β) Ένας μαθητής παρατήρησε ότι οι ρίζες της εξίσωσης \((2)\) είναι οι αντίστροφες των ριζών της εξίσωσης \((1)\) και ισχυρίστηκε ότι το ίδιο θα ισχύει για οποιοδήποτε ζευγάρι εξισώσεων της μορφής:

$$αx^{2}+βx+γ=0\ \ \ \ (3)$$

και

$$γx^{2}+βx+α=0\ \ \ \ (4)$$

με

$$α\cdot γ\ne 0$$

Να αποδείξετε τον ισχυρισμό του μαθητή, δείχνοντας ότι:
Αν ο αριθμός \(ρ\) είναι ρίζα της εξίσωσης \((3)\) και \(α\cdot γ\ne 0\), τότε

1. \(ρ\ne 0\).
   (Μονάδες 5)

2. \(\dfrac{1}{ρ}\) είναι ρίζα της εξίσωσης \((4)\).
   (Μονάδες 10)

ΛΥΣΗ

α) Το τριώνυμο \(3x^{2}-14x+8\) έχει διακρίνουσα:

$$Δ=(-14)^{2}-4\cdot 3\cdot 8$$ $$=196-96=100>0$$

οπότε η εξίσωση \(3x^{2}-14x+8=0\) έχει δυο ρίζες άνισες, τις:

$$x_{1}=\dfrac{-(-14)+\sqrt{100}}{2\cdot 3}$$ $$=\dfrac{14+10}{6}=4$$

και

$$x_{2}=\dfrac{-(-14)-\sqrt{100}}{2\cdot 3}$$ $$=\dfrac{14-10}{6}=\dfrac{4}{6}=\dfrac{2}{3}$$

Το τριώνυμο \(8x^{2}-14x+3\) έχει διακρίνουσα:

$$Δ=(-14)^{2}-4\cdot 8\cdot 3$$ $$=196-96=100>0$$

οπότε η εξίσωση \(8x^{2}-14x+3=0\) έχει δυο ρίζες άνισες, τις:

$$x_{1}=\dfrac{-(-14)+\sqrt{100}}{2\cdot 8}$$ $$=\dfrac{14+10}{16}=\dfrac{24}{16}=\dfrac{3}{2}$$

και

$$x_{2}=\dfrac{-(-14)-\sqrt{100}}{2\cdot 8}$$ $$=\dfrac{14-10}{16}=\dfrac{4}{16}=\dfrac{1}{4}$$

β) Ο αριθμός \(ρ\) είναι ρίζα της εξίσωσης \((3)\) αν και μόνο αν την επαληθεύει, δηλαδή αν και μόνο αν ισχύει:

$$αρ^{2}+βρ+γ=0\ \ \ \ (5)$$

1. Εάν \(ρ=0\), τότε από την σχέση \((5)\) προκύπτει \(γ=0\), που είναι άτοπο, αφού \(α\cdot γ\ne 0\). Άρα \(ρ\ne 0\).

2. Ο \(\dfrac{1}{ρ}\) είναι ρίζα της εξίσωσης \((4)\) αν και μόνο αν

$$γ(\dfrac{1}{ρ})^{2}+β\cdot \dfrac{1}{ρ}+α=0$$ $$\overset{(\cdot ρ^{2})}{ \Longleftrightarrow }γ+βρ+αρ^{2}=0$$

που ισχύει λόγω της σχέσης \((5)\).

α) Να λύσετε την εξίσωση: \(2x^2 - x - 6=0\ \ \ \ (1)\).
(Μονάδες 09)

β) Να λύσετε την ανίσωση: \(|x-1|<2\ \ \ \ (2)\).
(Μονάδες 09)

γ) Να εξετάσετε αν υπάρχουν τιμές του \(x\) που ικανοποιούν ταυτόχρονα τις σχέσεις \((1)\) και \((2)\).
(Μονάδες 07)

α) Το τριώνυμο \(2x^{2}–x–6\) έχει \(α=2\), \(β=–1\), \(γ=–6\) και διακρίνουσα:

$$Δ=β^{2}–4αγ=(–1)^{2}–4\cdot 2\cdot (–6)=1+48=49>0$$

Οι ρίζες του τριωνύμου είναι οι:

$$x_{1,2}=\dfrac{-β\pm \sqrt{Δ}}{2α}$$ $$=\dfrac{-(-1)\pm \sqrt{49}}{2\cdot 2}$$ $$=\dfrac{1\pm 7}{4}$$ $$=\begin{cases} \dfrac{1+7}{4} =2 \\ \dfrac{1-7}{4} = - \dfrac{3}{2} \end{cases} $$

β) Είναι:

$$|x–1| < 2 $$ $$\Leftrightarrow –2 < x–1 < 2 $$ $$\Leftrightarrow –2+1 < x–1+1 < 2+1 $$ $$\Leftrightarrow –1 < x < 3 $$

γ) Η τιμή του \(x\) που ικανοποιεί ταυτόχρονα τις σχέσεις \((1)\) και \((2)\) είναι η \(x = 2\).

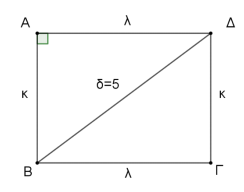
Δίνεται ορθογώνιο με διαστάσεις \(κ\) και \(λ\) του οποίου η περίμετρος είναι \(Π=14 \ cm\) και μια διαγώνιος \(δ=5 \ cm\).

α)

1. Με χρήση της ταυτότητας \((κ+λ)^{2}=κ^{2}+2κλ+λ^{2}\), να δείξετε ότι για το εμβαδόν \(Ε\) του ορθογωνίου ισχύει \(Ε=12 \ cm^{2}\).
   (Μονάδες 7)

2. Να αιτιολογήσετε γιατί οι διαστάσεις \(κ\) και \(λ\) του ορθογωνίου είναι ρίζες της εξίσωσης \(x^{2}-7x+12=0\).
   (Μονάδες 7)

3. Να βρείτε τις διαστάσεις \(κ\) και \(λ\) του ορθογωνίου.
   (Μονάδες 4)

β) Να δείξετε ότι ένα ορθογώνιο με περίμετρο \(Π=14 \ cm\) πρέπει να έχει εμβαδόν \(Ε\le \dfrac{49}{4}\).
(Μονάδες 7)

α)

1. Η περίμετρος του ορθογωνίου είναι \(Π=2κ+2λ\), οπότε:

$$2κ+2λ=14 $$ $$\Leftrightarrow κ+λ=7$$

Επίσης, εφαρμόζοντας το πυθαγόρειο θεώρημα στο τρίγωνο \(ΑΒΔ\) βρίσκουμε ότι

$$κ^{2}+λ^{2}=δ^{2} $$ $$\Leftrightarrow κ^{2}+λ^{2}=25$$

Από την ταυτότητα \((κ+λ)^{2}=κ^{2}+2κλ+λ^{2}\), έχουμε ότι:

$$7^{2}=25+2κλ $$ $$\Leftrightarrow 2κλ=49-25 $$ $$\Leftrightarrow κλ=12$$

Άρα, το εμβαδόν του ορθογωνίου είναι \(Ε=κλ=12\ cm\).

2. Δύο αριθμοί είναι ρίζες της εξίσωσης \(x^{2}-7x+12=0\) αν και μόνο αν έχουν άθροισμα \(S=-\dfrac{β}{α}=-\dfrac{(-7)}{1}=7\) και γινόμενο \(P=\dfrac{γ}{α}=\dfrac{12}{1}=12\). Από το ερώτημα αi) προκύπτει ότι οι διαστάσεις \(κ\) και \(λ\) ικανοποιούν τις συνθήκες αυτές, οπότε είναι ρίζες της εξίσωσης.

3. Το τριώνυμο \(x^{2}-7x+12\) έχει διακρίνουσα

$$Δ=(-7)^{2}-4\cdot 1\cdot 12$$ $$=49-48=1$$

και ρίζες

$$x_{\text{1,2}}=\dfrac{-(-7)\pm \sqrt{1}}{2\cdot 1}$$ $$=\begin{cases} \dfrac{7+1}{2}=4 \\ \dfrac{7-1}{2}=3 \end{cases}$$

Άρα, οι διαστάσεις του ορθογωνίου είναι \(3\ cm\) και \(4\ cm\).

β) Όπως και στο ερώτημα α), oι διαστάσεις ενός ορθογωνίου με περίμετρο \(Π=14\) και εμβαδόν \(Ε\) έχουν άθροισμα \(S=7\) και γινόμενο \(P=Ε\). Άρα, είναι ρίζες της εξίσωσης

$$x^{2}-7x+E=0$$

Η εξίσωση έχει λύσεις, δηλαδή υπάρχει τέτοιο ορθογώνιο, αν και μόνο αν για τη διακρίνουσα ισχύει

$$Δ\ge 0 $$ $$\Leftrightarrow (-7)^{2}-4\cdot 1\cdot Ε\ge 0 $$ $$\Leftrightarrow 49-4Ε\ge 0 $$ $$\Leftrightarrow Ε\le \dfrac{49}{4}$$

Έστω \(α\), \(β\) πραγματικοί αριθμοί για τους οποίους ισχύουν:

$$α\cdot β=4\ \ \text{και}\ \ α^{2}β+αβ^{2}=20$$

α) Να αποδείξετε ότι: \(α+β=5\).
(Μονάδες 10)

Β) Να κατασκευάσετε εξίσωση 2ου βαθμού με ρίζες τους αριθμούς \(α\), \(β\) και να τους βρείτε.
(Μονάδες 15)

α) Είναι:

$$α^{2}β+αβ^{2}=20 $$ $$\Leftrightarrow αβ(α+β)=20 $$ $$\Leftrightarrow 4(α+β)=20 $$ $$\Leftrightarrow α+β=5$$

β) Η ζητούμενη εξίσωση είναι της μορφής:

$$x^{2}-Sx+P=0$$

με:

$$S=α+β=5\ \ \text{και}\ \ P=α\cdot β=4$$

Τελικά η ζητούμενη εξίσωση είναι η:

$$x^{2}-5x+4=0$$

Το τριώνυμο \(x^{2}-5x+4\) έχει \(α=1\), \(β=-5\), \(γ=4\) και διακρίνουσα:

$$Δ=β^{2}-4αγ$$ $$=(-5)^{2}-4\cdot 1\cdot 4$$ $$=25-16=9>0$$

Οι ρίζες του τριωνύμου είναι οι:

$$x_{\text{1,2}}=\dfrac{-β\pm \sqrt{Δ}}{2α}$$ $$=\dfrac{-(-5)\pm \sqrt{9}}{2\cdot 1}$$ $$=\dfrac{5\pm 3}{2}$$ $$=\begin{cases} \dfrac{5+3}{2}=4 \\ \dfrac{5-3}{2}=1 \end{cases}$$