Μάθημα : Α΄ΛΥΚΕΙΟΥ - ΑΛΓΕΒΡΑ

Μια δεξαμενή έχει σχήμα ορθογωνίου παραλληλεπιπέδου με βάση τετράγωνο και ύψος ίσο με το ένα τέταρτο του μήκους της.

α) Αν η δεξαμενή έχει όγκο \(16\ m^3\), να βρείτε τις διαστάσεις της.
(Μονάδες 8)

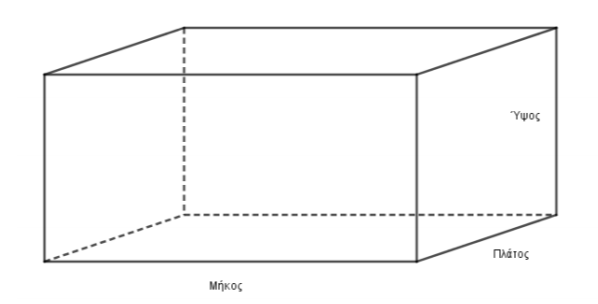
β) Λόγω έλλειψης χώρου η δεξαμενή ανακατασκευάζεται με βάση ορθογώνιο παραλληλόγραμμο και ύψος \(2\) μέτρα (όπως στο παρακάτω σχήμα). Αν το πλάτος της νέας δεξαμενής είναι κατά \(2\ m\) μικρότερο από το μήκος της υπολογίστε τις διαστάσεις της βάσης προκειμένου ο όγκος να παραμείνει \(16\ m^3\).
(Μονάδες 9)

γ) Αν η νέα δεξαμενή περιέχει \(10\ m^3\) πετρέλαιο να βρείτε το ύψος της στάθμης του πετρελαίου μέσα στη δεξαμενή.
(Μονάδες 8)

α) Γνωρίζουμε ότι ο όγκος της δεξαμενής ισούται με το γινόμενο των τριών διαστάσεων της. Επειδή η δεξαμενή έχει βάση τετράγωνη θέτουμε \(x\) το μήκος και το πλάτος της οπότε το ύψος της θα είναι \(\frac{x}{4}\). Άρα ο όγκος της δεξαμενής \(V\) θα είναι:

$$V=x\cdot x\cdot \frac{x}{4}=\frac{x^3}{4}$$

Αφού η δεξαμενή έχει όγκο \(V=16m^3\) θα έχουμε:

\begin{align}&V=16\\ \iff&\frac{x^3}{4}=16\\ \iff&x^3=64\\ \iff&x=\sqrt[3]{64}\\ \iff&x=\sqrt[3]{4^3}\\ \iff&x=4m.\end{align}

Οπότε η δεξαμενή έχει μήκος και πλάτος ίσα με \(4m\) και ύψος ίσο με \(1m\).

β) Έστω \(x,\ (x>0)\) το μήκος της δεξαμενής. Τότε το πλάτος της θα είναι \(x-2\) και ο όγκος της δεξαμενής θα ισούται με \(V=2x(x-2)\).
Οπότε έχουμε:

\begin{align}&V=16\\ \iff&2x(x-2)=16\\ \iff&x(x-2)=8\\ \iff&x^2-2𝑥=8\\ \iff&x^2-2𝑥-8=0\end{align}

Έχουμε

\begin{align}Δ=&β^2-4\cdot α\cdot γ\\ =&(-2)^2-4\cdot 1\cdot (-8)\\ =&4+32\\ =&36>0.\end{align}

Τότε:

\begin{align}&x_{1,2}=\frac{-β\pm\sqrt{Δ}}{2\cdot α}\\ \iff&x_{1,2}=\frac{2\pm\sqrt{36}}{2\cdot1}\\ \iff&x_{1,2}=\frac{2\pm6}{2}\\ \iff&x_{1,2}=\begin{cases}\frac{2-6}{2}\\ \frac{2+6}{2}\end{cases}\\ \iff&x_{1,2}=\begin{cases}-2,\text{ απορρίπτεται γιατί πρέπει } x>0\\ 4,\text{ δεκτή }\end{cases}\end{align}

Άρα το μήκος της δεξαμενής είναι \(4m\) και το πλάτος \(2m\).

γ) Αφού η νέα δεξαμενή περιέχει \(10m^3\) πετρέλαιο και η βάση της έχει μήκος \(4m\) και πλάτος \(2m\), αν \(x\) είναι το ύψος του υγρού μέσα στη δεξαμενή ο όγκος του υγρού θα είναι:

\begin{align}&V_{πετρ.}=10\\ \iff&4\cdot 2\cdot x=10\\ \iff&8\cdot x=10\\ \iff&x=\frac{10}{8}\\ \iff&x=\frac{5}{4}m.\end{align}

Άρα το ύψος του υγρού στη δεξαμενή είναι \(\frac{5}{4}m\).

α) Να αποδείξετε ότι οι παρακάτω ανισότητες ισχύουν για κάθε \(x\in\mathbb{R}\) και να βρειτε για ποιες τιμές του \(x\) ισχύουν ως ισότητες.
i. \(x^2+x+1\geq\dfrac{3}{4}\).
(Μονάδες 4)
ii. \(x^2-x+1\geq\dfrac{3}{4}\).
(Μονάδες 4)

β) Να δείξετε ότι

$$(x^2+x+1)(x^2-x+1) > \frac{9}{16}$$

για κάθε \(x\in\mathbb{R}\).
(Μονάδες 6)

γ) Δίνεται η παράσταση \(A=\dfrac{(x^3-1)(x^3+1)}{x^2-1}\).

i. Να βρείτε για ποιες τιμές του \(x\in\mathbb{R}\) ορίζεται η παράσταση \(A\).
(Μονάδες 5)
ii. Με τη βοήθεια του (β) ή με οποιοδήποτε άλλο τρόπο θέλετε, να εξετάσετε αν η παράσταση \(A\) μπορεί να πάρει την τιμή \(\dfrac{9}{16}\).
(Μονάδες 6)

ΛΥΣΗ
α) Ισοδύναμα έχουμε
i.

\begin{align}&x^2+x+1\geq\frac{3}{4}\\ \iff&x^2+x+1-\frac{3}{4}\geq 0\\ \iff&x^2+x+\frac{1}{4}\geq 0\\ \iff&\left(x+\frac{1}{2}\right)^2\geq 0,\end{align}

που ισχύει.
Ως ισότητα ισχύει αν και μόνο αν

$$x+\frac{1}{2}=0\iff x=-\frac{1}{2}.$$

ii.

\begin{align}&x^2-x+1\geq\frac{3}{4}\\ \iff&x^2-x+1-\frac{3}{4}\geq 0\\ \iff&x^2-x+\frac{1}{4}\geq 0\\ \iff&\left(x-\frac{1}{2}\right)^2\geq 0,\end{align}

που ισχύει.
Ως ισότητα ισχύει αν και μόνο αν

$$x-\frac{1}{2}=0\iff x=\frac{1}{2}.$$

β) Για \(x\neq\dfrac{1}{2}\) και \(x\neq-\dfrac{1}{2}\), όπως δείξαμε στο (α) ερώτημα, είναι \(x^2+x+1 > \dfrac{3}{4}\) και \(x^2-x+1 > \dfrac{3}{4}\), οπότε με πολλαπλασιασμό κατά μέλη έχουμε

$$(x^2+x+1)(x^2-x+1) > \frac{9}{16}.$$

Επίσης, για \(x=\dfrac{1}{2}\) είναι \(x^2+x+1 > \dfrac{3}{4}\) και \(x^2-x+1=\dfrac{3}{4}\), οπότε με πολλαπλασιασμό κατά μέλη έχουμε

$$(x^2+x+1)(x^2-x+1) > \frac{9}{16}.$$

Τέλος, για \(x=-\dfrac{1}{2}\) είναι \(x^2+x+1=\dfrac{3}{4}\) και \(x^2-x+1 > \dfrac{3}{4}\), οπότε με πολλαπλασιασμό κατά μέλη έχουμε

$$(x^2+x+1)(x^2-x+1) > \frac{9}{16}.$$

Επομένως

$$(x^2+x+1)(x^2-x+1) > \frac{9}{16}.$$

για κάθε \(x\in\mathbb{R}\).
γ) i. Η παράσταση \(A\) ορίζεται για κάθε πραγματική τιμή του \(x\) για την οποία ισχύει

$$x^2\neq 1\iff x\neq \pm1.$$

ii. Είναι

\begin{align}A&=\frac{(x^3-1)(x^3+1)}{x^2-1}\\ &=\frac{(x-1)(x^2+x+1)(x+1)(x^2-x+1)}{(x-1)(x+1)}\\ &=(x^2+x+1)(x^2-x+1)\end{align}

για κάθε \(x\in\mathbb{R}-\{1,-1\}\).
Όπως δείξαμε στο (β) είναι

$$(x^2+x+1)(x^2-x+1) > \frac{9}{16}$$

για κάθε \(x\in\mathbb{R}\), οπότε \(A > \dfrac{9}{16}\) για κάθε \(x\in\mathbb{R}-\{1,-1\}\) και επομένως η παράσταση \(A\) δεν μπορεί να πάρει την τιμή \(\dfrac{9}{16}\).
Εναλλακτικά, θα εξετάσουμε αν η εξίσωση

$$\frac{(x^3-1)(x^3+1)}{x^2-1}=\frac{9}{16}$$

έχει λύση στο \(\mathbb{R}-\{1,-1\}\). Είναι ισοδύναμα

\begin{align}&\frac{(x^3-1)(x^3+1)}{x^2-1}=\frac{9}{16}\\ \iff&\frac{x^6-1}{x^2-1}=\frac{9}{16}\\ \iff&\frac{(x^2)^3-1}{x^2-1}=\frac{9}{16}\\ \iff&\frac{(x^2-1)(x^4+x^2+1)}{x^2-1}=\frac{9}{16}\\ \iff&16(x^4+x^2+1)=9\\ \iff&16x^4+16x^2+16-9=0\\ \iff&16x^4+16x^2+7=0,\end{align}

και επειδή

$$16x^4+16x^2+7\geq 7 > 0,$$

η εξίσωση είναι αδύνατη και επομένως η παράσταση \(A\) δεν μπορεί να πάρει την τιμή \(\dfrac{9}{16}\).