Μάθημα : Β΄ΛΥΚΕΙΟΥ - ΜΑΘΗΜΑΤΙΚΑ ΠΡ. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
Κωδικός : G217111
G217111 - ΧΡΗΣΤΟΣ ΤΡΙΑΝΤΗΣ
Ενότητες μαθήματος - Κεφάλαιο 2ο: Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ - Λυμένα θέματα από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
Κεφάλαιο 2ο: Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ - Λυμένα θέματα από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
2.1 ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ
Θέμα: 14970
ΘΕΜΑ 4
Δίνεται η ευθεία \(y=λ(x-2)+λ-2\), \(λ\in \mathbb{R}\ \ \ \ (1)\).
α) Να βρείτε τις ευθείες που προκύπτουν όταν \(λ=1\) και όταν \(λ=2\). Κατόπιν να βρείτε το κοινό σημείο \(Μ\) των δυο ευθειών.
(Μονάδες 7)
Έστω \(Μ(1,-2)\).
β) Να αποδείξετε ότι όλες οι ευθείες που προκύπτουν από την \((1)\) για τις διάφορες τιμές του \(λ\), διέρχονται από το \(Μ\).
(Μονάδες 5)
γ) Να βρείτε:
-
τα σημεία τομής \(Α\), \(Β\) της ευθείας \((1)\) με τους άξονες \(x'x\) και \(y'y\).
(Μονάδες 6) -
για ποιες τιμές του \(λ\) το εμβαδόν του τριγώνου \(ΟΑΒ\) είναι ίσο με \(\dfrac{1}{2}\).
(Μονάδες 7)
Απάντηση Θέματος: 14970
ΛΥΣΗ
α) Με \(λ=1\) έχουμε:
$$y=x-2+1-2 $$ $$\Rightarrow y=x-3$$
ενώ με \(λ=2\) έχουμε:
$$y=2x-4$$
Οι συντεταγμένες του \(Μ\) προκύπτουν από τη λύση του αντίστοιχου συστήματος. Είναι:
$$\begin{cases} y=x-3 \\ y=2x-4 \end{cases} $$ $$\Leftrightarrow \begin{cases} y=x-3 \\ x-3=2x-4 \end{cases} $$ $$\Leftrightarrow \begin{cases} x=1 \\ y=x-3 \end{cases} $$ $$\Leftrightarrow \begin{cases} x=1 \\ y=-2 \end{cases}$$
Επομένως το κοινό σημείο των δυο ευθειών είναι το \(Μ(1,-2)\).
β) Αρκεί να αποδείξουμε ότι οι συντεταγμένες του \(Μ\) επαληθεύουν την εξίσωση της ευθείας. Με \(x=1\) η εξίσωση γράφεται:
$$y=λ(1-2)+λ-2 $$ $$\Leftrightarrow y=-λ+λ-2 $$ $$\Leftrightarrow y=-2$$
οπότε πραγματικά κάθε ευθεία που προκύπτει από την δοσμένη εξίσωση διέρχεται από το \(Μ\).
γ)
- Με \(y=0\) στην δοσμένη εξίσωση παίρνουμε:
$$λ(x-2)+λ-2=0 $$ $$\Leftrightarrow λx-λ-2=0 $$ $$\Leftrightarrow λx=λ+2 $$ $$\Leftrightarrow x=\dfrac{λ+2}{λ}$$
Προφανώς \(λ\ne 0\), αφού με \(λ=0\) η εξίσωση είναι αδύνατη.
Με \(x=0\) στη δοσμένη εξίσωση παίρνουμε:
$$y=-2λ+λ-2 $$ $$\Leftrightarrow y=-λ-2$$
Επομένως η ευθεία τέμνει τον άξονα \(y'y\) στο σημείο \(A(0,-λ-2)\) και τον \(x'x\) στο σημείο \(B\left(\dfrac{λ+2}{λ},0\right)\).
- Ισχύει:
$$(ΟΑ)=|-λ-2|=|λ+2|$$
$$(ΟΒ)=\left|\dfrac{λ+2}{λ}\right|=\dfrac{|λ+2|}{|λ|}$$
και το εμβαδόν του τριγώνου \(ΟΑΒ\) είναι:
$$(ΟΑΒ)=\dfrac{1}{2}(ΟΑ)(ΟΒ)$$ $$=\dfrac{1}{2}\dfrac{|λ+2|^{2}}{|λ|}$$
Έτσι, έχουμε:
$$(ΟΑΒ)=\dfrac{1}{2} $$ $$\Leftrightarrow \dfrac{1}{2}\dfrac{|λ+2|^{2}}{|λ|}=\dfrac{1}{2} $$ $$\Leftrightarrow (λ+2)^{2}=|λ|$$
- Αν \(λ>0\), τότε έχουμε:
$$λ^{2}+4λ+4=λ $$ $$\Leftrightarrow λ^{2}+3λ+4=0$$
που δεν έχει πραγματικές ρίζες.
- Αν \(λ<0\), τότε έχουμε:
$$λ^{2}+4λ+4=-λ $$ $$\Leftrightarrow λ^{2}+5λ+4=0 $$ $$\Leftrightarrow λ=-1\ \ \text{ή}\ \ λ=-4$$
Θέμα: 15027
ΘΕΜΑ 2
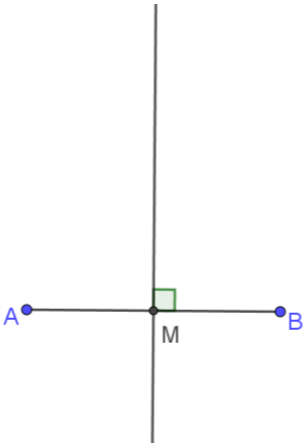
Δίνονται τα σημεία \(Α(1,-1)\) και \(Β(3,5)\) όπως φαίνεται στο παρακάτω σχήμα.
α) Να βρείτε το συντελεστή διεύθυνσης της ευθείας \(ΑΒ\).
(Μονάδες 7)
β) Να βρείτε τις συντεταγμένες του μέσου \(Μ\) του τμήματος \(ΑΒ\).
(Μονάδες 8)
γ) Να βρείτε την εξίσωση της μεσοκαθέτου του τμήματος \(ΑΒ\).
(Μονάδες 10)
Απάντηση Θέματος: 15027
α) Ο συντελεστής διεύθυνσης της ευθείας \(ΑΒ\) είναι
$$λ=\frac{5-(-1)}{3-1}=\frac{6}{2}=3.$$
β) Το μέσο \(Μ\) του \(ΑΒ\) έχει συντεταγμένες \(Μ\left(\dfrac{1+3}{2},\dfrac{-1+5}{2}\right)\), δηλαδή \(Μ(2,2)\).
γ) Αν \((ε)\) η ζητούμενη μεσοκάθετος, τότε
\begin{align}&(ε)\perp ΑΒ\\ \iff&λ_ε\cdot λ_{ΑΒ}=-1\\ \iff&λ_ε\cdot 3=-1\\ \iff&λ_ε=-\frac{1}{3}.\end{align}
Η ευθεία \((ε)\) διέρχεται από το σημείο \(Μ(2,2)\) και έχει συντελεστή διεύθυνσης \(λ_ε=-\dfrac{1}{3}\), οπότε
$$ε:y-2=-\frac{1}{3}(x-2).$$
Θέμα: 15029
ΘΕΜΑ 4
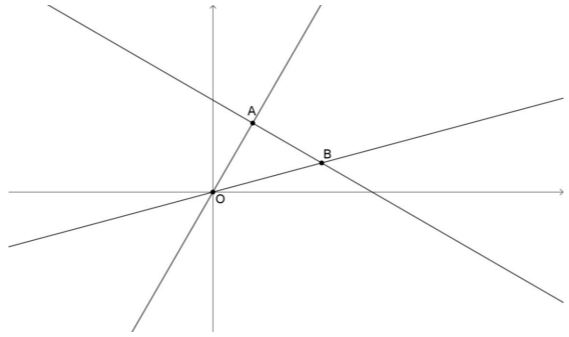
Στο παρακάτω σχήμα δίνονται τα σημεία \(Ο(0,0),\ Α(1,\sqrt{3}),\ Β(\sqrt{3}+1,\sqrt{3}-1)\).
α) Να βρείτε την εξίσωση της ευθείας \(ΟΑ\) καθώς και τη γωνία \(ω\) που σχηματίζει με τον άξονα \(x'x\).
(Μονάδες 6)
β) Να βρείτε την εξίσωση της ευθείας \(ΑΒ\) καθώς και τη γωνία \(φ\) που σχηματίζει με τον άξονα \(x'x\).
(Μονάδες 6)
γ) Να δείξετε ότι το τρίγωνο \(ΟΑΒ\) είναι ορθογώνιο και ισοσκελές με \(\hat{Α}=90^\circ\).
(Μονάδες 7)
δ) Να δείξετε ότι \(εφ15^\circ=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\).
(Μονάδες 6)
Απάντηση Θέματος: 15029
α) Η κλίση της ευθείας \(ΟΑ\) είναι
$$λ_{ΟΑ}=\frac{\sqrt{3}-0}{1-0}=\sqrt{3}$$
και επειδή διέρχεται από την αρχή των αξόνων θα έχει εξίσωση \(y=\sqrt{3}\cdot x\). Η γωνία \(ω\) που σχηματίζει με τον \(x'x\) έχει εφαπτομένη \(\sqrt{3}\), οπότε είναι \(ω=60^\circ\).
β) Η κλίση της ευθείας \(ΑΒ\) είναι
$$λ_{ΑΒ}=\frac{\sqrt{3}-1-\sqrt{3}}{\sqrt{3}+1-1}=\frac{-1}{\sqrt{3}}=-\frac{\sqrt{3}}{3}$$
και αφού διέρχεται από το σημείο \(Α(1,\sqrt{3})\) έχει εξίσωση
\begin{align}&y-\sqrt{3}=-\frac{\sqrt{3}}{3}(x-1)\\ \iff&y=-\frac{\sqrt{3}}{3}\cdot x+\frac{4\sqrt{3}}{3}.\end{align}
Η γωνία \(φ\) που σχηματίζει με τον \(x'x\) έχει εφαπτομένη \(-\dfrac{\sqrt{3}}{3}\), οπότε είναι \(φ=150^\circ\).
γ) Είναι
$$λ_{ΟΑ}\cdot λ_{ΑΒ}=\sqrt{3}\cdot\left(-\frac{\sqrt{3}}{3}\right)=-1,$$
δηλαδή \(ΟΑ\perp ΑΒ\), οπότε το τρίγωνο \(ΟΑΒ\) είναι ορθογώνιο με \(\hat{Α}=90^\circ\). Επίσης
\begin{align}(ΟΑ)&=\sqrt{(1-0)^2+(\sqrt{3}-0)^2}=2\\ (ΑΒ)&=\sqrt{(\sqrt{3}+1-1)^2+(\sqrt{3}-1-\sqrt{3})^2}=2\end{align}
και αφού \((ΟΑ)=(ΑΒ)\) το \(ΟΑΒ\) είναι και ισοσκελές.
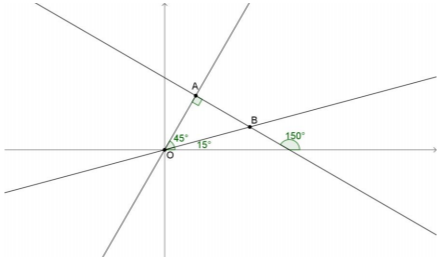
δ) Αν \(θ\) είναι η γωνία που σχηματίζει η ευθεία \(ΟΒ\) με τον \(x'x\), είναι
$$θ=ω-Α\hat{Ο}Β=60^\circ-45^\circ=15^\circ,$$
αφού \(Α\hat{Ο}Β=45^\circ\) δεδομένου ότι το τρίγωνο \(ΟΑΒ\) είναι ορθογώνιο και ισοσκελές με \(\hat{Α}=90^\circ\). Όμως \(εφθ=εφ15^\circ\) είναι η κλίση της ευθείας \(ΟΒ\), δηλαδή \(\dfrac{\sqrt{3}-1-0}{\sqrt{3}+1-0}=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\). Συνεπώς \(εφ15^\circ=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\).
Θέμα: 15044
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(0,5)\) και \(Β(6,-1)\).
α) i. Να βρείτε τον συντελεστή διεύθυνσης της ευθείας που διέρχεται από τα σημεία \(Α\) και \(Β\).
(Μονάδες 5)
ii. Να αποδείξετε ότι το μέσο του ευθύγραμμου τμήματος \(AB\) είναι το σημείο \(M(3,2)\).
(Μονάδες 5)
β) Να βρείτε την εξίσωση της μεσοκάθετης ευθείας \((ε)\) του ευθύγραμμου τμήματος \(ΑΒ\).
(Μονάδες 15)
Απάντηση Θέματος: 15044
α) i. Είναι
$$λ_{ΑΒ}=\frac{-1-5}{6-0}=-1.$$
ii. Aν \(M(x_M,y_M)\), ισχύει:
$$\begin{cases}x_M=\dfrac{x_A+x_B}{2}=3\\y_M=\dfrac{y_A+y_B}{2}=2\end{cases}$$
β) Η μεσοκάθετη ευθεία \((ε)\) του ευθύγραμμου τμήματος \(ΑΒ\) διέρχεται από το σημείο \(Μ(3,2)\) και έχει κλίση \(λ\), η οποία προκύπτει από την εξίσωση
$$λ\cdot λ_{ΑΒ}=-1$$ $$\iff λ\cdot(-1)=-1\iff λ=1.$$
Επομένως η εξίσωσή της είναι η
$$y-2=1\cdot(x-3)\iff y=x-1.$$
Θέμα: 15271
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(-3,2),\ Β(1,6)\) και \(Γ(-13,-7).\)
α) Να βρείτε το συντελεστή διεύθυνσης της ευθείας που διέρχεται από τα \(Α,\ Β.\)
(Μονάδες 8)
β) Να αποδείξετε ότι η ευθεία που διέρχεται από τα \(Α,\ Β\) έχει εξίσωση \(y=x+5.\)
(Μονάδες 7)
γ) Να αιτιολογήσετε γιατί το σημείο \(Γ\) δεν είναι πάνω στην \(ΑΒ.\)
(Μονάδες 10)
Απάντηση Θέματος: 15271
α) Η ευθεία που διέρχεται από τα σημεία \(Α,\ Β\) έχει συντελεστή διεύθυνσης
$$λ=\frac{6-2}{1+3}=1$$
β) Η ευθεία έχει συντελεστή διεύθυνσης \(λ=1\) και διέρχεται από το σημείο \(Α\), οπότε έχει εξίσωση \(y-2=1\cdot (x+3)\) δηλαδή είναι η \(y=x+5.\)
γ) Το σημείο \(Γ\) είναι πάνω στην ευθεία \(ΑΒ\) μόνο όταν οι συντεταγμένες του επαληθεύουν την εξίσωση της ευθείας \(ΑΒ.\)
Με \(x=-13\) στον τύπο της ευθείας \(ΑΒ\) έχουμε:
$$y=-13+5=-8\neq -7=y_Γ$$
Άρα το σημείο \(Γ\) δεν είναι πάνω στην \(ΑΒ.\)
Θέμα: 15275
ΘΕΜΑ 4
Σε ορθοκανονικό σύστημα συντεταγμένων θεωρούμε το σημείο \(Μ(2,1)\).
α) Μια ευθεία \((ε)\) με συντελεστή \(λ\) διέρχεται από το \(Μ\). Να βρείτε:
i. Την εξίσωση της.
(Μονάδες 2)
ii. Για ποιες τιμές του \(λ\) η ευθεία σχηματίζει τρίγωνο με τους άξονες.
(Μονάδες 5)
β) Έστω ότι η ευθεία \((ε)\) τέμνει τους άξονες \(x'x\) και \(y'y\) στα σημεία \(Α,Β\).
i. Να βρείτε, με τη βοήθεια του \(λ\), τα μήκη των τμημάτων \(ΟΑ, ΟΒ\).
(Μονάδες 6)
ii. Να βρείτε για ποιες τιμές του \(λ\) η ευθεία σχηματίζει με τους άξονες ισοσκελές τρίγωνο.
(Μονάδες 6)
iii. Να υπολογίσετε, σε κάθε περίπτωση, το εμβαδό του ισοσκελούς τριγώνου που σχηματίζεται.
(Μονάδες 6)
Απάντηση Θέματος: 15275
α) i. Αφού η ευθεία διέρχεται από το \(Μ\) και έχει συντελεστή διεύθυνσης \(λ\), η εξίσωση της είναι \(y-1=λ(x-2)\) που γράφεται \(y=λx-2λ+1\).
ii. Σε κάθε περίπτωση που ισχύει \(λ\neq0\) η ευθεία τέμνει και τους δυο άξονες και όταν δεν διέρχεται από την αρχή \(Ο\), δηλαδή όταν \(λ\neq\dfrac{1}{2}\), σχηματίζει τρίγωνο. Επομένως, η ευθεία σχηματίζει τρίγωνο με τους άξονες μόνο όταν \(λ\in\mathbb{R}-\left\{0,\dfrac{1}{2}\right\}\).
β) i. Με \(y=0\) στην εξίσωση της ευθείας, παίρνουμε \(x=\dfrac{2λ-1}{λ}\), οπότε \(Α\left(\dfrac{2λ-1}{λ},0\right)\), ενώ με \(x=0\) παίρνουμε \(y=-2λ+1\), οπότε \(Β(0,-2λ+1)\). Επομένως τα μήκη των τμημάτων \(ΟΑ, ΟΒ\) είναι \((ΟΑ)=\dfrac{|2λ-1|}{|λ|}\) και \((ΟΒ)=|-2λ+1|=|2λ-1|\).
ii. Η ευθεία σχηματίζει με τους άξονες ισοσκελές τρίγωνο, μόνο όταν \((ΟΑ)=(ΟΒ)\). Είναι:
\begin{align}&(ΟΑ)=(ΟΒ)\\ \iff&\frac{|2λ-1|}{|λ|}=|2λ-1|\\ \iff&|2λ-1|(|λ|-1)=0\\ \iff&|λ|-1=0\end{align}
αφού \(λ=\dfrac{1}{2}\). Άρα η ευθεία σχηματίζει ισοσκελές τρίγωνο όταν \(λ=-1\) ή \(λ=1\).
iii. Αν \(λ=-1\), τότε \((ΟΑ)=3\) και \((ΟΒ)=3\), οπότε το εμβαδόν \((ΟΑΒ)\) του τριγώνου \(ΟΑΒ\) είναι \((ΟΑΒ)=\dfrac{9}{2}\).
Αν \(λ=1\), τότε \((ΟΑ)=1\) και \((ΟΒ)=1\), οπότε το εμβαδόν του τριγώνου \(ΟΑΒ\) είναι \((ΟΑΒ)=\dfrac{1}{2}\).
Σχόλιο:
Το τρίγωνο \(ΟΑΒ\) είναι ορθογώνιο και ισοσκελές, οπότε η γωνία που σχηματίζει η ευθεία (υποτείνουσα) με τον άξονα \(x'x\) είναι \(45^\circ\) ή \(135^\circ\). Έτσι, έχουμε \(λ=εφ45^\circ=1\) ή \(λ=εφ135^\circ\) που είναι οι τιμές που βρήκαμε παραπάνω.
Θέμα: 15657
ΘΕΜΑ 2
Δίνονται οι ευθείες: \(ε_1:\ 2x+y=6\) και \(ε_2:\ x-2y=-2\)
α) Να βρείτε το κοινό τους σημείο \(M.\)
(Μονάδες 12)
β) Να δείξετε ότι οι ευθείες \((ε_1), (ε_2)\) και \((ε_3):\ 3x-y=4\) διέρχονται από το ίδιο σημείο.
(Μονάδες 13)
Απάντηση Θέματος: 15657
α) Για να βρούμε το κοινό σημείο των ευθειών \((ε_1)\) και \((ε_2)\) θα λύσουμε το σύστημα:
$$\begin{align} & \begin{cases} 2x+y=6 \\ x-2y=-2\end{cases} \\ \Leftrightarrow & \begin{cases} 2x+y=6 \\ 2x-4y=-4\end{cases} \\ \Leftrightarrow & \begin{cases} 5y=10 \\ x-2y=-2\end{cases} \\ \Leftrightarrow & \begin{cases} y=2 \\ x=2\end{cases}\end{align}$$
Οπότε το σημείο \(Μ\) έχει συντεταγμένες \(Μ(2,2).\)
β) Οι ευθείες \((ε_1)\) και \((ε_2)\) και \((ε_3):\ 3x-y=4\) θα διέρχονται από το ίδιο σημείο, εάν η ευθεία \(3x-y=4\) διέρχεται από το \(M(2,2)\), δηλαδή εάν: \(3\cdot 2-2=4\), που ισχύει.
Θέμα: 16002
ΘΕΜΑ 2
Σε τρίγωνο \(ΑΒΓ\) είναι \(Α(3,-2)\) και \(Γ(5,2)\). Αν το σημείο \(Μ\left(3,\dfrac{1}{2}\right)\) είναι το μέσο της \(ΒΓ\), τότε:
α) Να αποδείξετε ότι \(Β(1,-1)\).
(Μονάδες 9)
β) Να βρείτε το μήκος της πλευράς \(ΒΓ\).
(Μονάδες 6)
γ) Να βρείτε την εξίσωση της ευθείας \(ΑΓ\).
(Μονάδες 10)
Απάντηση Θέματος: 16002
α) Αν \(Β(x,y)\), τότε έχουμε \(\dfrac{x+5}{2}=3\) και \(\dfrac{y+2}{2}=\dfrac{1}{2}\), οπότε \(x=1\) και \(y=-1\), άρα \(Β(1,-1)\).
β) Το μήκος της πλευράς \(ΒΓ\) είναι
\begin{align}(BΓ)&=\sqrt{(5-1)^2+(2+1)^2}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ &=5.\end{align}
γ) Η ευθεία \(ΑΓ\) διέρχεται από το σημείο \(Α(3,-2)\) και έχει συντελεστή διεύθυνσης
$$λ=\frac{2+2}{5-3}=\frac{4}{2}=2,$$
οπότε η εξίσωσή της είναι η \(y+2=2(x-3)\), που γράφεται \(y=2x-8\).
Θέμα: 16766
ΘΕΜΑ 2
Δίνονται οι ευθείες \((ε_1)\) και \((ε_2)\) με εξισώσεις \(x-3y=4\) και \(9x+3y=6\) αντίστοιχα.
α) Να αποδείξετε ότι οι ευθείες \((ε_1)\) και \((ε_2)\) είναι κάθετες.
(Μονάδες 8)
β) Να αποδείξετε ότι οι ευθείες \((ε_1)\) και \((ε_2)\) τέμνονται στο σημείο \(Α(1,-1)\).
(Μονάδες 8)
γ) Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σημείο \(Α\) και είναι κάθετη στον άξονα \(x'x\).
(Μονάδες 9)
Απάντηση Θέματος: 16766
α) Η ευθεία \((ε_1)\) έχει εξίσωση \(x-3y-4=0\) και συντελεστή διεύθυνσης
$$λ_1=-\frac{Α}{Β}=-\frac{1}{-3}=\frac{1}{3}.$$
Η ευθεία \((ε_2)\) έχει εξίσωση \(9x+3y-6=0\) και συντελεστή διεύθυνσης
$$λ_2=-\frac{Α}{Β}=-\frac{9}{3}=-3.$$
Παρατηρούμε ότι \(λ_1λ_2=\dfrac{1}{3}(-3)=-1\). Άρα, οι ευθείες \((ε_1)\) και \((ε_2)\) είναι κάθετες.
β) Προσθέτουμε τις δύο εξισώσεις κατά μέλη, οπότε
$$10x=10\iff x=1.$$
Αντικαθιστούμε στην εξίσωση \(9x+3y=6\) και έχουμε διαδοχικά
\begin{align}&9+3y=6\\ \iff&3y=-3\\ \iff&y=-1.\end{align}
Άρα, το σημείο τομής των ευθειών \((ε_1)\) και \((ε_2)\) είναι το \(Α(1,-1)\).
γ) Γνωρίζουμε ότι η ευθεία που διέρχεται από το σημείο \(Α(x_0,y_0)\) και είναι κάθετη στον άξονα \(x'x\) έχει εξίσωση \(x=x_0\). Επομένως, η εξίσωση της ζητούμενης ευθείας είναι \(x=1\).
Θέμα: 17078
ΘΕΜΑ 4
Δίνονται τα σημεία \(A(3,2α)\), \(Β(4,α)\), \(Γ(α+1,1-α)\) και \(Δ(α,1)\), με \(α\in\mathbb{R}\).
α) Να αποδείξετε ότι:
i. Η ευθεία που διέρχεται από τα σημεία \(A\) και \(B\) έχει εξίσωση \(y=-αx+5α\).
(Μονάδες 6)
ii. Τα σημεία \(Γ\) και \(Δ\) ανήκουν στην ευθεία \(ΑΒ\) αν και μόνο αν \(α=\dfrac{5\pm\sqrt{21}}{2}\).
(Μονάδες 7)
iii. Το τετράπλευρο \(ABΓΔ\) είναι παραλληλόγραμμο όταν \(α\neq\dfrac{5\pm\sqrt{21}}{2}\).
(Μονάδες 7)
β) Θεωρήστε τον ισχυρισμό:
Υπάρχει πραγματικός αριθμός \(α\) ώστε το τετράπλευρο \(ΑΒΓΔ\) να είναι τετράγωνο.
Είναι αληθής ή ψευδής ο παραπάνω ισχυρισμός; Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 5)
Απάντηση Θέματος: 17078
α) i) Ο συντελεστής διεύθυνσης \(λ\) της ευθείας που διέρχεται από τα σημεία \(Α(3,2α)\) και \(Β(4,α)\) είναι
\begin{align}λ&=\frac{y_B-y_A}{x_B-x_A}\\ &=\frac{α-2α}{4-3}\\ &=\frac{-α}{1}\\ &=-α,\end{align}
οπότε η ευθεία που διέρχεται από τα σημεία \(A\) και \(B\) έχει εξίσωση
\begin{align}&y-y_A=λ(x-x_A)\\ \iff&y-2α=-α(x-3)\\ \iff&y-2α=-αx+3α\\ \iff&y=-αx+5α.\end{align}
ii) Τα σημεία \(Γ(α+1,1-α)\) και \(Δ(α,1)\) ανήκουν στην ευθεία \(ΑΒ\) αν και μόνο αν οι συντεταγμένες τους επαληθεύουν την εξίσωσή της, \(y=-αx+5α\). Έχουμε διαδοχικά
\begin{align}&1-α=-α(α+1)+5α\\ \iff&1-α=-α^2-α+5α\\ \iff&α^2-5α+1=0\\ \iff&α=\frac{5\pm\sqrt{21}}{2}\end{align}
και
\begin{align}&1=-α\cdot α+5α\\ \iff&1=-α^2+5α\\ \iff&α^2-5α+1=0\\ \iff&α=\frac{5\pm\sqrt{21}}{2}.\end{align}
iii) Είναι
\begin{align}\overrightarrow{AB}&=(x_B-x_A,y_B-y_A)\\ &=(4-3,α-2α)\\ &=(1,-α)\end{align}
και
\begin{align}\overrightarrow{ΔΓ}&=(x_Γ-x_Δ,y_Γ-y_Δ)\\ &=(α+1-α,1-α-1)\\ &=(1,-α).\end{align}
Παρατηρούμε ότι \(\overrightarrow{ΑΒ}=\overrightarrow{ΔΓ}=(1,-α)\). Όμως από το προηγούμενο ερώτημα προκύπτει ότι, όταν \(α\neq\dfrac{5\pm\sqrt{21}}{2}\), τα σημεία \(Γ\) και \(Δ\) δεν ανήκουν στην ευθεία \(AB\). Τότε, επειδή \(\overrightarrow{AB}=\overrightarrow{ΓΔ}\), τα ευθύγραμμα τμήματα \(AB\) και \(ΔΓ\) θα είναι παράλληλα και θα έχουν ίσα μήκη, οπότε το τετράπλευρο \(ΑΒΓΔ\) είναι παραλληλόγραμμο.
β) Έστω ότι το τετράπλευρο \(ΑΒΓΔ\) είναι τετράγωνο για κάποιο \(α\neq\dfrac{5\pm\sqrt{21}}{2}\). Τότε θα έχουμε \(|\overrightarrow{AΒ}|=|\overrightarrow{ΑΔ}|\). Από το προηγούμενο ερώτημα είναι \(\overrightarrow{AB}=(1,-α)\), άρα
$$|\overrightarrow{AB}|=\sqrt{1^2+(-α)^2}=\sqrt{1+α^2}.$$
Επίσης είναι
$$\overrightarrow{ΑΔ}=(x_Δ-x_A,y_Δ-y_A)=(α-3,1-2α),$$
άρα
\begin{align}|\overrightarrow{ΑΔ}|&=\sqrt{(α-3)^2+(1-2α)^2}\\ &=\sqrt{5α^2-10α+10}.\end{align}
Επομένως θα έχουμε
\begin{align}&|\overrightarrow{AB}|=|\overrightarrow{AΔ}|\\ \iff&\sqrt{1+α^2}=\sqrt{5α^2-10α+10}\\ \iff&5α^2-10α+10=1+α^2\\ \iff&4α^2-10α+9=0.\end{align}
Η τελευταία εξίσωση έχει διακρίνουσα
\begin{align}Δ&=(-10)^2-4\cdot 4\cdot 9\\ &=-44 < 0,\end{align}
άρα δεν έχει πραγματικές ρίζες. Οπότε δεν υπάρχει πραγματικός αριθμός \(α\) ώστε το τετράπλευρο \(ΑΒΓΔ\) να είναι τετράγωνο. Επομένως ο ισχυρισμός είναι ψευδής.
Θέμα: 18236
ΘΕΜΑ 2
Σε τρίγωνο \(ΑΒΓ\) είναι \(A(-1,5)\) και \(B(2,1)\). Αν οι πλευρές \(ΑΓ\) και \(ΒΓ\) βρίσκονται πάνω στις ευθείες \(ε_1:\ y=-x+4\) και \(ε_2:\ y=-\dfrac{1}{2}x+2\) αντίστοιχα, τότε:
α) Να αποδείξετε ότι \(Γ(4,0).\)
(Μονάδες 12)
β) Να βρείτε:
- το συντελεστή διεύθυνσης της ευθείας \(ΑΓ\)
(Μονάδες 6) - την εξίσωση του ύψους \(ΒΔ.\)
(Μονάδες 7)
Απάντηση Θέματος: 18236
**α)**Το σημείο \(Γ\) είναι το σημείο τομής των \(ε_1,\ ε_2\) και προσδιορίζεται από τη λύση του αντίστοιχου συστήματος. Είναι:
$$\begin{align} & \begin{cases} y=-x+4 \\ y=-\dfrac{1}{2} x+2 \end{cases} \\ \Leftrightarrow & \begin{cases} -x+4 =-\dfrac{1}{2} x+2 \\ y=-x+4 \end{cases} \\ \Leftrightarrow & \begin{cases} -2x+8 =-x+4 \\ y=-x+4 \end{cases} \\ \Leftrightarrow & \begin{cases} -x=4-8 \\ y=-x+4 \end{cases} \\ \Leftrightarrow & \begin{cases} x=4 \\ y=0 \end{cases} \end{align}$$
Οπότε \(Γ(4,0).\)
β) i. Ο συντελεστής διεύθυνσης της ευθείας \(ΑΓ\) είναι:
$$λ_{ΑΓ}=\dfrac{0-5}{4+1}=-1$$
- To ύψος \(ΒΔ\) είναι κάθετο στην πλευρά \(ΑΓ\), οπότε:
$$λ_{ΒΔ} \cdot λ_{ΑΓ}=-1 \overset{(i)}{\Rightarrow} λ_{ΒΔ}=1$$
Επομένως, η εξίσωση του ύψους \(ΒΔ\) είναι:
$$y-1=1\cdot (x-2)\Leftrightarrow y=x-1$$
Θέμα: 18351
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(-1,5),\ Β(3,3)\). Να υπολογίσετε:
α) Τις συντεταγμένες του μέσου \(Μ\) του τμήματος \(ΑΒ\).
(Μονάδες 8)
β) Το συντελεστή διεύθυνσης της ευθείας \(ΑΒ.\)
(Μονάδες 8)
γ) Την εξίσωση της μεσοκαθέτου \((η)\) του τμήματος \(ΑΒ.\)
(Μονάδες 9)
Απάντηση Θέματος: 18351
α) Το μέσο \(Μ\) του τμήματος \(ΑΒ\) είναι:
$$Μ\left( \dfrac{x_Α+x_Β}{2},\dfrac{y_Α+y_Β}{2}\right)=(1,4)$$
β) Ο συντελεστής διεύθυνσης της ευθείας \(ΑΒ\) είναι:
\(λ_{ΑΒ}=\dfrac{y_B−y_A}{x_B−x_A}=\dfrac{3−5}{3−(−1)}=\dfrac{−2}{4}=−\dfrac{1}{2}\)
γ) Για τη μεσοκάθετο \((η)\) του τμήματος \(ΑΒ\) ισχύει:
$$η\perp ΑΒ$$ $$λ_η\cdot λ_{ΑΒ}=−1$$
Επομένως, \(λ_η=2\). Η εξίσωση της μεσοκαθέτου \((η)\) του τμήματος \(ΑΒ\) είναι:
$$y−y_Μ=λ_η (x−x_M)$$ $$\Rightarrow y−4=2(x−1)$$ $$\Rightarrow y=2x+2$$
Θέμα: 18568
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(2,4)\), \(Β(-1,0)\) και \(Γ(3,-2)\).
α) Να αποδείξετε ότι τα σημεία \(Α\), \(Β\), \(Γ\) αποτελούν κορυφές τριγώνου \(ΑΒΓ\).
(Μονάδες 4)
β) Αν η ευθεία \(ΑΒ\) τέμνει τον άξονα \(y'y\) σε ένα σημείο \(Δ\) και η ευθεία \(ΑΓ\) τέμνει τον άξονα \(x'x\) σε ένα σημείο \(Ε\), τότε:
i. Να βρείτε τις συντεταγμένες των σημείων \(Δ\) και \(Ε\).
(Μονάδες 10)
ii. Να αποδείξετε ότι \(\overrightarrow{ΑΔ}=2\overrightarrow{ΔΒ}\) και \(\overrightarrow{AE}=2\overrightarrow{EΓ}\).
(Μονάδες 6)
γ) Να αποδείξετε ότι η ευθεία \(ΔΕ\) είναι παράλληλη της \(ΒΓ\).
(Μονάδες 5)
Απάντηση Θέματος: 18568
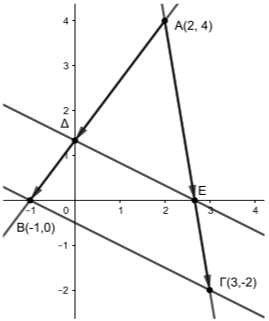
α) Οι συντελεστές διεύθυνσης των ευθειών \(ΑΒ\) και \(ΑΓ\) ορίζονται και είναι
$$λ_{ΑΒ}=\frac{y_B-y_A}{x_B-x_A}=\frac{0-4}{-1-2}=\frac{4}{3}$$
και
$$λ_{ΑΓ}=\frac{y_Γ-y_A}{x_Γ-x_A}=\frac{-2-4}{3-2}=-6.$$
Επειδή \(λ_{ΑΒ}\neq λ_{ΑΓ}\), οι ευθείες \(ΑΒ\) και \(ΑΓ\) δεν είναι παράλληλες, οπότε τα σημεία \(Α\), \(Β\) και \(Γ\) δεν είναι συνευθειακά και αποτελούν κορυφές τριγώνου.
β) Η ευθεία \(ΑΒ\) έχει συντελεστή διεύθυνσης \(\dfrac{4}{3}\) από το (α) ερώτημα και διέρχεται από το σημείο \(Α(2,4)\), άρα η εξίσωσή της είναι
\begin{align}&y-y_A=λ(x-x_A)\\ \iff&y-4=\frac{4}{3}(x-2)\\ \iff&4x-3y+4=0.\end{align}
Η ευθεία \(ΑΓ\) έχει συντελεστή διεύθυνσης \(-6\) από το (α) ερώτημα και διέρχεται από το σημείο \(Γ(3,-2)\), άρα η εξίσωσή της είναι
\begin{align}&y-y_Γ=-6(x-x_Γ)\\ \iff&y+2=-6(x-3)\\ \iff&6x+y-16=0.\end{align}
i. Στην εξίσωση της ευθείας \(ΑΒ\) θέτουμε \(x=0\) για να βρούμε το σημείο που τέμνει τον άξονα \(y'y\) και έχουμε
$$4\cdot 0-3y+4=0\iff y=\frac{4}{3}.$$
Άρα \(Δ\left(0,\dfrac{4}{3}\right)\). Ομοίως στην εξίσωση της ευθείας \(ΑΓ\) θέτουμε \(y=0\) για να βρούμε το σημείο που τέμνει τον άξονα \(x'x\) και έχουμε
$$6x+0-16=0\iff x=\frac{8}{3}.$$
Άρα \(Ε\left(\dfrac{8}{3},0\right)\).
ii. Είναι
\begin{align}\overrightarrow{ΑΔ}&= \left(0-2,\dfrac{4}{3}-4\right)\\ &=\left(-2,-\dfrac{8}{3}\right)\\ &=2\cdot \left(-1,-\dfrac{4}{3} \right)\end{align}
και
$$\overrightarrow{ΔΒ}=\left(-1-0,0-\dfrac{4}{3}\right)=\left(-1,-\dfrac{4}{3}\right),$$
οπότε προφανώς \(\overrightarrow{AΔ}=2\overrightarrow{ΔΒ}\). Για τα διανύσματα \(\overrightarrow{ΑΕ}\) και \(\overrightarrow{EΓ}\) έχουμε
\begin{align}\overrightarrow{ΑΕ}&=\left(\dfrac{8}{3}-2,0-4\right)\\ &=\left(\dfrac{2}{3},-4\right)\\ &=2\cdot \left(\dfrac{1}{3},-2\right)\end{align}
και
$$\overrightarrow{ΕΓ}=\left(3-\dfrac{8}{3},-2-0\right)=\left(\dfrac{1}{3},-2\right)$$
και ισχύει επίσης ότι \(\overrightarrow{ΑE}=2\overrightarrow{ΕΓ}\).
γ) Είναι
$$λ_{ΔΕ}=\dfrac{\dfrac{4}{3}-0}{0-\dfrac{8}{3}}=-\dfrac{1}{2}$$
και
$$λ_{ΒΓ}=\dfrac{-2-0}{3+1}=-\dfrac{2}{4}=-\dfrac{1}{2}.$$
Άρα \(λ_{ΔΕ}=λ_{ΒΓ}\), επομένως η ευθεία \(ΔΕ\) είναι παράλληλη της ευθείας \(ΒΓ\).
Θέμα: 21964
ΘΕΜΑ 2
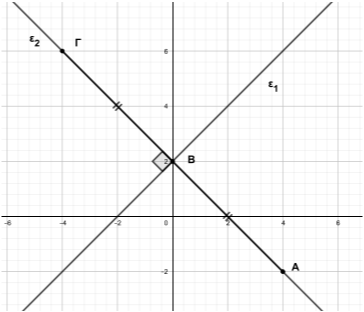
Δίνονται το σημείο \(Α(4,-2)\) και η ευθεία \((ε_1)\) με εξίσωση \(x-y+2=0\). Να βρείτε:
α) Την ευθεία \((ε_2)\) που διέρχεται από το σημείο \(Α\) και είναι κάθετη στην ευθεία \((ε_1)\).
(Μονάδες 8)
β) Το σημείο τομής \(Β\) των ευθειών \((ε_1)\) και \((ε_2):y=-x+2\).
(Μονάδες 8)
γ) Το συμμετρικό \(Γ\) του σημείου \(Α\) ως προς την ευθεία \((ε_1)\).
(Μονάδες 9)
Απάντηση Θέματος: 21964
α) Η ευθεία \((ε_1)\) έχει εξίσωση \(y=x+2\), συνεπώς έχει συντελεστή διεύθυνσης \(λ_1=1\). Η ευθεία \((ε_2)\) είναι κάθετη στην ευθεία \((ε_1)\), συνεπώς το γινόμενο των συντελεστών διεύθυνσης των δύο ευθειών θα ισούται με \(-1\), άρα \(λ_2=-1\). Επιπλέον, η ευθεία \((ε_2)\) διέρχεται από το σημείο \(Α\), άρα η εξίσωσή της θα είναι
$$\begin{align}&y-y_A=λ_2\cdot(x-x_A)\\ \iff&y-(-2)=-1\cdot(x-4)\\ \iff&y+2=-x+4\\ \iff&y=-x+2.\end{align}$$
Άρα η εξίσωση της ευθείας (\(ε_2\)) είναι \(y=-x+2\).
β) Οι συντεταγμένες του σημείου τομής \(Β\) των δύο ευθειών \((ε_1)\) και \((ε_2)\) θα προκύψουν από τη λύση του συστήματος:
\begin{align}&\begin{cases}y=x+2\\y=-x+2\end{cases}\\ \iff&\begin{cases}y=x+2\\x+2=-x+2\end{cases}\\ \iff&\begin{cases}y=x+2\\2x=0\end{cases}\\ \iff&\begin{cases}y=2\\x=0\end{cases}\end{align}
Άρα \(Β(0,2)\).
γ) Αν \(Γ\) είναι το συμμετρικό του \(Α\) ως προς το \(Β\), τότε τα σημεία \(Α\), \(Β\) και \(Γ\) είναι συνευθειακά και μάλιστα το \(Β\) είναι το μέσο του τμήματος \(ΑΓ\), άρα θα ισχύει:
\begin{align}&\begin{cases}x_B=\dfrac{x_A+x_Γ}{2}\\y_B=\dfrac{y_A+y_Γ}{2}\end{cases}\\ \iff&\begin{cases}0=\dfrac{4+x_Γ}{2}\\2=\dfrac{-2+y_Γ}{2}\end{cases}\\ \iff&\begin{cases}x_Γ=-4\\y_Γ=6\end{cases}\end{align}
Οπότε το συμμετρικό του σημείο \(Α\) ως προς την ευθεία \((ε_1)\), που ταυτίζεται με το συμμετρικό του ως προς το σημείο \(Β\), είναι το σημείο \(Γ(-4,6)\).
Θέμα: 21965
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(2,-4)\) και \(Β(0,-2)\).
α) Να βρείτε το μέσο \(Μ\) του τμήματος \(ΑΒ\).
(Μονάδες 4)
β) Να βρείτε την εξίσωση της μεσοκαθέτου \((ζ)\) του ευθύγραμμου τμήματος \(ΑΒ\).
(Μονάδες 5)
γ) Αν \((ζ):y=x-4\) και \((ε):y=2x-6\), τότε να βρείτε το σημείο τομής των ευθειών \((ζ)\), \((ε)\).
(Μονάδες 9)
δ) Να δείξετε ότι η εξίσωση του κύκλου που διέρχεται από τα σημεία \(Α\), \(Β\) και το κέντρο του ανήκει στην ευθεία \((ε)\) είναι η \((x-2)^2+(y+2)^2=4\).
(Μονάδες 7)
Απάντηση Θέματος: 21965
α) Για το μέσο \(Μ\) του τμήματος \(ΑΒ\) ισχύει
\begin{align}&M\left(\frac{x_A+x_B}{2},\frac{y_A+y_B}{2}\right)\\ \iff&M\left(\frac{2+0}{2},\frac{-4+(-2)}{2}\right)\\ \iff&M(1,-3).\end{align}
β) Η κλίση του \(ΑΒ\) είναι
\begin{align}λ_{ΑΒ}&=\frac{y_B-y_A}{x_B-x_A}\\ &=\frac{-2-(-4)}{0-2}\\ &=\frac{2}{-2}\\ &=-1.\end{align}
Η κλίση της μεσοκαθέτου \((ζ)\) του \(ΑΒ\) θα πρέπει να είναι \(λ=1\) (αφού το γινόμενο των δύο κλίσεων θα πρέπει να ισούται με \(-1\)). Η εξίσωση της μεσοκαθέτου \((ζ)\) του τμήματος \(ΑΒ\) θα είναι
\begin{align}&y-y_M=λ\cdot(x-x_M)\\ \iff&y-(-3)=1(x-1)\\ \iff&y+3=x-1\\ \iff&y=x-4.\end{align}
γ) Το σημείο τομής των ευθειών \((ε)\) και \((ζ)\) θα έχει συντεταγμένες τις λύσεις του συστήματος:
\begin{align}&\begin{cases}y=x-4\\y=2x-6\end{cases}\\ \iff&\begin{cases}y=x-4\\x-4=2x-6\end{cases}\\ \iff&\begin{cases}y=-2\\x=2\end{cases}\end{align}
Άρα το σημείο τομής των δύο ευθειών είναι το σημείο \((2,-2)\).
δ) Το κέντρο \(Κ\) του κύκλου θα πρέπει να ανήκει ταυτόχρονα στη μεσοκάθετο του τμήματος \(ΑΒ\), δηλαδή την ευθεία \((ζ)\), και στην ευθεία \((ε)\), άρα θα πρέπει να είναι το σημείο τομής τους που βρήκαμε στο ερώτημα (β), δηλαδή το \(Κ(2,-2)\). Η ακτίνα του κύκλου θα είναι \(ρ=(ΚΑ)=(ΚΒ)\), δηλαδή
\begin{align}ρ&=(ΚΒ)\\ &=\sqrt{(2-0)^2+(-2+2)^2}\\ &=\sqrt{4+0}\\ &=2.\end{align}
Η εξίσωση του κύκλου λοιπόν θα είναι
$$(x-2)^2+(y+2)^2=4.$$
Θέμα: 22071
ΘΕΜΑ 2
Οι πλευρές \(ΑΒ\) και \(ΑΔ\) ενός παραλληλογράμμου \(ΑΒΓΔ\) έχουν εξισώσεις \(x+2y+1=0\) και \(2x+y+5=0\), αντίστοιχα, και το κέντρο του παραλληλογράμμου είναι το σημείο \(Κ(1,2)\).
α) Να αποδείξετε ότι:
i. Η κορυφή \(Α\) του παραλληλογράμμου έχει συντεταγμένες \(Α(-3,1)\).
(Μονάδες 8)
ii. Η κορυφή \(Γ\) του παραλληλογράμμου έχει συντεταγμένες \(Γ(5,3)\).
(Μονάδες 7)
β) Να βρείτε τις εξισώσεις των άλλων δύο πλευρών του, \(ΒΓ\) και \(ΓΔ\).
(Μονάδες 10)
Απάντηση Θέματος: 22071
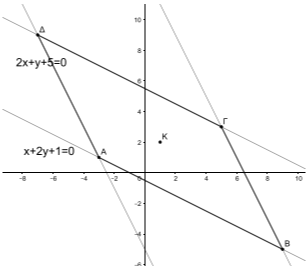
α) i. Έστω \(ΑΒΓΔ\) το παραλληλόγραμμο στο οποίο είναι \(ΑΒ: x+2y+1=0\) και \(ΑΔ:2x+y+5=0\). Το σημείο τομής των ευθειών \(ΑΒ\) και \(ΑΔ\) είναι το σημείο \(Α\), του οποίου οι συντεταγμένες προκύπτουν από τη λύση του παρακάτω συστήματος:
\begin{align}&\begin{cases}x+2y+1=0\\2x+y+5=0\end{cases}\\ \iff&\begin{cases}-2x-4y-2=0\\2x+y+5=0\end{cases}\\ \iff&\begin{cases}-3y+3=0\\2x+y+5=0\end{cases}\\ \iff&\begin{cases}y=1\\x=-3\end{cases}\end{align}
Άρα \(Α(-3,1)\).
ii. Το σημείο \(Κ\) είναι το κέντρο του παραλληλογράμμου, οπότε είναι το μέσο του τμήματος \(ΑΓ\). Αν \(Γ(x_Γ,y_Γ)\), τότε για το σημείο \(Κ\) έχουμε \(Κ\left(\dfrac{-3+x_Γ}{2},\dfrac{1+y_Γ}{2}\right)\). Όμως οι συντεταγμένες του \(Κ\) είναι \((1,2)\), οπότε
$$\frac{-3+x_Γ}{2}=1\iff x_Γ=5$$
και
$$\frac{1+y_Γ}{2}=2\iff y_Γ=3.$$
Άρα \(Γ(5,3)\).
β) Η πλευρά \(ΒΓ\) διέρχεται από το σημείο \(Γ(5,3)\) και \(ΒΓ//ΑΔ\). Η εξίσωση της ευθείας \(ΑΔ\) είναι \(2x+y+5=0\) με \(λ_{ΑΔ}=-2\). Άρα \(λ_{ΒΓ}=-2\), οπότε η εξίσωση της \(ΒΓ\) είναι
\begin{align}&y-y_Γ=-2(x-x_Γ)\\ \iff&y-3=-2(x-5)\\ \iff&2x+y-13=0.\end{align}
Η πλευρά \(ΓΔ\) διέρχεται από το \(Γ(5,3)\) και \(ΓΔ//ΑΒ\). Η εξίσωση της ευθείας \(ΑΒ\) είναι \(x+2y+1=0\) με \(λ_{ΑΒ}=-\dfrac{1}{2}\). Άρα \(λ_{ΓΔ}=-\dfrac{1}{2}\), οπότε η εξίσωση της \(ΓΔ\) είναι
\begin{align}&y-y_Γ=-\frac{1}{2}(x-x_Γ)\\ \iff&y-3=-\frac{1}{2}(x-5)\\ \iff&x+2y-11=0.\end{align}
Θέμα: 22173
ΘΕΜΑ 2
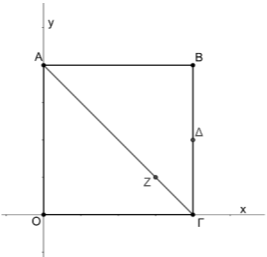
Δίνεται το τετράγωνο \(ΑΒΓΟ\) με κορυφές τα σημεία \(Α(0,4)\), \(Β(4,4)\), \(Γ(4,0)\), \(Ο(0,0)\). Στην διαγώνιο \(ΑΓ\) παίρνουμε σημείο \(Ζ\) τέτοιο ώστε \(\overrightarrow{ΑΖ}=\dfrac{3}{4}\overrightarrow{ΑΓ}\). Επίσης, θεωρούμε το μέσο \(Δ\) της \(ΒΓ\).
α) Να βρείτε:
i. Τις συντεταγμένες του σημείου \(Δ\).
(Μονάδες 7)
ii. Τις συντεταγμένες του σημείου \(Ζ\).
(Μονάδες 9)
β) Αν το σημείο \(Δ\) είναι το \((4,2)\) και το σημείο \(Ζ\) το \((3,1)\), να αποδείξετε ότι η ευθεία \(ΖΔ\) είναι κάθετη στην ευθεία \(ΑΓ\).
(Μονάδες 9)
Απάντηση Θέματος: 22173
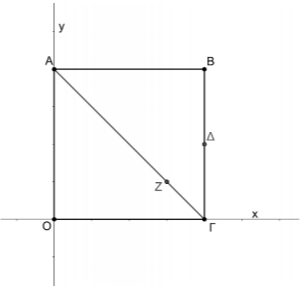
α) i. Οι συντεταγμένες του μέσου \(Δ\) του \(ΒΓ\) δίνονται από τους τύπους
\begin{align}x_Δ&=\frac{x_Γ+x_B}{2}\\ &=\frac{4+4}{2}\\ &=4\end{align}
και
\begin{align}y_Δ&=\frac{y_Γ+y_B}{2}\\ &=\frac{4+0}{2}\\ &=2.\end{align}
Επομένως, είναι \(Δ(4,2)\).
ii. Έστω \(Ζ(x,y)\). Τότε
\begin{align}\overrightarrow{AZ}&=(x_Z-z_A,y_Z-y_A)\\ &=(x-0,y-4)\\ &=(x,y-4)\end{align}
και
\begin{align}\overrightarrow{AΓ}&=(x_Γ-x_A,y_Γ-y_A)\\ &=(4-0,0-4)\\ &=(4,-4).\end{align}
Όμως \(\overrightarrow{AZ}=\dfrac{3}{4}\overrightarrow{ΑΓ}\), άρα
$$(x,y-4)=\frac{3}{4}(4,-4)=(3,-3).$$
Επομένως \(x=3\) και \(y-4=-3\), δηλαδή \(y=1\). Άρα είναι \(Ζ(3,1)\).
β) Από το ερώτημα (α) έχουμε ότι \(\overrightarrow{ΑΖ}=(3,-3)\). Επιπλέον,
\begin{align}\overrightarrow{ZΔ}&=(x_Δ-x_Z,y_Δ-y_Z)\\ &=(4-3,2-1)\\ &=(1,1).\end{align}
Επομένως είναι
\begin{align}\overrightarrow{AZ}\cdot\overrightarrow{ZΔ}&=(3,3)\cdot(1,-1)\\ &=3-3\\ &=0\end{align}
και άρα τα διανύσματα είναι κάθετα. Το ίδιο θα ισχύει και για τους φορείς τους, δηλαδή η \(ΑΓ\) είναι κάθετη στην \(ΖΔ\).
Εναλλακτική λύση:
Ο συντελεστής διεύθυνσης της ευθείας \(ΑΖ\) είναι
$$λ_{ΑΖ}=\frac{y_Z-y_A}{x_Z-x_A}=\frac{1-4}{3-0}=-1.$$
Ο συντελεστής διεύθυνσης της ευθείας \(ΖΔ\) είναι
$$λ_{ΖΔ}=\frac{y_Δ-y_Z}{x_Δ-x_Z}=\frac{2-1}{4-3}=1.$$
Επειδή \(λ_{AZ}\cdot λ_ΖΔ=-1\), οι ευθείες \(ΑΖ\) και \(ΖΔ\) είναι κάθετες.
2.2 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ
Θέμα: 14978
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(1,1), Β(3,3)\).
α) Αν \(M(x,y)\) σημείο του επιπέδου, να βρείτε τις αποστάσεις \(d_1, d_2\) του \(Μ\) από τα \(Α\) και \(Β\) αντίστοιχα.
(Μονάδες 6)
β) Να γράψετε τη σχέση που πρέπει να πληρούν οι \(d_1, d_2\), ώστε το σημείο \(Μ\) να ανήκει στη μεσοκάθετο του \(ΑΒ\).
(Μονάδες 4)
γ) Να βρείτε την εξίσωση της μεσοκαθέτου του \(ΑΒ\).
(Μονάδες 8)
δ) Να βρείτε σημείο \(Σ\) τέτοιο ώστε το τρίγωνο \(ΣΑΒ\) να είναι ισόπλευρο.
(Μονάδες 7)
Απάντηση Θέματος: 14978
α) Έστω \(M(x,y)\) σημείο του επιπέδου, τότε
$$d_1=(MA)=\sqrt{(x-1)^2+(y-1)^2}$$
και
$$d_2=(MB)=\sqrt{(x-3)^2+(y-3)^2}.$$
β) Ένα σημείο ανήκει στη μεσοκάθετο του ευθυγράμμου τμήματος \(ΑΒ\), αν και μόνο ανισαπέχει από τα άκρα του. Δηλαδή ισχύει \(d_1=d_2\).
γ) Ισχύει ότι
\begin{align}&d_1=d_2\\ \iff&\sqrt{(x-1)^2+(y-1)^2}=\sqrt{(x-3)^2+(y-3)^2}\\ \iff&(x-1)^2+(y-1)^2=(x-3)^2+(y-3)^2.\end{align}
Η τελευταία ισότητα παριστάνει τη σχέση που ικανοποιούν οι συντεταγμένες για τα σημεία τομής δύο κύκλων, με κέντρα τα \(Α(1,1)\) και \(Β(3,3)\) αντίστοιχα και ίσες ακτίνες, που αντιστοιχούν στα σημεία \(Κ, Μ\) του σχήματος, τα οποία ανήκουν στη μεσοκάθετο του \(ΑΒ\).
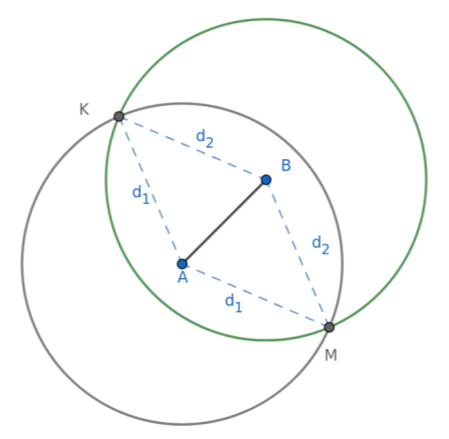
Αναπτύσσοντας την τελευταία σχέση έχουμε
\begin{align}&(x-1)^2+(y-1)^2=(x-3)^2+(y-3)^2\\ \iff&x^2-2x+1+y^2-2y+1=x^2-6x+9+y^2-6y+9\\ \iff&-2x-2y+2=-6x-6y+18\\ \iff&x+y-4=0.\end{align}
Δηλαδή όλα τα σημεία \(Μ(x,y)\) τα οποία ανήκουν στη μεσοκάθετο του ΑΒ ισοδύναμα ικανοποιούν τη σχέση \(x+y-4=0\), η οποία είναι επομένως η εξίσωση της μεσοκαθέτου του \(ΑΒ\). Εναλλακτικά, μπορεί να βρεθεί το μέσο του ευθυγράμμου τμήματος \(ΑΒ\) και στη συνέχεια η εξίσωση της ευθείας που είναι κάθετη στο \(ΑΒ\) σε αυτό το σημείο.
δ) Για να είναι το τρίγωνο \(ΣΑΒ\) ισόπλευρο, αρκεί \(ΑΒ=d_1=d_2\) δηλαδή οι κύκλοι \((A,d_1),(B,d_2)\) να έχουν ακτίνα ίση με \(ΑΒ\). Άρα
$$d_1=d_2=\sqrt{(1-3)^2+(1-3)^2}=\sqrt{4+4}=2\sqrt{2}.$$
Βρίσκουμε τα σημεία τομής του κύκλου με ακτίνα \(d_1=2\sqrt{2}\) κέντρου \(Α\) με τη μεσοκάθετο, λύνοντας το σύστημα
\begin{align}&\begin{cases}(x-1)^2+(y-1)^2=8\\x+y-4=0\end{cases}\\ \iff&\begin{cases}(x-1)^2+(4-x-1)^2=8\\y=4-x\end{cases}\\ \iff&\begin{cases}x^2-2x+1+9-6x+x^2=8\\y=4-x\end{cases}\\ \iff&\begin{cases}2x^2-8x+2=0\\y=4-x\end{cases}\\ \iff&\begin{cases}x^2-4x+1=0\\y=4-x\end{cases}\\ \iff&\begin{cases}x=\frac{4\pm\sqrt{12}}{2}\\y=4-x\end{cases}\\ \iff&\begin{cases}x=2\pm\sqrt{3}\\y=4-(2\pm\sqrt{3})\end{cases}\\ \iff&\begin{cases} (x,y)=(2+\sqrt{3},2-\sqrt{3})\\ \text{ ή }(x,y)=(2-\sqrt{3},2+\sqrt{3})\end{cases}.\end{align}
Δηλαδή βρήκαμε δύο σημεία \(Σ\), το οποίο ήταν αναμενόμενο, αφού πρόκειται για τα δύο σημεία συμμετρικά του \(ΑΒ\).
Θέμα: 15253
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$(μ^2-1)x+(3μ^2-2μ-1)y-5μ^2+4μ+1=0\quad (1)$$
όπου \(μ\in\mathbb{R}\).
α) Να βρείτε για ποιες τιμές του \(μ\) η \((1)\) παριστάνει ευθεία \((ε)\).
(Μονάδες 5)
β) Να βρείτε για ποιες τιμές του \(μ\) οι ευθείες \((ε)\):
i. είναι παράλληλες στον \(x'x\).
(Μονάδες 4)
ii. είναι παράλληλες στον \(y'y\).
(Μονάδες 4)
iii. διέρχονται από το \((0,0)\).
(Μονάδες 4)
γ) Να δείξετε ότι όλες οι ευθείες \((ε)\) που προκύπτουν από την \((1)\) διέρχονται από σταθερό σημείο.
Απάντηση Θέματος: 15253
α) Η εξίσωση \((1)\) είναι της μορφής \(Αx+Βy+Γ=0\), όπου \(Α=μ^2-1,\ Β=3μ^2-2μ-1\) και \(Γ=-5μ^2+4μ+1\). Για να παριστάνει ευθεία πρέπει οι \(Α,\ Β\) να μη γίνονται ταυτόχρονα \(0\). Έχουμε
\begin{align}&Α=0\\ \iff&μ^2-1=0\\ \iff&μ=1\text{ ή }μ=-1\end{align}
και
\begin{align}&Β=0\\ \iff&3μ^2-2μ-1=0\\ \iff&μ=1\text{ ή }μ=-\frac{1}{3}.\end{align}
Συνεπώς η \((1)\) παριστάνει ευθεία για κάθε πραγματική τιμή του \(μ\) εκτός από την τιμή \(μ=1\).
β) i. Για να είναι παράλληλη στον \(x'x\) πρέπει
$$Α=0\iff μ=\pm 1.$$
Όμως η τιμή \(μ=1\) απορρίπτεται από το (α), οπότε τελικά \(μ=-1\).
ii. Για να είναι παράλληλη στον \(y'y\) πρέπει
$$B=0\iff μ=1\text{ ή }μ=-\frac{1}{3}.$$
H τιμή \(μ=1\) απορρίπτεται, οπότε τελικά \(μ=-\dfrac{1}{3}\).
iii. Για να διέρχεται από το \((0,0)\) πρέπει
\begin{align}&Γ=0\\ \iff&-5μ^2+4μ+1=0\\ \iff&μ=1\text{ ή }μ=-\frac{1}{5}.\end{align}
H τιμή \(μ=1\) και πάλι απορρίπτεται, οπότε τελικά \(μ=-\dfrac{1}{5}\).
γ) Για \(μ=-1\) η \((1)\) γίνεται \(ε_1:4y-8=0\) ενώ για \(μ=0\) γίνεται \(ε_2:-x-y+1=0\). Οι \((ε_1)\) και \((ε_2)\) τέμνονται στο σημείο \(Μ\) με συντεταγμένες τη λύση του συστήματος
$$\begin{cases}4y-8=0\\-x-y+1=0\end{cases}\iff\begin{cases}y=2\\x=-1\end{cases}$$
οπότε \(Μ(-1,2)\).
Οι συντεταγμενες του \(Μ\) επαληθεύουν την \((1)\) για κάθε τιμή του \(μ\) αφού
\begin{align}&\phantom{{}={}}(μ^2-1)\cdot(-1)+(3μ^2-2μ-1)\cdot 2-5μ^2+4μ+1\\ &=-μ^2+1+6μ^2-4μ-2-5μ^2+4μ+1\\ &=0\end{align}
οπότε συμπεραίνουμε ότι όλες οι ευθείες που προκύπτουν από την \((1)\) διέρχονται από το σταθερό σημείο \(Μ(-1,2)\).
Θέμα: 15439
ΘΕΜΑ 4
Μία φωτεινή ακτίνα διερχόμενη από το σημείο \(A(2,3)\) και προσπίπτουσα στην ευθεία \((ε)\) με εξίσωση \(x+y+1=0\), μετά την ανάκλασή της διέρχεται από το σημείο \(M(1,1)\).
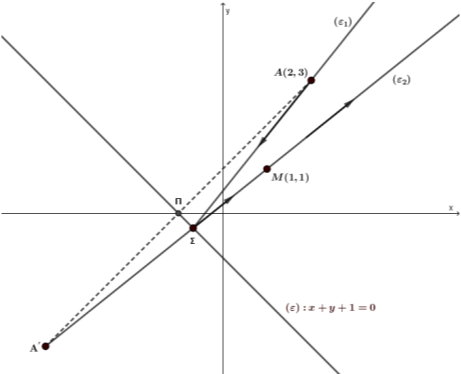
α) i. Να αποδείξετε ότι η προβολή του σημείου \(A\) πάνω στην ευθεία \((ε)\) είναι το σημείο \(Π(-1,0)\).
(Μονάδες 7)
ii. Να αποδείξετε ότι το συμμετρικό του σημείου \(A\) ως προς την ευθεία \((ε)\), είναι το σημείο \(Α'(-4,-3)\).
(Μονάδες 5)
β) i. Αν γνωρίζετε ότι η ανακλώμενη ακτίνα είναι η ευθεία \((ε_2)\), η οποία διέρχεται από τα σημεία \(Α'\), \(Σ\), \(Μ\), τότε να βρείτε την εξίσωσή της.
(Μονάδες 4)
ii. Να βρείτε τις συντεταγμένες του σημείου πρόσπτωσης \(Σ\) της φωτεινής ακτίνας \((ε_1)\) πάνω στην ευθεία \((ε)\).
(Μονάδες 5)
γ) Αν \(Σ\left(-\dfrac{2}{3},-\dfrac{1}{3}\right)\), τότε να βρείτε την εξίσωση της προσπίπτουσας ακτίνας \((ε_1)\).
(Μονάδες 4)
Απάντηση Θέματος: 15439
α) i. Αφού η κλίση της \((ε)\) είναι \(λ_ε=-1\), έχουμε \(λ_{ΑΠ}=1\) γιατί η \(ΑΠ\) είναι κάθετη στην \((ε)\). Έτσι, η \(ΑΠ\) έχει εξίσωση \(y-3=1\cdot (x-2)\), δηλαδή
$$ΑΠ:y=x+1.$$
Οι συντεταγμένες του σημείου \(Π\) προκύπτουν από την επίλυση του συστήματος:
\begin{align}&\begin{cases}y=x+1\\x+y+1=0\end{cases}\\ \iff&\begin{cases}y=x+1\\2x+2=0\end{cases}\\ \iff&\begin{cases}y=0\\x=-1\end{cases}\end{align}
Επομένως, \(Π(-1,0)\).
ii. Το \(Π\) είναι το μέσον του ευθύγραμμου τμήματος \(AA'\), και ως εκ τούτου είναι
\begin{align}&\begin{cases}\dfrac{x+2}{2}=-1\\ \dfrac{y+3}{2}=0\end{cases}\\ \iff&\begin{cases}x=-4\\y=-3\end{cases}\end{align}
δηλαδή \(A'(-4,-3)\).
β) i. Η \((ε_2)\) είναι η ευθεία που διέρχεται από τα σημεία \(Α'(-4,-3)\) και \(Μ(1,1)\), δηλαδή έχει εξίσωση
\begin{align}&y-1=\dfrac{-3-1}{-4-1}(x-1)\\ \iff&4x-5y+1=0.\end{align}
ii. Οι συντεταγμένες του σημείου \(Σ\), δηλαδή του σημείου πρόσπτωσης της φωτεινής ακτίνας πάνω στην ευθεία \((ε)\), προκύπτουν από την επίλυση του συστήματος των ευθειών \((ε)\) και \((ε_2)\):
\begin{align}&\begin{cases}x+y+1=0\\4x-5y+1=0\end{cases}\\ \iff&\begin{cases}-4x-4y-4=0\\4x-5y+1=0\end{cases}\\ \iff&\begin{cases}x+y+1=0\\-9y-3=0\end{cases}\\ \iff&\begin{cases}x-\dfrac{1}{3}+1=0\\y=-\dfrac{1}{3}\end{cases}\\ \iff&\begin{cases}x=-\dfrac{2}{3}\\y=-\dfrac{1}{3}\end{cases}\end{align}
Άρα \(Σ\left(-\dfrac{2}{3},-\dfrac{1}{3}\right)\).
γ) Η \((ε_1)\) είναι η ευθεία που διέρχεται από τα σημεία \(Α(2,3)\) και \(Σ\left(-\dfrac{2}{3},-\dfrac{1}{3}\right)\), δηλαδή έχει εξίσωση
\begin{align}&y-3=\dfrac{3+\frac{1}{3}}{2+\frac{2}{3}}(x-2)\\ \iff&5x-4y+2=0.\end{align}
Θέμα: 15475
ΘΕΜΑ 4
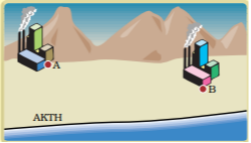
Δύο εργοστάσια \(A\) και \(B\) τα οποία σε ένα σύστημα συντεταγμένων έχουν συντεταγμένες \(A(2,1)\), \(B(4,3)\), βρίσκονται κοντά σε μια ακτή που πρόκειται να κατασκευαστεί μια αποβάθρα και θα εξυπηρετεί τα δύο εργοστάσια.
α) Να βρείτε την εξίσωση της ευθείας που συνδέει τα δύο εργοστάσια.
(Μονάδες 8)
β) Αν η ακτή είναι ευθύγραμμη με εξίσωση \(ε:y=2x-7\), να βρείτε τις συντεταγμένες του σημείου της ακτής στο οποίο πρέπει να τοποθετηθεί η αποβάθρα ώστε να απέχει εξ ίσου από τα δύο εργοστάσια.
(Μονάδες 10)
γ) Αν το ζητούμενο σημείο του ερωτήματος (β) είναι \(N(4,1)\), να βρείτε πόσο απέχει το κάθε εργοστάσιο από το σημείο αυτό.
(Μονάδες 7)
Απάντηση Θέματος: 15475
α) Η εξίσωση της ευθείας \(AB\) που συνδέει τα δύο εργοστάσια είναι
\begin{align}&y-1=\frac{3-1}{4-2}\cdot (x-2)\\ \iff&y-1=1\cdot (x-2)\\ \iff&y=x-1.\end{align}
β) Το σημείο της ακτής που απέχει εξ ίσου από τα δύο εργοστάσια είναι το σημείο τομής της ευθύγραμμης ακτής με τη μεσοκάθετο της \(AB\). Βρίσκουμε τις συντεταγμένες του μέσου \(M(x_M,y_M)\) της \(AB\). Είναι \(x_M=\dfrac{2+4}{2}=3\) και \(y_M=\dfrac{1+3}{2}=2\). Άρα \(M(3,2)\). Ο συντελεστής διεύθυνσης της \(AB\) είναι \(λ=1\). Η μεσοκάθετος \(ε'\) της \(ΑΒ\) θα έχει συντελεστή διεύθυνσης \(λ'\) για τον οποίο θα ισχύει
$$λ\cdot λ'=-1\iff λ'=-1.$$
Επομένως η εξίσωση της μεσοκαθέτου \(ε'\) είναι
$$y-2=-1(x-3)\iff y=-x+5.$$
Λύνουμε το σύστημα:
\begin{align}&\begin{cases}y=2x-7\\y=-x+5\end{cases}\\ \iff&\begin{cases}2x-7=-x+5\\y=-x+5\end{cases}\\ \iff&\begin{cases}3x=12\\y=-x+5\end{cases}\\ \iff&\begin{cases}x=4\\y=1\end{cases}\end{align}
Άρα το ζητούμενο σημείο είναι το \(N(4,1)\).
γ) Η απόσταση του καθενός από τα δύο εργοστάσια από το σημείο \(N\) της ακτής είναι
\begin{align}(BN)&=(AN)\\ &=\sqrt{(2-4)^2+(1-1)^2}\\ &=\sqrt{2^2+0^2}\\ &=2.\end{align}
Θέμα: 15986
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(1,1)\) και \(Β(2,3)\).
α) i) Να βρείτε το συντελεστή διεύθυνσης της ευθείας που διέρχεται από τα \(Α,\ Β.\)
ii) Να αποδείξετε ότι η εξίσωση της ευθείας \(ΑΒ\) είναι η \((ε): y=2x−1.\)
(Μονάδες 12)
β) Να εξετάσετε αν το σημείο \(Γ(2^{100},5)\) ανήκει στην ευθεία \((ε).\)
(Μονάδες 13)
Απάντηση Θέματος: 15986
α) i) Η ευθεία που διέρχεται από τα \(Α,\ Β\) θα έχει εξίσωση: \(y=λx+b\) αφού \(x_A≠x_B.\)
Ο συντελεστής διεύθυνσης της ευθείας είναι
$$\begin{align}λ_{ΑΒ} & =\dfrac{y_B−y_A}{x_B−x_A} \\ & =\dfrac{3−1}{2−1} \\ &=\dfrac{2}{1}\\ &=2.\end{align}$$
Άρα η ευθεία θα είναι της μορφής \(y=2x+b.\)
ii) Αντικαθιστώντας τις συντεταγμένες του σημείου \(Α\) θα έχουμε: \(1=2\cdot 1+b \Leftrightarrow b=−1\).
Επομένως, η εξίσωση της ευθείας θα είναι η \((ε):\ y=2x−1.\)
β) Αντικαθιστώντας την τεταγμένη του σημείου \(Γ\) στην εξίσωση της ευθείας \((ε)\) έχουμε: \(5=2x−1\Leftrightarrow x=3≠2^{100}\)
Άρα το σημείο \(Γ\) δεν ανήκει στην \((ε).\)
Θέμα: 16003
ΘΕΜΑ 4
Θεωρούμε την οικογένεια των ευθειών
$$ε_α:(α-4)x-2αy+α+4=0,\ α\in\mathbb{R}.$$
α) Να βρείτε τις ευθείες που προκύπτουν όταν \(α=0\) και όταν \(α=1\) και κατόπιν να προσδιορίσετε το κοινό τους σημείο \(Μ\).
(Μονάδες 8)
β) Να αποδείξετε ότι όλες οι ευθείες της οικογένειας διέρχονται από το \(Μ\).
(Μονάδες 6)
γ) Έστω ότι μια ευθεία της παραπάνω οικογένειας τέμνει τους θετικούς ημιάξονες \(Οx, Οy\) στα σημεία \(Α\) και \(Β\) αντίστοιχα.
i. Να αποδείξετε ότι \(0\lt α\lt 4\).
(Μονάδες 6)
ii. Να βρείτε για ποια τιμή του \(α\) ισχύει \((ΟΑ)=2(ΟΒ)\).
(Μονάδες 5)
Απάντηση Θέματος: 16003
α) Με \(α=0\) έχουμε
$$ε_0:-4x+4=0\iff x=1,$$
ενώ με \(α=1\) έχουμε
$$ε_1:-3x-2y+5=0.$$
Το κοινό τους σημείο προσδιορίζεται από τη λύση του συστήματος
$$\begin{cases}x=1\\3x+2y=5\end{cases}$$
Εύκολα βρίσκουμε ότι η μοναδική λύση του συστήματος είναι η \(x=1\) και \(y=1\). Άρα οι ευθείες \(ε_0,ε_1\) τέμνονται στο σημείο \(M(1,1)\).
β) Αρκεί να αποδείξουμε ότι όλες οι ευθείες διέρχονται από το σημείο \(M(1,1)\). Με \(x=y=1\) η αρχική εξίσωση γράφεται \(α-4-2α+α+4=0\) και προφανώς ισχύει. Άρα, όλες οι ευθείες της οικογένειας διέρχονται από το σημείο \(Μ\).
γ) i. Οι ευθείες που προκύπτουν όταν \(α=4\) ή \(α=0\) δεν τέμνουν και τους δυο άξονες αφού η πρώτη είναι παράλληλη στον \(x΄x\) και η δεύτερη στον \(y΄y\). Έτσι, βρίσκουμε τα κοινά σημεία των ευθειών της οικογένειας με τους άξονες, όταν \(α\neq 0\) και \(α\neq 4\). Με \(x=0\) έχουμε \(y=\dfrac{α+4}{2α}\), ενώ με \(y=0\) έχουμε \(x=-\dfrac{α+4}{α-4}\), οπότε τα κοινά σημεία με τους άξονες είναι τα \(Α\left(\dfrac{α+4}{4-α},0\right)\) και \(Β\left(0,\dfrac{α+4}{0}\right)\). Τα σημεία \(Α\) και \(Β\) βρίσκονται στους θετικούς ημιάξονες, μόνο όταν
$$\frac{α+4}{4-α}\gt 0\quad (1)$$
και
$$\frac{α+4}{2α}\gt 0.\quad (2)$$
Είναι:
\begin{align} (1) \iff&(α+4)(4-α)\gt 0\\ \iff&α^2-16\lt 0\\ \iff&α^2\lt 16\\ \iff&-4\lt α\lt 4,\end{align}
με \(α\neq0\), και
\begin{align} (2)\iff&2α(α+4)\gt 0\\ \iff&α\lt -4\text{ ή }α\gt 0,\end{align}
με \(α\neq4\). Η συναλήθευση των δυο αποτελεσμάτων δίνει \(0\lt α\lt 4\) που είναι το ζητούμενο.
ii. Όταν \(0\lt α\lt 4\), τα σημεία \(Α, Β\) είναι στους θετικούς ημιάξονες, οπότε \((ΟΑ)=\dfrac{α+4}{4-α}\) και \((ΟΒ)=\dfrac{α+4}{2α}\). Επομένως
\begin{align}&(ΟΑ)=2(ΟΒ)\\ \iff&\frac{α+4}{4-α}=2\frac{α+4}{2α}\\ \iff&α=4-α\\ \iff&α=2.\end{align}
Θέμα: 16477
ΘΕΜΑ 4
Σε καρτεσιανό σύστημα συντεταγμένων \(Oxy\), η εξίσωση ευθείας
$$ε_λ:λx+(1-λ)y+2=0,$$
όπου \(λ\) αριθμός που μεταβάλλεται στο \(\mathbb{R}\), παριστάνει τη φωτεινή ακτίνα που εκπέμπει ένας περιστρεφόμενος φάρος \(Φ\). Ακόμη δίνεται ότι ένα φορτηγό πλοίο είναι αγκυροβολημένο στο σημείο \(O(0,0)\).
α) i. Να βρείτε τις συντεταγμένες του φάρου \(Φ\).
(Μονάδες 10)
ii. Να εξετάσετε αν υπάρχει φωτεινή ακτίνα που εκπέμπεται από το φάρο προς το αγκυροβολημένο πλοίο.
(Μονάδες 5)
β) Ένα ρυμουλκό πλοίο \(P\) βρίσκεται βόρεια του φάρου \(Φ\). Η φωτεινή ακτίνα που φωτίζει το \(P\) έχει εξίσωση \(x+y+4=0\). Να βρείτε τις συντεταγμένες του σημείου \(P\) όταν είναι γνωστό ότι η συντομότερη διαδρομή που πρέπει να διανύσει το ρυμουλκό πλοίο για να πάει προς το αγκυροβολημένο φορτηγό πλοίο είναι ίση με \(4\) μονάδες μήκους.
(Μονάδες 10)
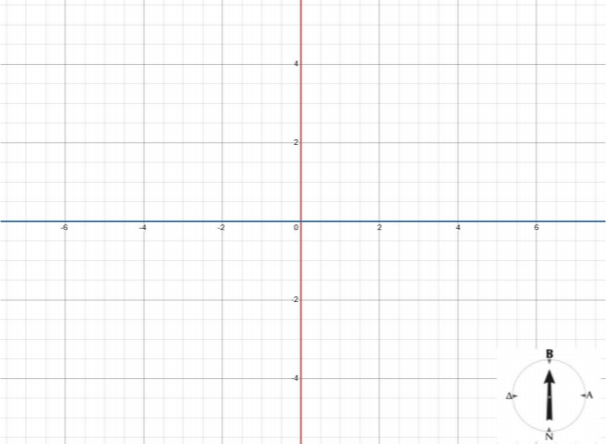
Απάντηση Θέματος: 16477
α) i. Όλες οι φωτεινές ακτίνες που παριστάνει η εξίσωση \(ε_λ\) διέρχονται από το φάρο \(Φ\). Επομένως οι συντεταγμένες του φάρου \(Φ(x_Φ,y_Φ)\) επαληθεύουν την εξίσωση της \(ε_λ\) για κάθε \(λ\in\mathbb{R}\). Δηλαδή είναι:
\begin{align}&λx_Φ+(1-λ)y_Φ+2=0\\ \iff&λx_Φ+y_Φ-λy_Φ+2=0\\ \iff&(x_Φ-y_Φ)λ+y_Φ+2=0\\ \iff&\begin{cases}x_Φ-y_Φ=0\\y_Φ+2=0\end{cases}\\ \iff&\begin{cases}x_Φ=y_Φ\\y_Φ=-2\end{cases}\\ \iff&\begin{cases}x_Φ=-2\\y_Φ=-2\end{cases}\end{align}
Οπότε οι συντεταγμένες του φάρου είναι \(Φ(-2,-2)\).
Δεύτερος τρόπος:
Γνωρίζουμε ότι όλες οι ευθείες διέρχονται από το ίδιο σημείο \(Φ\). Για τον προσδιορισμό των συντεταγμένων του φάρου αρκεί να βρούμε το σημείο τομής δυο ευθειών της οικογένειας \(ε_λ\). Μια ευθεία της οικογένειας \(ε_λ\) προκύπτει για \(λ=1\) με εξίσωση
$$1x+(1-1)y+2=0\iff x+2=0$$
και μια άλλη προκύπτει για \(λ=0\) με εξίσωση
$$0x+(1-0)y+2=0\iff y+2=0.$$
Για την εύρεση του κοινού σημείου \(Φ\) των ευθειών με εξισώσεις \(x+2=0\) και \(y+2=0\), επιλύουμε το σύστημα
$$\begin{cases}y+2=0\\x+2=0\end{cases}\iff\begin{cases}y=-2\\x=-2\end{cases}$$
Άρα οι συντεταγμένες του φάρου είναι \(Φ(-2,-2)\).
ii. Έστω ότι υπάρχει φωτεινή ακτίνα που εκπέμπεται από το φάρο προς το αγκυροβολημένο πλοίο. Άρα υπάρχει πραγματικός αριθμός \(λ\) ώστε η \(ε_λ\) να διέρχεται από το \(O(0,0)\). Τότε οι συντεταγμένες του \(O(0,0)\) επαληθεύουν την εξίσωση της \(ε_λ\). Έχουμε
$$λ\cdot 0+(1-λ)\cdot 0+2=0\iff 2=0,$$
άτοπο. Οπότε δεν υπάρχει φωτεινή ακτίνα που εκπέμπεται από το φάρο προς το αγκυροβολημένο πλοίο.
β) Αν είναι \(P(x_P,y_P)\) τότε ισχύει
$$y_P > y_Φ\iff y_P > -2$$
αφού το ρυμουλκό πλοίο \(P\) βρίσκεται βόρεια του φάρου \(Φ\). Επειδή το σημείο \(P\) ανήκει στην ευθεία με εξίσωση \(x+y+4=0\), ισχύει
$$x_P+y_P+4=0\iff x_P=-4-y_P.$$
Οπότε είναι \(P(-4-y_P,y_P)\) με \(y_P > -2\). Η συντομότερη διαδρομή που πρέπει να διανύσει το ρυμουλκό πλοίο για να πάει προς το αγκυροβολημένο φορτηγό πλοίο είναι το ευθύγραμμο τμήμα \(PO\) με μήκος \(4\) μονάδες. Είναι
\begin{align}&PO=4\\ \iff&\sqrt{(x_O-x_P)^2+(y_O-y_P)^2}=4\\ \iff&\sqrt{(0-(-4-y_P))^2+(0-y_P)^2}=4\\ \iff&\sqrt{(4+y_P)^2+y_P^2}=4\\ \iff&\sqrt{2y_P^2+8y_P+16}=4\\ \iff&\left(\sqrt{2y_P^2+8y_P+16}\right)^2=4^2\\ \iff&2y_P^2+8y_P+16=16\\ \iff&2y_P^2+8y_P=0\\ \iff&2y_P(y_P+4)=0\\ \iff&2y_P=0\text{ ή }y_P+4=0\\ \iff&y_P=0\text{ ή }y_P=-4.\end{align}
Δεκτή είναι μόνο η \(y_P=0 > -2\) αφού \(-4 < -2\). Ακόμη είναι
$$x_P=-4-y_P=-4-0=-4.$$
Τελικά, οι συντεταγμένες του ρυμουλκού πλοίου είναι \(P(-4,0)\).

Θέμα: 18244
ΘΕΜΑ 4
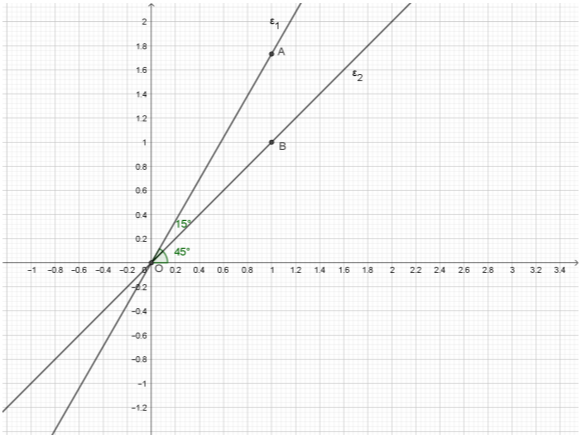
Δίνονται οι ευθείες
$$ε_1:y=\sqrt{3}x$$
και
$$ε_2:y=x.$$
α) Να σχεδιάσετε τις \(ε_1\), \(ε_2\) στο ίδιο ορθοκανονικό σύστημα αξόνων.
(Μονάδες 6)
β) Να βρείτε τη γωνία που σχηματίζει κάθε μία από τις ευθείες \(ε_1\) και \(ε_2\) με τον άξονα \(xx'\).
(Μονάδες 6)
γ) Να αιτιολογήσετε γιατί η οξεία γωνία των \(ε_1\), \(ε_2\) είναι \(15^ο\).
(Μονάδες 3)
δ) Να αποδείξετε ότι \(συν15^ο=\dfrac{\sqrt{3}+1}{2\sqrt{2}}\).
(Μονάδες 10)
Απάντηση Θέματος: 18244
α) Η \(ε_1\) διέρχεται από την αρχή των αξόνων και από το σημείο \(Α(1,\sqrt{3})\), ενώ η \(ε_2\) διέρχεται από την αρχή των αξόνων και από το σημείο \(Β(1,1)\), όπως φαίνεται στο παρακάτω σχήμα.
β) Η \(ε_1\) έχει συντελεστή διεύθυνσης \(\sqrt{3}\), οπότε σχηματίζει με τον \(xx'\) γωνία \(60^ο\), ενώ η \(ε_2\) έχει συντελεστή διεύθυνσης \(1\), οπότε σχηματίζει με τον \(xx'\) γωνία \(45^ο\).
γ) Όπως φαίνεται στο παρακάτω σχήμα, η οξεία γωνία που σχηματίζουν οι ευθείες \(ε_1\), \(ε_2\) είναι η διαφορά των γωνιών που σχηματίζει η κάθε μία από τις \(ε_1\), \(ε_2\) με τον \(xx'\), δηλαδή \(60^o-45^o=15^o\).
δ) Το \(\vec{δ}_1=(1,\sqrt{3})\) είναι παράλληλο στην ευθεία \(ε_1\) και το \(\vec{δ}_2=(1,1)\) είναι παράλληλο στην ευθεία \(ε_2\). Είναι
\begin{align}&|\vec{δ}_1|=\sqrt{1^2+(\sqrt{3})^2}=\sqrt{4}=2,\\ &|\vec{δ}_2|=\sqrt{1^2+1^2}=\sqrt{2}\end{align}
και
\begin{align}\vec{δ}_1\cdot\vec{δ}_2&=(1,\sqrt{3})\cdot (1,1)\\ &=1+\sqrt{3} > 0,\end{align}
οπότε
\begin{align}συν15^o&=συν\left(\widehat{\vec{δ}_1,\vec{δ}_2}\right)\\ &=\frac{\vec{δ}_1\cdot\vec{δ}_2}{|\vec{δ}_1|\cdot|\vec{δ}_2|}\\ &=\frac{\sqrt{3}+1}{2\sqrt{2}}.\end{align}
Θέμα: 21160
ΘΕΜΑ 4
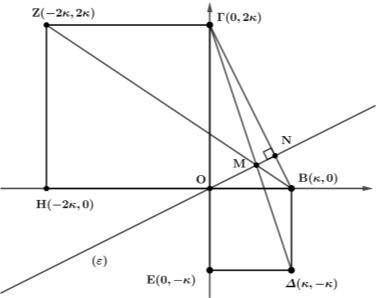
Σε καρτεσιανό σύστημα συντεταγμένων \(Οxy\) θεωρούμε το τρίγωνο που ορίζεται από τα σημεία \(Ο(0,0)\), \(Β(κ,0)\) και \(Γ(0,2κ)\) όπου \(κ\) θετικός πραγματικός αριθμός. Εξωτερικά του τριγώνου \(ΟΒΓ\) κατασκευάζουμε τετράγωνα \(ΟΒΔΕ\) και \(ΟΓΖΗ\).
α) Να βρείτε τις εξισώσεις των ευθειών που ανήκουν τα ευθύγραμμα τμήματα \(ΓΔ\) και \(ΒΖ\).
(Μονάδες 10)
β) Να βρεθεί η εξίσωση του ύψους του τριγώνου \(ΟΒΓ\) που διέρχεται από το \(Ο\).
(Μονάδες 7)
γ) Να αποδείξετε ότι οι ευθείες \(ΓΔ\), \(ΒΖ\) και το ύψος του (β) ερωτήματος διέρχονται από το ίδιο σημείο.
(Μονάδες 8)
Απάντηση Θέματος: 21160
α) Επειδή τα τετράπλευρα \(ΟΒΔΕ\) και \(ΟΓΖΗ\) είναι τετράγωνα, οι συντεταγμένες των κορυφών τους είναι \(Δ(κ,-κ)\), \(Ε(0,-κ)\), \(Ζ(-2κ,2κ)\) και \(Η(-2κ,0)\).
Η εξίσωση της ευθείας \(ΓΔ\) είναι
\begin{align}&\dfrac{y-2κ}{x-0}=\dfrac{-κ-2κ}{κ-0}\\ \iff&\dfrac{y-2κ}{x}=\dfrac{-3κ}{κ}\\ \iff&y-2κ=-3x\\ \iff&3x+y-2κ=0,\end{align}
ενώ η εξίσωση της ευθείας \(ΒΖ\) είναι
\begin{align}&\dfrac{y-2κ}{x-(-2κ)}=\dfrac{0-2κ}{κ-(-2κ)}\\ \iff&\dfrac{y-2κ}{x+2κ}=\dfrac{-2κ}{3κ}\\ \iff&3y-6κ=-2x-4κ\\ \iff&2x+3y-2κ=0.\end{align}
β) Ο συντελεστής διεύθυνσης της ευθείας που ορίζεται από το ευθύγραμμο τμήμα \(ΒΓ\) είναι
$$λ_{ΒΓ}=\frac{2κ-0}{0-κ}=-2.$$
Η ευθεία \((ε)\) που ορίζεται από το ύψος \(ΑΔ\) του ορθογωνίου τριγώνου \(ΟΒΓ\) είναι κάθετη της πλευράς \(ΒΓ\), επομένως για τους συντελεστές διεύθυνσης τους ισχύει \(λ_ε\cdot λ_{ΒΓ}=-1\). Άρα έχουμε
$$λ_ε\cdot(-2)=-1\iff λ_ε=\frac{1}{2}.$$
Η ευθεία \((ε)\) διέρχεται από την αρχή των αξόνων και έχει μορφή \(y=λ_ε\cdot x\), δηλαδή \(y=\dfrac{1}{2}x\).
γ) Για να αποδείξουμε ότι οι ευθείες που ορίζονται από τα ευθύγραμμα τμήματα \(ΓΔ\), \(ΒΖ\) και η ευθεία \((ε)\) διέρχονται από το ίδιο σημείο, αρκεί να βρούμε σημείο \(Μ\) του οποίου οι συντεταγμένες να επαληθεύουν όλες τις εξισώσεις των ευθειών. Επομένως αρκεί να αποδείξουμε ότι η τομή δύο ευθειών από τις τρεις ανήκει στην τρίτη ευθεία. Οι συντεταγμένες της τομής \(Μ\) των ευθειών \((ε)\) και \(ΓΔ\) δίνονται από την λύση του συστήματος:
\begin{align}&\begin{cases}3x+y-2κ=0\\y=\frac{1}{2}x\end{cases}\\ \iff&\begin{cases}3x+\frac{1}{2}x-2κ=0\\y=\frac{1}{2}x\end{cases}\\ \iff&\begin{cases}x=\frac{4}{7}κ\\y=\frac{2}{7}κ\end{cases}\end{align}
Επομένως \(Μ\left(\dfrac{4}{7}κ,\dfrac{2}{7}κ\right)\). Το σημείο \(Μ\) ανήκει στην ευθεία που ορίζεται από το ευθύγραμμο τμήμα \(ΒΖ\), αφού οι συντεταγμένες του επαληθεύουν την εξίσωσή της. Πράγματι,
\begin{align}&2\cdot\frac{4}{7}κ+3\cdot\frac{2}{7}κ-2κ=\frac{8}{7}κ+\frac{6}{7}κ-2κ\\ &=\frac{14}{7}κ-2κ\\ &=2κ-2κ\\ &=0.\end{align}
Επομένως οι ευθείες που ορίζονται από τα ευθύγραμμα τμήματα \(ΓΔ\), \(ΒΖ\), και η ευθεία \((ε)\) διέρχονται από το ίδιο σημείο.
Θέμα: 21162
ΘΕΜΑ 2
Δίνονται τα σημεία \(A(3,2)\) και \(Β(-1,-6)\). Να βρεθούν:
α) Οι συντεταγμένες του μέσου \(Μ\) του ευθύγραμμου τμήματος \(ΑΒ\).
(Μονάδες 8)
β) Ο συντελεστής διεύθυνσης της ευθείας που διέρχεται από τα σημεία \(Α\) και \(Β\).
(Μονάδες 8)
γ) Η εξίσωση της μεσοκαθέτου ευθείας \((ε)\) του ευθύγραμμου τμήματος \(ΑΒ\).
(Μονάδες 9)
Απάντηση Θέματος: 21162
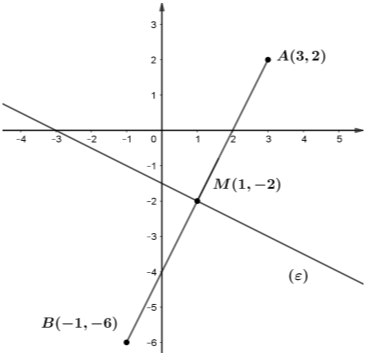
α) Το μέσο \(Μ\) του ευθυγράμμου τμήματος \(ΑΒ\) έχει συντεταγμένες
$$M\left(\frac{3+(-1)}{2},\frac{2+(-6)}{2}\right)=M(1,-2).$$
β) Ο συντελεστής διεύθυνσης της ευθείας που διέρχεται από τα σημεία \(Α\) και \(Β\) είναι
$$λ_{AB}=\frac{2-(-6)}{3-(-1)}=\frac{8}{4}=2.$$
γ) Επειδή η ευθεία \(ΑΒ\) είναι κάθετη στην ευθεία \((ε)\), έχουμε \(λ_{ΑΒ}\cdot λ_ε=-1\). Επιπλέον, από το (β), είναι \(λ_{AB}=2\), άρα
$$2\cdot λ_ε=-1\iff λ_ε=-\frac{1}{2}.$$
Επομένως η μεσοκάθετος \((ε)\) του τμήματος \(ΑΒ\) έχει εξίσωση
$$y+2=-\frac{1}{2}(x-1)\iff x+2y+3=0.$$
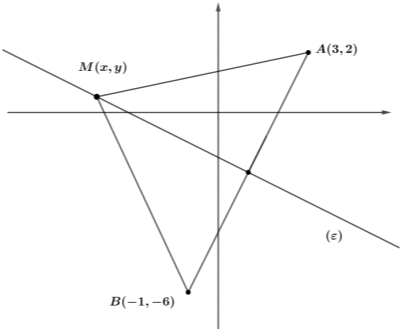
Εναλλακτική λύση
Ένα σημείο \(M(x,y)\) ανήκει στη μεσοκάθετο του ευθυγράμμου τμήματος \(ΑΒ\) αν και μόνο αν
$$\begin{align}&d(M,A)=d(M,B)\\ \iff&\sqrt{(3-x)^2+(2-y)^2}=\sqrt{(-1-x)^2+(-6-y)^2}\\ \iff&(3-x)^2+(2-y)^2=(1+x)^2+(6+y)^2\\ \iff&9-6x+x^2+4-4y+y^2=1+2x+x^2+36+12y+y^2\\ \iff&x+2y+3=0.\end{align}$$
Θέμα: 21662
ΘΕΜΑ 2
Δίνεται η ευθεία \(ε:-x+y-2=0\) και τα σημεία \(Α(-5,1)\) και \(Β(-3,5)\).
α) Να βρείτε το συμμετρικό του σημείου \(Α\) ως προς το σημείο \(Β\).
(Μονάδες 10)
β) Να βρείτε:
i. την εξίσωση της ευθείας \(ε'\) που διέρχεται από το \(Β\) και είναι κάθετη στην \(ε\).
(Μονάδες 5)
ii. το σημείο τομής των ευθειών \(ε\) και \(ε'\).
(Μονάδες 5)
iii. το συμμετρικό του σημείου \(Β\) ως προς την ευθεία \(ε\).
(Μονάδες 5)
Απάντηση Θέματος: 21662
α) 
Έστω \(Α'\) το συμμετρικό του \(Α\) ως προς το \(Β\). Τότε το σημείο \(Β\) θα είναι το μέσο του \(ΑΑ'\), οπότε:
\begin{align}&x_B=\frac{x_A+x_{A'}}{2}\\ \iff&x_{A'}=2x_B-x_A\\ \iff&x_{A'}=2\cdot(-3)-(-5)=-1\end{align}
και
\begin{align}&y_B=\frac{y_A+y_{A'}}{2}\\ \iff&y_{A'}=2y_B-y_A\\ \iff&y_{A'}=2\cdot 5-1=9.\end{align}
Άρα \(Α'(-1,9)\).
β) i. Είναι
$$λ_ε=-\frac{Α}{Β}=-\frac{-1}{1}=1.$$
και
\begin{align}&ε'\perp ε\\ \iff&λ_{ε'}\cdot λ_ε=-1\\ \iff&λ_{ε'}\cdot 1=-1\\ \iff&λ_{ε'}=-1,\end{align}
οπότε \(ε'\) έχει εξίσωση
\begin{align}&y-y_B=λ_{ε'}(x-x_B)\\ \iff&y-5=-1\cdot(x+3)\\ \iff&y=-x+2.\end{align}
ii. Έστω \(Μ\) το σημείο τομής των ευθειών \(ε\), \(ε'\). Οι συντεταγμένες του του \(Μ\) θα βρεθούν από τη λύση του συστήματος των εξισώσεων των \(ε\), \(ε'\). Είναι
$$\begin{cases}-x+y=2\\x+y=2\end{cases}\iff\begin{cases}x=0\\y=2\end{cases}$$
άρα \(Μ(0, 2)\).
iii. Αν \(Β'\) είναι το συμμετρικό του \(Β\) ως προς την ευθεία \(ε\), τότε το \(Β'\) είναι σημείο της ευθείας \(ε'\) και το \(Μ\) θα είναι το μέσο του \(ΒΒ'\), οπότε
\begin{align}&x_Μ=\frac{x_Β+x_{B'}}{2}\\ \iff&x_{B'}=2x_Μ-x_Β\\ \iff&x_{B'}=2\cdot 0-(-3)=3\end{align}
και
\begin{align}&y_Μ=\frac{y_Β+y_{B'}}{2}\\ \iff&y_{B'}=2y-y_Β\\ \iff&y_{B'}=2\cdot2-5=-1,\end{align}
άρα \(Β'(3,-1)\).
Θέμα: 22072
ΘΕΜΑ 2
Δίνονται οι εξισώσεις
$$λx+(λ-1)y-4=0\quad(1)$$
και
$$(3λ+1)x-2λy-7=0\quad(2)$$
με \(λ\in\mathbb{R}\).
α) Να αποδείξετε ότι οι εξισώσεις \((1)\) και \((2)\) παριστάνουν ευθείες για κάθε \(λ\in\mathbb{R}\).
(Μονάδες 15)
β) Να βρείτε τις τιμές του \(λ\in\mathbb{R}\), ώστε οι ευθείες με εξισώσεις \((1)\) και \((2)\) να είναι μεταξύ τους κάθετες.
(Μονάδες 10)
Απάντηση Θέματος: 22072
α) Η εξίσωση \((1)\) αποτελεί εξίσωση ευθείας αν και μόνο αν
\begin{align}&λ\neq 0\text{ ή }λ-1\neq0\\ \iff&λ\neq0\text{ ή }λ\neq 1.\end{align}
Άρα, επειδή δεν υπάρχει τιμή του \(λ\) για την οποία να μηδενίζεται και ο συντελεστής του \(x\) και ο συντελεστής του \(y\), η εξίσωση \((1)\) παριστάνει ευθεία για κάθε τιμή του \(λ\in\mathbb{R}\). Ομοίως η εξίσωση \((2)\) αποτελεί εξίσωση ευθείας αν και μόνο αν
\begin{align}&3λ+1\neq0\text{ ή }-2λ\neq0\\ \iff&λ\neq-\frac{1}{3}\text{ ή }λ\neq0.\end{align}
Άρα επειδή και πάλι δεν υπάρχει τιμή του \(λ\) για την οποία να μηδενίζεται και ο συντελεστής του \(x\) και ο συντελεστής του \(y\), η εξίσωση \((2)\) παριστάνει ευθεία για κάθε τιμή του \(λ\in\mathbb{R}\).
β) Έστω \(\vec{δ}_1=(λ-1,-λ)\) ένα διάνυσμα παράλληλο στην ευθεία με εξίσωση την \((1)\) και \(\vec{δ}_2=(-2λ,-3λ-1)\) ένα διάνυσμα παράλληλο στην ευθεία με εξίσωση την \((2)\). Οι ευθείες αυτές είναι κάθετες αν και μόνο αν
\begin{align}&\vec{δ}_1\perp\vec{δ}_2\\ \iff&\vec{δ}_1\cdot\vec{δ}_2=0\\ \iff&(λ-1)(-2λ)-λ(-3λ-1)=0\\ \iff&-2λ^2+2λ+3λ^2+λ=0\\ \iff&λ^2+3λ=0\\ \iff&λ(λ+3)=0\\ \iff&λ=0\text{ ή }λ=-3.\end{align}
Θέμα: 22092
ΘΕΜΑ 2
Δίνεται τετράπλευρο \(ΑΒΓΔ\) με κορυφή \(Α(1,4)\). Η πλευρά \(ΑΔ\) έχει εξίσωση \(3x-2y+5=0\) και η διαγώνιος \(ΒΔ\) έχει εξίσωση \(y=x+2\).
α) Να αποδείξετε ότι η κορυφή \(Δ\) έχει συντεταγμένες \(Δ(-1,1)\).
(Μονάδες 12)
β) Αν οι διαγώνιοι \(ΑΓ\) και \(ΒΔ\) του τετραπλεύρου τέμνονται κάθετα, να βρείτε την εξίσωση της διαγωνίου \(ΑΓ\).
(Μονάδες 13)
Απάντηση Θέματος: 22092
ΛΥΣΗ
α) Οι συντεταγμένες της κορυφής \(Δ\) προσδιορίζονται από τη λύση του συστήματος των εξισώσεων των ευθειών \(ΑΔ\) και \(ΒΔ\) που διέρχονται από το σημείο αυτό:
\begin{align}&\begin{cases}3x-2y+5=0\\y=x+2\end{cases}\\ \iff&\begin{cases}3x-2(x+2)+5=0\\y=x+2\end{cases}\\ \iff&\begin{cases}3x-2x-4+5=0\\y=x+2\end{cases}\\ \iff&\begin{cases}x=-1\\y=1\end{cases}\end{align}
Άρα \(Δ(-1,1)\).
β) Οι διαγώνιοι \(ΑΓ\), \(ΒΔ\) του τετραπλεύρου \(ΑΒΓΔ\) τέμνονται κάθετα, οπότε οι συντελεστές διεύθυνσης \(λ_{ΑΓ}\), \(λ_{Β∆}\) των διαγωνίων έχουν γινόμενο ίσο με \(-1\), δηλαδή \(λ_{ΑΓ} \cdot λ_{ΒΔ} = -1\). Όμως από την εξίσωση της διαγωνίου \(ΒΔ\) προκύπτει ότι \(λ_{ΒΔ}=1\), άρα \(λ_{ΑΓ}=-1\).
Η εξίσωση της διαγωνίου \(ΑΓ\) είναι επομένως
\begin{align}&y-y_A=λ_{ΑΓ}(x-x_A)\\ \iff&y-4=-1(x-1)\\ \iff&x+y-5=0.\end{align}
Θέμα: 22171
ΘΕΜΑ 2
Δίνονται οι ευθείες \(ε_1: 3x-y=5\) και \(ε_2:x-y+1=0\).
α) Να βρεθεί το σημείο τομής τους \(Μ\).
(Μονάδες 10)
β) Να βρεθεί η εξίσωση της ευθείας που διέρχεται από το σημείο \(Μ(3,4)\) και είναι κάθετη στην \((ε_2)\).
(Μονάδες 10)
γ) Να βρεθεί ένα διάνυσμα παράλληλο στην \((ε_1)\).
(Μονάδες 5)
Απάντηση Θέματος: 22171
α) Για να βρούμε το σημείο τομής λύνουμε το σύστημα των δύο εξισώσεων:
\begin{align}&\begin{cases}3x-y=5\\x=y-1\end{cases}\\ \iff&\begin{cases}3(y-1)-y=5\\x=y-1\end{cases}\\ \iff&\begin{cases}3y-3-y=5\\x=y-1\end{cases}\\ \iff&\begin{cases}2y=8\\x=y-1\end{cases}\\ \iff&\begin{cases}y=4\\x=3\end{cases}\end{align}
Επομένως το σημείο τομής είναι το \(Μ(3,4)\).
β) Η ζητούμενη ευθεία είναι κάθετη στην \((ε_2)\), οπότε το γινόμενο των συντελεστών διεύθυνσής της ζητούμενης ευθείας και της \((ε_2)\) θα είναι \(-1\). Ο συντελεστής διεύθυνσης της \((ε_2)\) είναι
$$λ_2=-\frac{A}{B}=-\frac{1}{-1}=1.$$
Επομένως ο συντελεστής διεύθυνσης \(λ\) της ζητούμενης ευθείας θα είναι \(-1\). Η ευθεία διέρχεται από το \(Μ(3,4)\), οπότε η εξίσωση θα είναι
\begin{align}&y-y_o=λ(x-x_o)\\ \iff&y-4=-1(x-3)\\ \iff&y=-x+7.\end{align}
γ) Ένα διάνυσμα παράλληλο στην \(Αx+Βy+Γ=0\) είναι το \(\vec{δ}=(Β,-Α)\), οπότε για την ευθεία \(3x-y-5=0\) ένα διάνυσμα παράλληλο σε αυτήν είναι το \(\vec{δ}=(-1,-3)\).
Θέμα: 22273
ΘΕΜΑ 4
Δίνεται η έλλειψη με εξίσωση:
$$\frac{x^2}{9}+\frac{y^2}{4}=1\quad(1)$$
α) Να προσδιορίσετε, δικαιολογώντας την απάντησή σας, τις συντεταγμένες:
i. των σημείων που η έλλειψη τέμνει τους άξονες \(x'x\) και \(y'y\),
ii. των εστιών \(Ε\) και \(Ε'\) της έλλειψης.
(Μονάδες 12)
β) Να βρείτε τις εξισώσεις των ευθειών που διέρχονται από το σημείο \(Α(0,4)\) και εφάπτονται στη καμπύλη που περιγράφει η εξίσωση \((1)\).
(Μονάδες 13)
Απάντηση Θέματος: 22273
α) Η εξίσωση \((1)\) είναι της μορφής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1\), όπου \(α^2= 9\) και \(β^2=4\).
i. Για να βρούμε τα σημεία τομής της έλλειψης αυτής με τον άξονα \(x'x\) θέτουμε στην εξίσωση \((1)\) \(y=0\). Έτσι έχουμε
$$\frac{x^2}{9}=1$$ $$\iff x^2=9$$ $$\iff x=\pm3.$$
Τα σημεία τομής με τον άξονα \(x'x\) είναι, λοιπόν, τα σημεία \(Α(3,0)\) και \(Α'(-3,0)\). Αντίστοιχα, για να βρούμε τα σημεία τομής της έλλειψης αυτής με τον άξονα \(y'y\) θέτουμε στην εξίσωση \((1)\) \(x=0\). Έτσι έχουμε
$$\frac{y^2}{4}=1$$ $$\iff y^2=4$$ $$\iff y=\pm2.$$
Επομένως, τα σημεία τομής με τον άξονα \(y'y\) είναι τα σημεία \(B(0,2)\) και \(Β'(0,-2)\).
ii. Η εξίσωση \((1)\) παριστάνει έλλειψη με εστίες στον άξονα \(x'x\). Οπότε οι εστίες έχουν συντεταγμένες \(Ε(γ,0)\) και \(Ε'(-γ,0)\), όπου \(γ=\sqrt{α^2-β^2}=\sqrt{5}\). Άρα οι εστίες της, \(Ε\) και \(Ε'\), έχουν συντεταγμένες \(Ε(\sqrt{5},0)\) και \(Ε'(-\sqrt{5},0).\)
β)
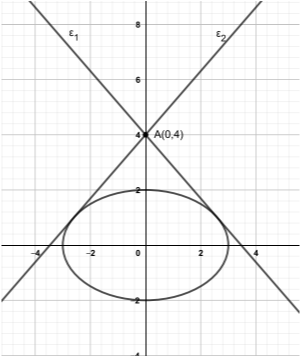
Το σημείο \(Α(0,4)\) είναι εξωτερικό σημείο της έλλειψης, αφού είναι σημείο στον άξονα \(y'y\) και η έλλειψη που μας δόθηκε τέμνει τον άξονα \(y'y\) στα σημεία \(Β(0,2)\) και \(Β'(0,-2)\). Θεωρούμε \(Μ(x_1, y_1)\) το σημείο επαφής. Η εξίσωση της εφαπτόμενης \((ε)\) στο σημείο \(Μ\) θα είναι της μορφής
$$\frac{xx_1}{9}+\frac{yy_1}{4}=1\iff 4xx_1+9yy_1=36.$$
Η ευθεία \((ε)\) διέρχεται από το σημείο \(Α(0,4)\), οπότε οι συντεταγμένες του σημείου \(Α\) επαληθεύουν την εξίσωση της ευθείας \((ε)\). Ισχύει δηλαδή
$$4\cdot0 x_1 +9\cdot 4y_1 = 36\iff y_1 = 1.$$
Επιπλέον, το σημείο \(Μ(x_1, y_1)\) είναι σημείο της έλλειψης, οπότε οι συντεταγμένες του ικανοποιούν την εξίσωση \((1)\). Άρα ισχύει
\begin{align}&\frac{x_1^2}{9}+\frac{y_1^2}{4}=1\\ \iff&\frac{x_1^2}{9}+\frac{1^2}{4}=1\\ \iff&\frac{x_1^2}{9}=\frac{3}{4}\\ \iff&x_1=\pm\frac{3\sqrt{3}}{2}.\end{align}
Για \(x_1=\dfrac{3\sqrt{3}}{2}\) και \(y_1=1\), έχουμε την εφαπτόμενη \((ε_1)\) με εξίσωση
$$4\frac{3\sqrt{3}}{2}x+9y=36\iff 2\sqrt{3}+3y=12.$$
Για \(x_1=-\dfrac{3\sqrt{3}}{2}\) και \(y_1=1\), έχουμε την εφαπτόμενη \((ε_2)\) με εξίσωση
$$4\left(-\frac{3\sqrt{3}}{2}\right)x+9y=36\iff -2\sqrt{3}x+3y=12.$$
Άρα, οι δύο εφαπτόμενες της έλλειψης που διέρχονται από το σημείο \(Α(0,4)\) είναι οι:
$$2\sqrt{3}+3y=12$$ $$\text{και } -2\sqrt{3}x+3y=12$$
2.3 ΕΜΒΑΔΟΝ ΤΡΙΓΩΝΟΥ
Θέμα: 15152
ΘΕΜΑ 3
Δίνονται τα σημεία \(Α(1,3), Β(-2,2)\) και η ευθεία \(ε: 3x+y+α=0\) με \(α\in\mathbb{R}\).
α) Να βρεθεί η απόσταση του σημείου \(Α\) από το σημείο \(Β\).
(Μονάδες 5)
β) Για ποιες τιμές του \(α\) η απόσταση \(ΑΒ\) είναι ίση με την απόσταση του σημείου \(Α\) από την ευθεία \(ε\);
(Μονάδες 8)
γ) Για \(α=4\) να βρεθεί το εμβαδόν του τριγώνου \(ΑΒΓ\), όπου \(Γ\) το σημείο τομής της ευθείας \(ε\) με τον άξονα \(y'y\).
(Μονάδες 12)
Απάντηση Θέματος: 15152
α) Κάνουμε αντικατάσταση τις συντεταγμένες των σημείων \(Α\) και \(Β\) στο τύπο της απόστασης
$$(ΑΒ)=\sqrt{(3-2)^2+(-2-1)^2}=\sqrt{10}.$$
β) Για να βρούμε τη τιμή του \(α\) θα λύσουμε την εξίσωση που προέρχεται από τη ισότητα
\begin{align}&(ΑΒ)=d(A,ε)\\ \iff&(ΑΒ)=\frac{|Αx_0+By_0+Γ|}{\sqrt{Α^2+Β^2}}\\ \iff&\sqrt{10}=\frac{|6+α|}{\sqrt{10}}\\ \iff&|α+6|=10\\ \iff&α=4\text{ ή }α=-16.\end{align}
γ) Για \(α=4\) η ευθεία \(ε\) γίνεται
$$ε: 3x+y+4=0.$$
Η ευθεία τέμνει τον \(y'y\) για \(x=0\). Άρα, το σημείο τομής της \(ε\) με τον άξονα \(y'y\) είναι το \((0,-4)\). Άρα \(Γ(0,-4)\). Επίσης, βρίσκουμε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{ΑΒ}\) και \(\overrightarrow{AΓ}\). Είναι \(\overrightarrow{ΑΒ}=(-3,-1)\) και \(\overrightarrow{ΑΓ}=(-1,-7)\). Από το τύπο του εμβαδού τριγώνου \((ΑΒΓ)=\dfrac{1}{2}|\det(\overrightarrow{ΑΒ},\overrightarrow{AΓ})|\) υπολογίζουμε ότι
\begin{align}(ΑΒΓ)&=\frac{1}{2}|\!\begin{vmatrix}-3&-1\\-1&-7\end{vmatrix}|\\ &=\frac{1}{2}\cdot 20\\ &=10\text{ τετραγωνικές μονάδες}.\end{align}
Θέμα: 15194
ΘΕΜΑ 4
Δίνονται τα σημεία του επιπέδου \(Α(1,1), Β(4,4)\) και \(Γ(3,1)\).
α) Να δείξετε ότι τα σημεία αυτά ορίζουν τρίγωνο.
(Μονάδες 7)
β) Να δείξετε ότι η μεσοκάθετος του τμήματος \(ΒΓ\) είναι η ευθεία \(ε: y=-\dfrac{1}{3}x+\dfrac{11}{3}\).
(Μονάδες 9)
γ) Να βρείτε σημείο \(Κ\) της ευθείας \((ε)\) του (β) ερωτήματος τέτοιο ώστε \((ΚΑ)=(ΚΒ)\). Τι ιδιότητα έχει το σημείο \(Κ\);
(Μονάδες 9)
Απάντηση Θέματος: 15194
ΛΥΣΗ
α) Θα δείξουμε ότι τα σημεία \(Α,Β\) και \(Γ\) δεν είναι συνευθειακά. Είναι
$$λ_{ΑΒ}=\frac{4-1}{4-1}=1$$
και
$$λ_{ΒΓ}=\frac{1-4}{3-4}=3.$$
Αφού \(λ_{ΑΒ}\neq λ_{ΒΓ}\), τα σημεία \(Α,Β\) και \(Γ\) δεν είναι συνευθειακά.
β) Για το μέσον \(Μ\) της \(ΒΓ\) έχουμε
$$x_Μ=\frac{x_Β+x_Γ}{2}=\frac{4+3}{2}=\frac{7}{2}$$
και
$$y_M=\frac{y_Β+y_Γ}{2}=\frac{4+1}{2}=\frac{5}{2}.$$
Άρα \(Μ\left(\dfrac{7}{2},\dfrac{5}{2}\right)\). Ακόμα,
\begin{align}&λ_ε\cdot λ_{ΒΓ}=-1\\ \iff&λ_ε\cdot 3=-1\\ \iff&λ_ε=-\frac{1}{3}.\end{align}
Έχουμε
$$ε:y-\frac{5}{2}=-\frac{1}{3}(x-\frac{7}{2})\iff y=-\frac{1}{3}x+\frac{11}{3}.$$
γ) Το σημείο \(Κ(x,y)\) ανήκει στην ευθεία \((ε)\) αν και μόνο αν οι συντεταγμένες του απαληθεύουν την εξίσωσή της, άρα \(Κ\left(x,-\dfrac{1}{3}x+\dfrac{11}{3}\right)\). Έχουμε
\begin{align}&(ΚΑ)=(ΚΒ)\\ \iff&\sqrt{(x-1)^2+\left(1+\frac{1}{3}x-\frac{11}{3}\right)^2}=\sqrt{(x-4)^2+\left(4+\frac{1}{3}x-\frac{11}{3}\right)^2}\\ \iff&(x-1)^2+\left(\frac{1}{3}x-\frac{8}{3}\right)^2=(x-4)^2+\left(\frac{1}{3}x+\frac{1}{3}\right)^2\\ \iff&(x-4)^2-(x-1)^2=\left(\frac{1}{3}x-\frac{8}{3}\right)^2-\left(\frac{1}{3}x+\frac{1}{3}\right)^2\\ \iff&-3(2x-5)=-3\left(\frac{2}{3}x-\frac{7}{3}\right)\\ \iff&2x-5=\frac{2}{3}x-\frac{7}{3}\\ \iff&6x-15=2x-7\\ \iff&4x=8\\ \iff&x=2.\end{align}
Οπότε
$$y=-\frac{1}{3}\cdot 2+\frac{11}{3}=3,$$
δηλαδή \(Κ(2,3)\).
Το \(Κ(2,3)\) ως σημείο της μεσοκαθέτου του \(ΒΓ\) ισαπέχει από τα άκρα του, \(Β\) και \(Γ\). Επιπλέον, \((ΚΑ)=(ΚΒ)\). Άρα τελικά \((ΚΑ)=(ΚΒ)=(ΚΓ)\), οπότε το σημείο \(Κ\) είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου \(ΑΒΓ\).
Θέμα: 15273
ΘΕΜΑ 4
Θεωρούμε τα σταθερά σημεία \(A(3,4), B(2,5)\) και \(Γ(-2,2)\) και το μεταβλητό σημείο \(Μ(4α-1,3α+1),\ α\in\mathbb{R}\).
α) Να αποδείξετε ότι τα \(Α, Β, Γ\) ορίζουν τρίγωνο.
(Μονάδες 5)
β) Να βρείτε την εξίσωση της ευθείας \(ΒΓ\).
(Μονάδες 5)
γ) Να αποδείξετε ότι τα σημεία \(Μ\) κινούνται στην ευθεία που διέρχεται από το \(Α\) και είναι παράλληλη στην \(ΒΓ\).
(Μονάδες 7)
δ) Να αποδείξετε ότι για οποιαδήποτε θέση του σημείου \(Μ\) ισχύει \((ΜΒΓ)=(ΑΒΓ)\). Πως αιτιολογείται αυτό γεωμετρικά;
(Μονάδες 8)
Απάντηση Θέματος: 15273
α) Είναι \(\overrightarrow{ΑΒ}=(-1,1)\) και \(\overrightarrow{ΑΓ}=(-5,-2)\) οπότε
$$\det(\overrightarrow{ΑΒ},\overrightarrow{ΑΓ})=\begin{vmatrix}-1&1\\-5&-2\end{vmatrix}=2+5=7\neq 0.$$
Άρα τα σημεία \(Α, Β, Γ\) δεν είναι στην ίδια ευθεία, οπότε ορίζουν τρίγωνο.
β) Η ευθεία που διέρχεται από τα σημεία \(Β, Γ\) έχει συντελεστή διεύθυνσης \(λ=\dfrac{2-5}{-2-2}=\dfrac{3}{4}\) και εξίσωση \(y-5=\dfrac{3}{4}(x-2)\) που γράφεται \(y=\dfrac{3}{4}x+\dfrac{7}{2}\).
γ) Αν \(M(x,y)\) τότε έχουμε \(x=4α-1\) και \(y=3α+1\), οπότε \(α=\dfrac{x+1}{4}\) και \(α=\dfrac{y-1}{3}\). Έχουμε λοιπόν \(\dfrac{x+1}{4}=\dfrac{y-1}{3}\) οπότε
$$y=\frac{3}{4}x+\frac{3}{4}+1=\frac{3}{4}x+\frac{7}{4}.$$
Επομένως το σημείο \(Μ\) βρίσκεται πάνω στην ευθεία \(y=\dfrac{3}{4}x+\dfrac{7}{4}\) που είναι παράλληλη στην \(ΒΓ\). Επιπλέον, με \(x=3\) έχουμε \(y=\dfrac{9}{4}+\dfrac{7}{4}=4\), οπότε η ευθεία αυτή διέρχεται από το \(Α\).
δ) Είδαμε ότι \(\det(\overrightarrow{AB},\overrightarrow{AΓ})=7\), οπότε \((ABΓ)=\dfrac{7}{2}\). Επιπλέον, \(\overrightarrow{ΒΓ}=(-4,-3)\) και \(\overrightarrow{ΒΜ}=(4α-3,3α-4)\), οπότε
\begin{align}&\phantom{{}={}}det(\overrightarrow{BΓ},\overrightarrow{ΒΜ})\\ &=\begin{vmatrix}-4&-3\\4α-3&3α-4\end{vmatrix}\\ &=-12α+16+12α-9\\ &=7\end{align}
που σημαίνει ότι \((ΜΒΓ)=\dfrac{7}{2}=(ΑΒΓ)\).
Τα εμβαδά των τριγώνων \(ΑΒΓ, ΜΒΓ\) είναι ίσα για οποιαδήποτε θέση του \(Μ\), αφού τα τρίγωνα έχουν την ίδια βάση \(ΒΓ\) και το ύψος τους \(υ\) είναι ίσο με την απόσταση των δυο παράλληλων ευθειών του σχήματος.
Θέμα: 15380
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(1,3), Β(-2,2)\) και η ευθεία \((ε): 3x+y+α=0\), με \(α\in\mathbb{R}\).
α) Να βρείτε για ποια τιμή του \(α\), η απόσταση του σημείου \(Α\) από το σημείο \(Β\) είναι ίση με την απόσταση του σημείου \(Α\) από την ευθεία \((ε)\).
(Μονάδες 8)
β) Για α=4:
i. Να βρείτε το εμβαδόν του τριγώνου \(ΑΒΓ\), όπου \(Γ\) το σημείο τομής της ευθείας \((ε)\) με τον άξονα \(y'y\).
(Μονάδες 8)
ii. Να βρείτε το σημείο της ευθείας \((ε)\) που απέχει την μικρότερη απόσταση από την αρχή των αξόνων.
(Μονάδες 9)
Απάντηση Θέματος: 15380
α) Σύμφωνα με τα δεδομένα έχουμε
\begin{align}&(ΑΒ)=d(A,ε)\\ \iff&\sqrt{(-2-1)^2+(2-3)^2}=\frac{|3\cdot 1+1\cdot 3+α|}{\sqrt{3^2+1^2}}\\ \iff&\sqrt{10}=\frac{|6+α|}{\sqrt{10}}\\ \iff&|α+6|=10\\ \iff&α+6=10\text{ ή }α+6=-10\\ \iff&α=4\text{ ή }α=-16.\end{align}
β) Για \(α=4\) έχουμε \(ε: 3x+y+4 =0\).
i. Η ευθεία \((ε)\) τέμνει τον άξονα \(y'y\) στο σημείο \(Γ\) και για \(x=0\) έχουμε \(y=-4\). Επομένως, οι συντεταγμένες του \(Γ\) είναι \((0,-4)\). Βρίσκουμε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{ΑΓ}\). Είναι \(\overrightarrow{AB}=(-3,-1)\) και \(\overrightarrow{ΑΓ}=(-1,-7)\). Από τον τύπο του εμβαδού τριγώνου \((ΑΒΓ)=\dfrac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{ΑΓ})|\) υπολογίζουμε ότι
\begin{align}(ΑΒΓ)&=\frac{1}{2}|\begin{vmatrix}-3&-1\\-1&-7\end{vmatrix}|\\ &=\frac{1}{2}\cdot 20\\ &=10\text{ τετραγωνικές μονάδες.}\end{align}
ii.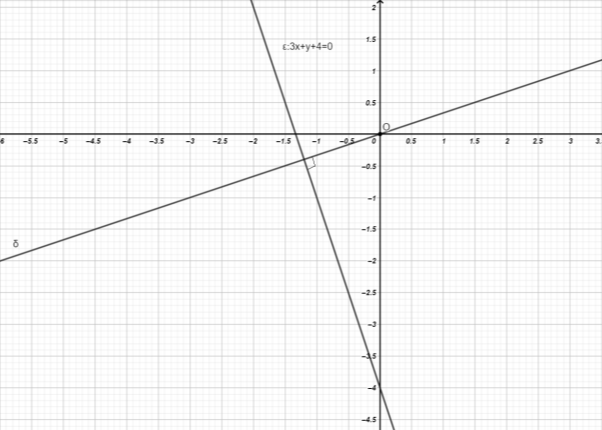
Σχεδιάζουμε σε ένα σύστημα αξόνων την ευθεία \((ε)\) και το σημείο που απέχει τη μικρότερη απόσταση από την αρχή των αξόνων, είναι το σημείο τομής της ευθείας \((ε)\) με την ευθεία \((δ)\) που είναι κάθετη στην \((ε)\) και διέρχεται από το \(Ο\).
Για να υπολογίσουμε το ζητούμενο σημείο αρκεί να βρούμε την εξίσωση της ευθείας \((δ)\) και να λύσουμε το σύστημα των δύο εξισώσεων. Επειδή \(λ_ε=-3\) και \(λ_ε\cdot λ_δ=-1\), έχουμε \(λ_δ=\dfrac{1}{3}\). Η ευθεία \((δ)\) διέρχεται από το \((0,0)\), άρα \(δ:y=\dfrac{1}{3}x\). Από τη λύση του συστήματος
\begin{cases}3x+y+4 =0\\y=\frac{1}{3}x\end{cases}
βρίσκουμε το κοινό σημείο \(\left(-\dfrac{6}{5},-\dfrac{2}{5}\right)\), που είναι το ζητούμενο.
Θέμα: 15433
ΘΕΜΑ 4
Δύο οικισμοί \(Α\) και \(Β\) βρίσκονται στις θέσεις που ορίζουν τα σημεία \(Α(-1,-2)\) και \(Β(3,1).\) Εξωτερικά των οικισμών υπάρχει ευθύγραμμος δρόμος με εξίσωση \(δ:x+y-1=0\).
α) Να βρείτε σε ποια θέση του δρόμου \((δ)\):
i. Επιτυγχάνεται η ελάχιστη απόσταση του οικισμού \(Α\) από το δρόμο.
(Μονάδες 8)
ii. Υπάρχει το Κέντρο Υγείας της περιοχής, αν είναι γνωστό ότι ισαπέχει από τους δύο οικισμούς.
(Μονάδες 7)
β) Να βρείτε τη θέση \(Γ\) ενός αυτοκινήτου πάνω στο δρόμο, αν είναι γνωστό ότι το εμβαδόν του τριγώνου που σχηματίζουν τα τρία σημεία \(Α\), \(Β\) και \(Γ\) είναι ίσο με \(8\).
(Μονάδες 10)
Απάντηση Θέματος: 15433
α) i. Για να βρούμε σε ποια θέση του δρόμου \((δ)\) ο οικισμός \(Α\) έχει τη μικρότερη απόσταση, τοποθετούμε σε ένα ορθοκανονικό σύστημα συντεταγμένων την ευθεία \(δ\) και τα σημεία \(Α\) και \(Β\). Η ευθεία \((δ)\) τέμνει τους άξονες \(x'x\) και \(y'y\) στα σημεία \((1,0)\) και \((0,1)\), αντίστοιχα.
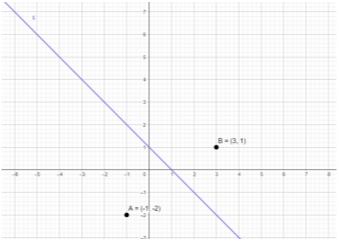
Γνωρίζουμε πως ο πιο σύντομος δρόμος που μας οδηγεί στο προορισμό μας είναι ο κάθετος δρόμος στο δρόμο που βρισκόμαστε. Έτσι, η κάθετη ευθεία στην ευθεία \((δ)\) που διέρχεται από το σημείο \(Α\) παριστάνει τον δρόμο που περνά από τον οικισμό και συναντιέται με τον δρόμο \((δ)\). Άρα, το σημείο που θα βρίσκεται η θέση που αναζητούμε είναι το σημείο τομής των δύο ευθειών.
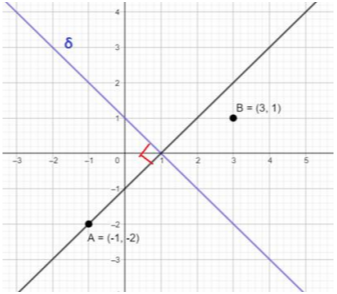
Από το σχήμα προκύπτει πως είναι το \((1,0)\). Για να το βρούμε αλγεβρικά αρκεί να προσδιορίσουμε την κάθετη ευθεία \((ε)\) στην ευθεία \((δ)\) που διέρχεται από το σημείο \(Α\). Γνωρίζουμε ότι \(δ\perp ε\) αν και μόνο αν \(λ_δ\cdot λ_ε=-1\). Είναι \(λ_δ=-1\), άρα \(λ_ε=1\). Επομένως η \((ε)\) έχει εξίσωση
$$y-(-2)=1\cdot[x-(-1)]\iff x-y-1=0.$$
Λύνοντας το σύστημα εξισώσεων των δύο ευθείων \((ε)\) και \((δ)\) βρίσκουμε το ζητούμενο σημείο:
$$\begin{cases}x+y-1=0\\x-y-1=0\end{cases}\iff\begin{cases}x=1\\y=0\end{cases}$$
ii. Για να βρούμε τη θέση του κέντρου υγείας της περιοχής που ισαπέχει από τους δύο οικισμούς ακολουθούμε το ίδιο σκεπτικό. Από τη γραφική παράσταση ψάχνουμε το σημείο της ευθεία \((δ)\) που ισαπέχει από τα \(Α\) και \(Β\), δηλαδή το σημείο Γ που βρίσκεται πάνω στην ευθεία \((δ)\) και στη μεσοκάθετο του \(ΑΒ\). Έστω σημείο \(Κ(x,y)\) που ανήκει στην ευθεία \((δ)\), άρα οι συντεταγμένες του επαληθεύουν την εξίσωση της ευθείας \((δ)\). Προσδιορίζουμε την εξίσωση της μεσοκαθέτου, \((ζ)\), του \(ΑΒ\). Είναι
$$λ_{ΑΒ}=\frac{1-(-2)}{3-(-1)}=\frac{3}{4},$$
άρα
$$λ_{ΑΒ}\cdot λ_ζ=-1\iff λ_ζ=-\frac{4}{3}.$$
Επιπλέον, το μέσο \(Μ\) του \(ΑΒ\) έχει συντεταγμένες
$$x_Μ=\frac{-1+3}{2}=1$$
και
$$y_Μ=\frac{-2+1}{2}=-\frac{1}{2}.$$
Επομένως η \((ζ)\) έχει εξίσωση
$$y+\frac{1}{2}=-\frac{4}{3}(x-1)\iff 8x+6y-5=0.$$
Λύνουμε το σύστημα των δύο εξισώσεων \((δ)\) και \((ζ)\):
$$\begin{cases}x+y-1=0\\8x+6y-5=0\end{cases}$$ $$\iff\begin{cases}x=-\frac{1}{2}\\y=\frac{3}{2}\end{cases}$$
Το σημείο \(Κ\left(-\dfrac{1}{2},\dfrac{3}{2}\right)\) είναι το ζητούμενο, δηλαδή η θέση του δρόμου \((δ)\) που βρίσκεται το κέντρο υγείας.
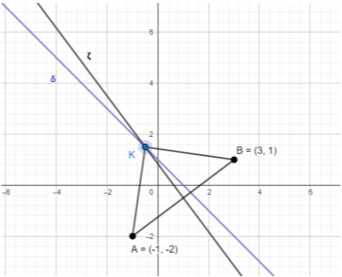
β) Το σημείο \(Γ(x,y)\) βρίσκεται πάνω στο δρόμο με εξίσωση \((δ)\), άρα είναι σημείο της ευθείας \((δ)\), δηλαδή επαληθεύει την εξίσωσή της. Επομένως \(y=1-x\) και το σημείο \(Γ\) έχει συντεταγμένες \(Γ(x,1-x)\). Βρίσκουμε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}\). Είναι \(\overrightarrow{AB}=(4,3)\) και \(\overrightarrow{AΓ}=(x+1,3-x)\). Το εμβαδόν του τριγώνου \((ΑΒΓ)\) είναι \(8\). Άρα, από τον τύπο εμβαδού τριγώνου, υπολογίζουμε
\begin{align}&(ΑΒΓ)=8\\ \iff&\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AΓ})|=8\\ \iff&\frac{1}{2}|\!\begin{vmatrix}4&3\\x+1&3-x\end{vmatrix}|=8\\ \iff&|9-7x|=16\\ \iff&x=-1\text{ ή }x=\frac{25}{7}.\end{align}
Βρίσκουμε τα αντίστοιχα \(y=2\) ή \(y=-\dfrac{18}{7}\). Επομένως, έχουμε δύο θέσεις του δρόμου που μπορεί να βρίσκεται το αυτοκίνητο και να σχηματίζει εμβαδόν \(8\), τη θέση με συντεταγμένες \((-1,2)\) και \(\left(\dfrac{25}{7},-\dfrac{18}{7}\right)\).
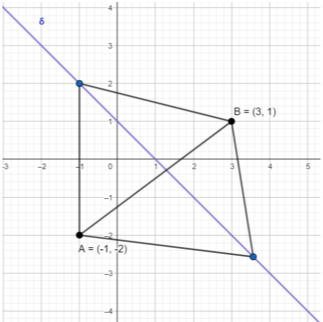
Θέμα: 15440
ΘΕΜΑ 2
Δίνονται τα σημεία \(A(0,2)\), \(B(3,0)\) και \(Γ(1,1)\).
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\), \(\overrightarrow{ΑΓ}\).
(Μονάδες 9)
β) i. Να εξετάσετε αν τα σημεία \(A\), \(B\) και \(Γ\) ορίζουν τρίγωνο.
(Μονάδες 8)
ii. Να υπολογίσετε το εμβαδόν του τριγώνου \(ΑΒΓ\).
(Μονάδες 8)
Απάντηση Θέματος: 15440
α) Oι συντεταγμένες των διανυσμάτων είναι
$$\overrightarrow{AB}=(3-0,0-2)=(3,-2)$$
και
$$\overrightarrow{AΓ}=(1-0,1-2)=(1,-1).$$
β) i. Η ορίζουσα των διανυσμάτων είναι
\begin{align}&\phantom{{}={}}\det(\overrightarrow{AB},\overrightarrow{ΑΓ})\\ &=\begin{vmatrix}3&-2\\1&-1\end{vmatrix}\\ &=-3+2\\ &=-1.\end{align}
Για να ορίζεται τρίγωνο πρέπει τα διανύσματα να μην είναι παράλληλα, διαφορετικά τα τρία σημεία θα είναι συνευθειακά. Αφού λοιπόν \(\det(\overrightarrow{AB},\overrightarrow{ΑΓ})\neq 0\), έχουμε ότι τα σημεία \(Α\), \(Β\) και \(Γ\) ορίζουν τρίγωνο.
ii. Αφού είναι \(\det(\overrightarrow{AB},\overrightarrow{AΓ})=-1\), το εμβαδόν του τριγώνου \(ΑΒΓ\) είναι
\begin{align}(ABΓ)&=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AΓ})|\\ &=\frac{1}{2}|-1|\\ &=\frac{1}{2}\text{ τ.μ.}\end{align}
Θέμα: 15681
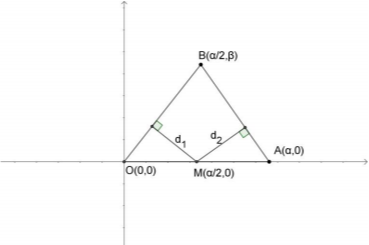
ΘΕΜΑ 4
Δίνονται τα σημεία \(Ο(0,0)\), \(Α(α,0)\), \(Β\left(\dfrac{α}{2},β\right)\) και \(Μ\left(\frac{α}{2},0\right)\), όπου \(α,\ β\) σταθεροί θετικοί πραγματικοί αριθμοί.
α) Να μεταφέρετε τα παραπάνω σημεία σε ορθοκανονικό σύστημα συντεταγμένων. Κατόπιν, να αποδείξετε ότι το τρίγωνο \(ΟΑΒ\) είναι ισοσκελές και το σημείο \(Μ\) είναι το μέσο της βάσης \(ΟΑ\).
(Μονάδες 6)
β) Να αποδείξετε ότι οι εξισώσεις των ευθειών \(ΟΒ\) και \(ΑΒ\) είναι \(ΟΒ:\ 2βx-αy=0\) και \(ΑΒ:\ 2βx+αy-2αβ=0\), αντίστοιχα.
(Μονάδες 8)
γ) Αν \(d_1\) είναι η απόσταση του σημείου \(Μ\) από την ευθεία \(ΟΒ\) και \(d_2\) η απόσταση του σημείου \(Μ\) από την ευθεία \(ΑΒ\), να αποδείξετε ότι \(d_1=d_2\).
(Μονάδες 8)
δ) Ποια πρόταση της Ευκλείδειας Γεωμετρίας έχει αποδειχθεί.
(Μονάδες 3)
Απάντηση Θέματος: 15681
α) Αφού \(β\neq 0\), τα σημεία \(Ο,Α,Β\) δεν είναι συνευθειακά. Το τρίγωνο \(ΟΑΒ\) είναι ισοσκελές με βάση \(ΟΑ\) αφού
\begin{align}(OB)&=\sqrt{\left(\frac{α}{2}-0\right)^2+(β-0)^2}\\ &=\sqrt{\frac{α^2}{4}+β^2}\end{align}
και
\begin{align}(AB)&=\sqrt{\left(\frac{α}{2}-α\right)^2+(β-0)^2}\\ &=\sqrt{\frac{α^2}{4}+β^2}.\end{align}
Εναλλακτικά, το σημείο \(Β\left(\dfrac{α}{2},β\right)\) ανήκει στη μεσοκάθετο του \(ΟΑ\), οπότε ισαπέχει από τα σημεία \(Ο\) και \(Α\). Τέλος, το μέσο του \(ΟΑ\) είναι το σημείο \(Μ\left(\dfrac{α}{2},0\right)\), αφού οι συντεταγμένες του \(Μ\) είναι ίσες με το ημιάθροισμα των συντεταγμένων των \(Ο\) και \(Α\).
β) Είναι \(α\neq 0\), οπότε
\begin{align}&ΟΒ:\ y-0=\frac{β-0}{\frac{α}{2}-0}\cdot(x-0)\\ \iff&y=\frac{2β}{α}\cdot x\\ \iff&2βx-αy=0\end{align}
και
\begin{align}&AB:\ y-0=\frac{β-0}{\frac{α}{2}-α}\cdot (x-α)\\ \iff&y=\frac{β}{-\frac{α}{2}}\cdot (x-α)\\ \iff&y=-\frac{2β}{α}\cdot (x-α)\\ \iff&2βx+αy-2αβ=0.\end{align}
γ) Είναι
\begin{align}d_1&\overset{\hphantom{α,β >0}}{=}\frac{|2β\frac{α}{2}-α\cdot 0|}{\sqrt{(2β)^2+α^2}}\\ &\overset{α,β >0}{=}\frac{αβ}{\sqrt{4β^2+α^2}}\end{align}
και
\begin{align}d_2&\overset{\hphantom{α,β >0}}{=}\frac{|2β\frac{α}{2}+α\cdot 0-2αβ|}{\sqrt{(2β)^2+α^2}}\\ &\overset{\hphantom{α,β >0}}{=}\frac{|-αβ|}{\sqrt{4β^2+α^2}}\\ &\overset{α,β >0}{=}\frac{αβ}{\sqrt{4β^2+α^2}},\end{align}
οπότε πράγματι \(d_1=d_2\).
δ) Η πρόταση της Ευκλείδειας Γεωμετρίας που αποδείχθηκε είναι η εξής:
Σε κάθε ισοσκελές τρίγωνο, το μέσο της βάσης ισαπέχει από τις ίσες πλευρές.
Θέμα: 15987
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(1,1)\) και \(Β(2,3)\).
α) Να αποδείξετε ότι η εξίσωση της ευθείας \(ΑΒ\) είναι η \((ε): y=2x-1\).
(Μονάδες 8)
β) Να αιτιολογήσετε αν το σημείο \(Γ(2^{100},5)\) ανήκει ή όχι στο ημιεπίπεδο που ορίζεται από την ευθεία \((ε)\) και την αρχή των αξόνων \(Ο(0,0)\).
(Μονάδες 8)
γ) Να αιτιολογήσετε αν το εμβαδόν του τριγώνου \(ΑΒΓ\) είναι μεγαλύτερο ή μικρότερο από το εμβαδόν του τριγώνου \(ΑΟΒ\).
(Μονάδες 9)
Απάντηση Θέματος: 15987
α) Η ευθεία που διέρχεται από τα \(Α, Β\) θα έχει εξίσωση της μορφής \(y=λx+b\) αφού \(x_A\neq x_B\). Είναι
\begin{align}λ_{ΑΒ}&=\frac{y_B-y_A}{x_B-x_A}\\ &=\frac{3-1}{2-1}\\ &=\frac{2}{1}\\ &=2.\end{align}
Άρα η ευθεία θα είναι της μορφής \(y=2x+b\). Αντικαθιστώντας τις συντεταγμένες του σημείου \(Α\) θα έχουμε
$$1=2\cdot 1+b\iff b=-1.$$
Επομένως, η εξίσωση της ευθείας θα είναι η \((ε): y=2x-1\).
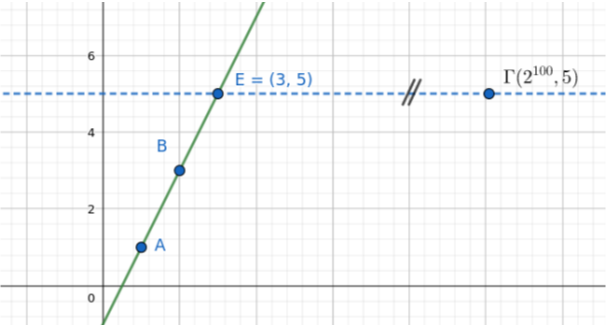
β) α' τρόπος:
Το σημείο \(E(3,5)\) ανήκει στην \((ε)\), διότι \(2\cdot 3-1=5\). Το σημείο \(Γ\) βρίσκεται στην ίδια ευθεία παράλληλη στον άξονα \(x'x\), την \(y=5\), με το \(Ε\) και «δεξιά» από την \((ε)\), ενώ το σημείο \(Ο(0,0)\) βρίσκεται στο άλλο ημιεπίπεδο, «αριστερά» από την \((ε)\), όπως βλέπουμε και στο επόμενο σχήμα.
β΄ τρόπος:
Για \(y=0\), το σημείο \(Δ\left(\dfrac{1}{2},0\right)\) ανήκει στην ευθεία \((ε)\) και το διάνυσμα \(\overrightarrow{ΔΟ}=\left(\dfrac{-1}{2},0\right)\) είναι παράλληλο στον άξονα \(x'x\). Επίσης, το σημείο \(E(3,5)\) ανήκει στην \((ε)\), διότι \(2\cdot 3-1=5\) και το διάνυσμα \(\overrightarrow{ΕΓ}=(2^{100}-3,0)\) είναι παράλληλο στον άξονα \(x'x\). Τα διανύσματα \(\overrightarrow{OΔ},\overrightarrow{EΓ}\) έχουν αρχή στην ευθεία \((ε)\) και είναι αντίρροπα, οπότε ανήκουν σε διαφορετικά ημιεπίπεδα της \((ε)\). Συνεπώς και τα σημεία \(Ο, Γ\) δεν ανήκουν στο ίδιο ημιεπίπεδο από αυτά που ορίζει η \((ε)\).
γ) Τα τρίγωνα \(ΑΟΒ\) και \(ΑΒΓ\) έχουν την ίδια βάση \(ΑΒ\), με φορέα την ευθεία \((ε)\). Η απόσταση του \(Ο\) και του \(Γ\), αντίστοιχα, από την \((ε)\) είναι:
\begin{align}d(O,ε)&=\frac{|2\cdot 0-0-1|}{\sqrt{2^2+1^2}}\\ &=\frac{1}{\sqrt{5}}\end{align}
και
\begin{align}d(Γ,ε)&=\frac{|2\cdot2^{100}-5-1|}{\sqrt{2^2+1^2}}\\ &=\frac{2^{101}-6}{\sqrt{5}} > \frac{1}{\sqrt{5}}.\end{align}
Συνεπώς \(d(O,ε) < d(Γ,ε)\), άρα το τρίγωνο \(ΑΒΓ\) έχει μεγαλύτερο εμβαδόν από το \(ΑΟΒ\).
Θέμα: 16057
ΘΕΜΑ 4
Δίνονται τα σημεία \(A(2,0)\), \(B(3,4)\) και \(λ\in\mathbb{R}\).
α) i. Να βρείτε την εξίσωση που περιγράφει όλες τις ευθείες που διέρχονται από το σημείο \(A\) και έχουν κλίση \(λ\).
(Μονάδες 5)
ii. Να αποδείξετε οτι η ευθεία, η οποία διέρχεται από το σημείο \(A\), έχει κλίση \(λ\) και απέχει απόσταση ίση με \(1\) από το σημείο \(B\), έχει εξίσωση
$$ε: 15x-8y-30=0.$$
(Μονάδες 8)
β) Να αποδείξετε οτι υπάρχει και άλλη ευθεία \((ζ)\), εκτός από την \((ε)\), η οποία διέρχεται από το σημείο \(Α\) και απέχει απόσταση ίση με \(1\) από το σημείο \(Β\).
(Μονάδες 5)
γ) Να βρείτε τις εξισώσεις των διχοτόμων των γωνιών που σχηματίζουν οι ευθείες \((ε)\) και \((ζ)\).
(Μονάδες 7)
Απάντηση Θέματος: 16057
α) i. Οι ευθείες που έχουν κλίση \(λ\) και διέρχονται από το σημείο \(Α(2,0)\) ορίζονται από την εξίσωση:
$$ε_λ:y-0=λ(x-2)\iff λx-y-2λ=0\quad(1)$$
ii. Για την απόσταση του σημείου \(B\) απο τις ευθείες \((ε_λ)\), είναι
$$d(B,ε_λ)=\frac{|3λ-4-2λ|}{\sqrt{λ^2+1}}=\frac{λ-4}{\sqrt{λ^2+1}}.$$
Επομένως, έχουμε
\begin{align}&d(B,ε_λ)=1\\ \iff&\frac{|λ-4|}{\sqrt{λ^2+1}}=1\\ \iff&|λ-4|=\sqrt{λ^2+1}\\ \iff&(λ-4)^2=λ^2+1\\ \iff&λ=\frac{15}{8}.\end{align}
Απο την \((1)\) έχουμε
\begin{align}&\frac{15}{8}x-y-\frac{30}{8}=0\\ \iff&15x-8y-30=0.\end{align}
β) Από το σημείο \(A(2,0)\) διέρχεται επίσης η κατακόρυφη ευθεία \((ζ)\), για την οποία δεν ορίζεται συντελεστής διεύθυνσης, με εξίσωση \(x=2\). Έτσι, έχουμε
$$d(Β,ζ)=\frac{|1\cdot 3+0\cdot 4-2|}{\sqrt{1}}=1.$$
γ) Οι ευθείες \((ε)\) και \((ζ)\) τέμνονται, διότι έχουν κοινό σημείο το \(Α\), αλλά δεν ταυτίζονται αφού \(λ_ε=\frac{15}{8}\) και \(ζ//y'y\). Το σημείο \(B\) απέχει ίση απόσταση από τις ευθείες \((ε)\) και \((ζ)\), επομένως ανήκει στη διχοτόμο της γωνίας των δύο ευθειών. Επιπλέον ισχύει οτι
$$λ_{ΑΒ}=\frac{4-0}{3-2}=4.$$
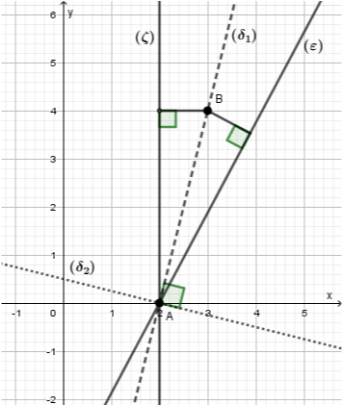
Επομένως, η μία εκ των δύο διχοτόμων \((δ_1)\), είναι η ευθεία \(ΑΒ\) με εξίσωση
$$y-0=4(x-2)\iff y=4x-8.$$
Η άλλη διχοτόμος \((δ_2)\) είναι κάθετη στην \(ΑΒ\), επομένως
$$λ_{δ_2}\cdot λ_{ΑΒ}=-1\iff λ_{δ_2}=-\frac{1}{4}.$$
Επιπλέον, διέρχεται από το σημείο \(A(2,0)\), οπότε έχει εξίσωση
$$y-0=-\frac{1}{4}(x-2)\iff y=-\frac{1}{4}x+\frac{1}{4}.$$
Θέμα: 16194
ΘΕΜΑ 2
Δίνονται οι ευθείες
\begin{align}&ε_1:8x+y-28=0,\\ &ε_2:x-y+1,\\ &ε_3:3x+4y+5=0.\end{align}
α) Να βρείτε τις συντεταγμένες του σημείου τομής \(Μ\) των \((ε_1)\) και \((ε_2)\).
(Μονάδες 9)
β) Αν το σημείο τομής είναι το \(Μ(3,4)\) να υπολογίσετε:
i. Το μέτρο του διανύσματος \(\overrightarrow{ΟΜ}\), όπου \(Ο\) η αρχή των αξόνων.
(Μονάδες 8)
ii. Την απόσταση του σημείου \(Μ\) από την ευθεία \((ε_3)\).
(Μονάδες 8)
Απάντηση Θέματος: 16194
α) Προσθέτουμε κατά μέλη τις εξισώσεις των δύο ευθειών
\begin{cases}8x+y=28\\x-y=-1\end{cases}
και παίρνουμε \(9x = 27\), άρα \(x=3\). Αντικαθιστούμε στην \(x-y=-1\) το \(x=3\) και έχουμε \(y=4\). Άρα \(Μ(3,4)\).
β) i. Είναι \(Ο(0,0)\), άρα
$$\overrightarrow{OM}=(3-0, 4-0)=(3,4)$$
και
$$|\overrightarrow{ΟΜ}|=\sqrt{3^2+4^2}=\sqrt{25}=5.$$
ii.
\begin{align}d(M,ε_3)&=\frac{|Αx_0+Βx_0+Γ|}{\sqrt{A^2+B^2}}\\ &=\frac{|3\cdot 3+4\cdot 4+5|}{\sqrt{3^2+4^2}}\\ &=\frac{30}{5}\\ &=6.\end{align}
Θέμα: 16425
ΘΕΜΑ 2
Δίνονται οι ευθείες
$$ε_1: y=\frac{2}{3}x+1$$
και
$$ε_2: x=\frac{3}{2}y+9.$$
α) Να αποδείξετε ότι \(ε_1\parallel ε_2\).
(Μονάδες 12)
β) Να υπολογίσετε την απόσταση των ευθειών \(ε_1\) και \(ε_2\).
(Μονάδες 13)
Απάντηση Θέματος: 16425
α) Είναι
$$ε_1: y=\frac{2}{3}x+1$$
με \(λ_{ε_1}=\dfrac{2}{3}\). Επίσης, η εξίσωση της \((ε_2)\) γράφεται
\begin{align}&x=\frac{3}{2}y+9\\ \iff&2x=3y+18\\ \iff&2x-3y-18=0,\end{align}
με
$$λ_{ε_2}=-\frac{Α}{Β}=-\frac{2}{-3}=\frac{2}{3}.$$
Οπότε \(λ_{ε_1}=λ_{ε_2}\), άρα \(ε_1\parallel ε_2\).
β) Από την εξίσωση της \(ε_1\), για \(x = 3\) βρίσκουμε \(y = 3\), οπότε συμπεραίνουμε ότι \(Α(3,3)\in ε_1\), επομένως
\begin{align}d(ε_1, ε_2)&=d(Α, ε_2)\\ &=\frac{|2\cdot 3-3\cdot 3-18|}{\sqrt{2^2+(-3)^2}}\\ &=\frac{|-21|}{\sqrt{13}}\\ &=\frac{21}{\sqrt{13}}\\ &=\frac{21\sqrt{13}}{13}.\end{align}
Θέμα: 16759
ΘΕΜΑ 2
Δίνονται οι ευθείες \((ε_1), (ε_2)\) και \((ε_3)\) με εξισώσεις \(x-2y=-1\), \(2x+y=4\) και \(y=-1\) αντίστοιχα.
α) Να αποδείξετε ότι οι ευθείες \((ε_1)\) και \((ε_2)\) είναι κάθετες.
(Μονάδες 8)
β) Να αποδείξετε ότι οι ευθείες \((ε_1)\) και \((ε_2)\) τέμνονται στο σημείο \(Α\left(\dfrac{7}{5},\dfrac{6}{5}\right)\).
(Μονάδες 9)
γ) Να υπολογίσετε την απόσταση του σημείου \(Α\) από την ευθεία \((ε_3)\).
(Μονάδες 8)
Απάντηση Θέματος: 16759
ΛΥΣΗ
α) Η ευθεία \((ε_1)\) έχει εξίσωση \(x-2y+1=0\) και συντελεστή διεύθυνσης
$$λ_1=-\frac{Α}{Β}=-\frac{1}{-2}=\frac{1}{2}.$$
Η ευθεία \((ε_2)\) έχει εξίσωση \(2x+y-4=0\) και συντελεστή διεύθυνσης
$$λ_2=-\frac{Α}{Β}=-\frac{2}{1}=-2.$$
Παρατηρούμε ότι \(λ_1λ_2=\dfrac{1}{2}(-2)=-1\). Άρα, οι ευθείες \((ε_1)\) και \((ε_2)\) είναι κάθετες.
β) Για το σημείο τομής των ευθειών \((ε_1)\) και \((ε_2)\), λύνουμε αρχικά την εξίσωση \(x-2y+1=0\) ως προς \(x\), οπότε \(x=2y-1\). Αντικαθιστούμε στην εξίσωση \(2x+y-4=0\) και έχουμε διαδοχικά
\begin{align}&2(2y-1)+y-4=0\\ \iff&4y-2+y-4=0\\ \iff&5y=6\\ \iff&y=\frac{6}{5}.\end{align}
Τότε είναι
$$x=\frac{12}{5}-1=\frac{7}{5}.$$
Άρα, το σημείο τομής των \((ε_1)\) και \((ε_2)\) είναι \(Α\left(\dfrac{7}{5},\dfrac{6}{5}\right)\).
γ) Η απόσταση του σημείου \(Α\) από την ευθεία \((ε_3)\) με εξίσωση \(y+1=0\) είναι
$$d(Α,ε_3)=\frac{|0\cdot\frac{7}{5}+\frac{6}{5}+1|}{\sqrt{0^2+1^2}}=\frac{11}{5}$$.
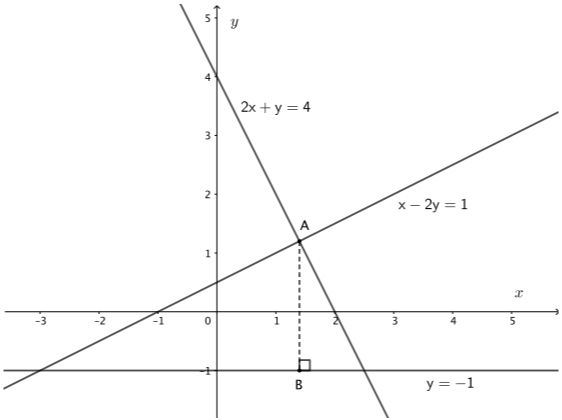
Θέμα: 16769
ΘΕΜΑ 2
Δίνεται τρίγωνο \(ΑΒΓ\) με κορυφές \(Α(1,7), Β(-1,5)\) και \(Γ(3,3)\).
α) Να υπολογίσετε το εμβαδόν του τριγώνου \(ΑΒΓ\).
(Μονάδες 9)
β) Αν \(Μ\) είναι το μέσο της πλευράς \(ΒΓ\), τότε να υπολογίσετε:
i. Τις συντεταγμένες του \(Μ\).
ii. Την εξίσωση της διαμέσου \(ΑΜ\).
(Μονάδες 16)
Απάντηση Θέματος: 16769
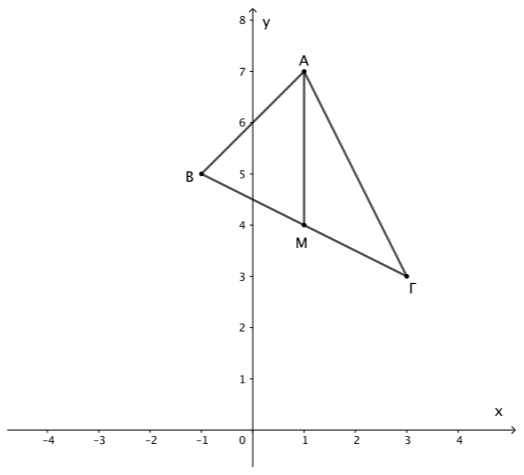
α) Το εμβαδόν του τριγώνου \(ΑΒΓ\) είναι:
$$(ΑΒΓ)=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{ΒΓ})|$$
όπου
$$\overrightarrow{ΑΒ}=(x_B-x_A,y_B-y_A)=(-1-1,5-7)=(-2,-2)$$
και
$$\overrightarrow{ΒΓ}=(x_Γ-x_B,y_Γ-y_B)=(3+1,3-5)=(4,-2).$$
Οπότε:
$$(ΑΒΓ)=\frac{1}{2}|\begin{vmatrix}-1&-2\\4&-2\end{vmatrix}|=\frac{1}{2}|4+8|=6.$$
β) i. Το μέσο \(Μ\) της πλευράς \(ΒΓ\) είναι:
$$M\left(\frac{x_B+x_Γ}{2},\frac{y_B+y_Γ}{2}\right)=(1,4).$$
ii. Παρατηρούμε ότι για τα σημεία \(Α\) και \(Μ\) είναι \(x_Μ=x_A=1\). Επομένως, η ευθεία \(ΑΜ\) είναι κατακόρυφη (δεν ορίζεται ο συντελεστής διεύθυνσης της ευθείας), οπότε έχει εξίσωση \(x=1\).
Θέμα: 16771
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(2,1), Γ(4,-1)\) και το διάνυσμα \(\overrightarrow{AB}=(3,-1)\).
α) Να βρεθεί το σημείο \(Β\).
(Μονάδες 9)
β) Αν \(Β(5,0)\):
i. Να δείξετε ότι τα σημεία \(Α, Β\) και \(Γ\) ορίζουν τρίγωνο.
(Μονάδες 8)
ii. Να υπολογίσετε το εμβαδόν του τριγώνου \(ΑΒΓ\).
(Μονάδες 8)
Απάντηση Θέματος: 16771
α) Είναι:
\begin{align}&\overrightarrow{ΑΒ}=(x_B-x_A,y_B-y_A)\\ \iff&(3,-1)=(x_B-2,y_B-1)\\ \iff&\begin{cases}x_B-2=3\\y_B-1=-1\end{cases}\\ \iff&\begin{cases}x_B=5\\y_B=0\end{cases}.\end{align}
Άρα \(B(5,0)\).
β) i. Είναι
$$\begin{align} \overrightarrow{ΑΓ} &=(x_Γ-x_A,y_Γ-y_A)\\ &=(4-2,-1-1)\\ &=(2,-2)\end{align}$$
και
$$\overrightarrow{AB}=(3,-1)$$
Για να ορίζουν τρίγωνο αρκεί: \(\det(\overrightarrow{AB},\overrightarrow{ΑΓ})\neq 0\).
Πράγματι,
$$\begin{vmatrix}3&-1\\2&-2\end{vmatrix}=3(-2)-2(-1)=-6+2=-4.$$
Επομένως, τα σημεία \(Α, Β\) και \(Γ\) ορίζουν τρίγωνο.
ii. Το εμβαδόν του τριγώνου \(ΑΒΓ\) δίνεται από τον τύπο:
$$(ΑΒΓ)=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AΓ})|=\frac{1}{2}|-4|=\frac{1}{2}\cdot 4=2.$$
Θέμα: 16774
ΘΕΜΑ 2
Δίνεται τρίγωνο \(ΑΒΓ\) με κορυφές τα σημεία \(Α(2,5), Β(3,6)\) και \(Γ(-1,-2)\).
α) Να βρείτε τον συντελεστή διεύθυνσης της ευθείας \(ΒΓ\).
(Μονάδες 7)
β) Να βρείτε την εξίσωση του ύψους που άγεται από το \(Α\).
(Μονάδες 9)
γ) Να βρείτε την γωνία που σχηματίζει η ευθεία \(ΑΒ\) με τον άξονα \(x'x\).
(Μονάδες 9)
Απάντηση Θέματος: 16774
α) Ο συντελεστής διεύθυνσης της ευθείας \(ΒΓ\) θα είναι:
\begin{align}λ_{ΒΓ}&=\frac{y_Γ-y_B}{x_Γ-x_B}\\ &=\frac{-2-6}{-1-3}\\ &=\frac{-8}{-4}\\ &=2.\end{align}
β) Έστω \(ΑΚ\) το ύψος από το \(Α\). Τότε \(AK\perp ΒΓ\), οπότε \(λ_{ΑΚ}λ_{ΒΓ}=-1\). Άρα
$$λ_{ΑΚ}\cdot 2=-1\iff λ_{ΑΚ}=-\frac{1}{2}.$$
Η εξίσωση της ευθείας \(ΑΚ\) θα είναι:
\begin{align}&y-y_A=λ_{AK}(x-x_A)\\ \iff&y-5=-\frac{1}{2}(x-2)\\ \iff&y=-\frac{1}{2}x+1+5\\ \iff&y=-\frac{1}{2}x+6.\end{align}
γ) Ο συντελεστής διεύθυνσης της ευθείας \(ΑΒ\) είναι
\begin{align}λ_{ΑΒ}&=\frac{y_B-y_A}{x_B-x_A}\\ &=\frac{6-5}{3-2}\\ &=\frac{1}{1}\\ &=1\end{align}
και ισούται με την εφαπτομένη της γωνίας που σχηματίζει η \(ΑΒ\) με τον \(xx'\), δηλαδή \(λ_{ΑΒ}=εϕω=1\), άρα \(ω=\dfrac{π}{4}\).
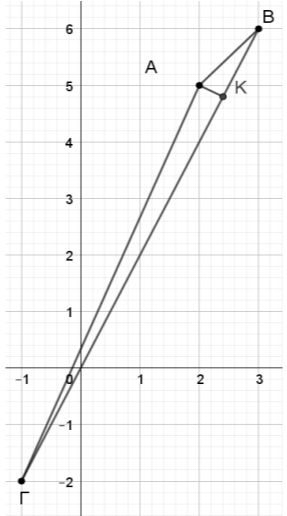
Θέμα: 16810
ΘΕΜΑ 2
Σε ορθοκανονικό σύστημα συντεταγμένων θεωρούμε τα σημεία \(Α(1,1), Β(5,2), Γ(0,-2)\) και \(Δ(8,0)\).
α) Να τοποθετήσετε τα παραπάνω σημεία του επιπέδου σε ένα πρόχειρο σχήμα και να αποδείξετε ότι το τετράπλευρο με κορυφές τα σημεία αυτά είναι τραπέζιο..
(Μονάδες 10)
β) Να υπολογίσετε το εμβαδόν του ταπεζίου του ερωτήματος (α).
(Μονάδες 15)
Απάντηση Θέματος: 16810
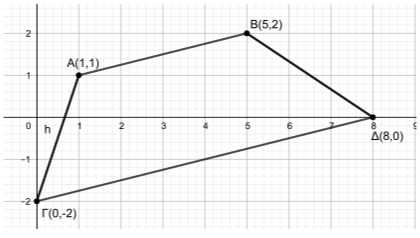
α) Τοποθετούμε τα σημεία στο επίπεδο όπως φαίνεται στο παραπάνω σχήμα. Για να είναι το τετράπλευρο \(ΑΒΓΔ\) τραπέζιο αρκεί να αποδείξουμε ότι οι πλευρές \(ΑΒ\) και \(ΓΔ\) είναι παράλληλες και οι πλευρές \(ΑΓ,ΒΔ\) τέμνονται. Είναι
$$λ_{ΑΒ}=\frac{2-1}{5-1}=\frac{1}{4}$$
και
$$λ_{ΓΔ}=\frac{0+2}{8-0}=\frac{1}{4}.$$
Άρα \(ΑΒ//ΓΔ\). Επίσης
$$λ_{ΑΓ}=\frac{-2-1}{0-1}=3$$
και
$$λ_{ΒΔ}=\frac{0-2}{8-1}=-\frac{2}{7}.$$
Άρα \(λ_{ΑΓ}\neq λ_{ΒΔ}\) και οι ευθείες \(ΑΓ\) και \(ΒΔ\) δεν είναι παράλληλες.
β) Για το εμβαδόν του τραπεζίου \(ΑΒΓΔ\) έχουμε:
$$(ΑΒΓΔ)=(ΑΒΔ)+(ΑΓΔ)\quad (1)$$
Για τα εμβαδά των τριγώνων \(ΑΒΔ\) και \(ΑΓΔ\) υπολογίζουμε πρώτα τα διανύσματα \(\overrightarrow{ΑΓ},\overrightarrow{ΑΔ}\) και \(\overrightarrow{ΑΒ}\) και έχουμε:
\begin{align}&\overrightarrow{AΓ}=(0-1,-2-1)=(-1,-3),\\ &\overrightarrow{ΑΔ}=(8-1,0-1)=(7,-1),\\ &\overrightarrow{AB}=(5-1,2-1)=(4,1),\\ &\det(\overrightarrow{ΑΓ},\overrightarrow{ΑΔ})=\begin{vmatrix}-1&-3\\7&-1\end{vmatrix}=22,\\ &\det(\overrightarrow{ΑΒ},\overrightarrow{ΑΔ})=\begin{vmatrix}4&1\\7&-1\end{vmatrix}=-11,\\ &(ΑΒΓ)=\frac{1}{2}|\det(\overrightarrow{ΑΒ},\overrightarrow{ΑΔ})|=\frac{11}{2}\end{align}
και
$$(ΑΓΔ)=\frac{1}{2}|\det(\overrightarrow{ΑΓ},\overrightarrow{ΑΔ})|=11.$$
Οπότε η σχέση \((1)\) γίνεται:
$$(ΑΒΓΔ)=\frac{11}{2}+11=\frac{33}{2}$$
Θέμα: 17694
ΘΕΜΑ 4
Στο χάρτη μίας πεδινής περιοχής, που είναι εφοδιασμένος με ορθοκανονικό σύστημα συντεταγμένων, δύο κωμοπόλεις \(Α\) και \(Β\) έχουν συντεταγμένες \(Α(3,6)\) και \(Β(7,-2)\).
α) Ανάμεσα στις δύο κωμοπόλεις, θα κατασκευαστεί ευθεία σιδηροδρομική γραμμή, κάθε σημείο της οποίας θα ισαπέχει από αυτές. Να βρείτε την εξίσωση της ευθείας, πάνω στην οποία βρίσκεται η σιδηροδρομική γραμμή.
(Μονάδες 12)
β) Πάνω στην σιδηροδρομική γραμμή θα κατασκευαστεί σταθμός \(Σ\), ώστε το εμβαδόν της περιοχής που ορίζεται από τα σημεία \(Α\), \(Β\) και \(Σ\) να ισούται με \(20\) τετραγωνικές μονάδες. Να βρείτε τις συντεταγμένες του σταθμού \(Σ\) στο χάρτη.
(Μονάδες 13)
Απάντηση Θέματος: 17694
α) Εφόσον τα σημεία της ευθείας \((ε)\) πάνω στην οποία βρίσκεται η σιδηροδρομική γραμμή ισαπέχουν από τα \(Α\), \(Β\), αυτή θα είναι η μεσοκάθετος του ευθυγράμμου τμήματος \(ΑΒ\). Αν \(Μ\) το μέσο του \(ΑΒ\), τότε
\begin{align}&x_M=\frac{x_A+x_B}{2}=\frac{3+7}{2}=5,\\ &y_M=\frac{y_A+y_B}{2}=2,\end{align}
άρα \(Μ(5, 2)\). Επίσης
$$λ_{ΑΒ}=\frac{y_Β-y_Α}{x_Β-x_Α}=\frac{-2-6}{7-3}=-2,$$
οπότε
\begin{align}&ε\perp ΑΒ\\ \iff&λ_ε\cdot λ_{ΑΒ}=-1\\ \iff&λ_ε=\frac{-1}{λ_{ΑΒ}}=\frac{-1}{-2}=\frac{1}{2},\end{align}
άρα εξίσωση της \((ε)\) είναι
\begin{align}&y-y_M=λ_ε(x-x_M)\\ \iff&y-2=\frac{1}{2}(x-5)\\ \iff&2y-4=x-5\\ \iff&x-2y-1=0.\end{align}
β) Θέλουμε
$$(ΣΑΒ) = 20\quad (1)$$
Αν \(Σ(x, y)\), τότε
\begin{align}&Σ\in ε\\ \iff&x-2y-1=0\\ \iff&x=2y+1\quad(2)\end{align}
οπότε \(Σ(2y +1, y)\). Ακόμη,
\begin{align}\overrightarrow{AB}&=(x_Β-x_Α, y_Β-y_Α)\\ &= (7-3,-2-6)\\ &= (4, -8)\end{align}
και
\begin{align}\overrightarrow{ΑΣ}&=(x_Σ-x_Α, y_Σ-y_Α)\\ &=(2y+1-3, y-6)\\ &=(2y-2, y-6),\end{align}
οπότε από την \((1)\) είναι
\begin{align}&\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{ΑΣ})|=20\\ \iff&|\begin{vmatrix}4&-8\\2y-2&y-6\end{vmatrix}|=40\\ \iff&|4(y-6)-(-8)(2y-2)|=40\\ \iff&|4y-24+16y-16|=40\\ \iff&|20y-40|=40\\ \iff&20|y-2|=40\\ \iff&|y-2|=2\\ \iff&y-2=\pm2\\ \iff&y=0\text{ ή }y=4.\end{align}
Για \(y=0\) από την \((2)\) παίρνουμε \(x=1\). Για \(y=4\) από την \((2)\) παίρνουμε \(x=9\). Άρα \(Σ(1, 0)\) ή \(Σ(9, 4)\).
Θέμα: 17695
ΘΕΜΑ 4
Υποθέτουμε, ότι σε ένα επίπεδο που έχουμε εφοδιάσει με ορθοκανονικό σύστημα συντεταγμένων, κινούνται δύο σημεία \(Α\) και \(Β\). Κάθε χρονική στιγμή \(t\), με \(t\geq 0\), η θέση του πρώτου σημείου είναι \(Α(t-1, 2t-1)\) και του δευτέρου \(Β(3t-1,-4t-1)\).
α) Να βρείτε τις εξισώσεις των γραμμών πάνω στις οποίες κινούνται τα δύο σημεία.
(Μονάδες 8)
β) Υπάρχει χρονική στιγμή κατά την οποία τα δύο σημεία ταυτίζονται;
(Μονάδες 7)
γ) Να υπολογιστεί η απόσταση των δύο σημείων την χρονική στιγμή \(t=2\).
(Μονάδες 5)
δ) Να βρεθεί η χρονική στιγμή \(t\) κατά την οποία η απόσταση του σημείου \(Α\) από την ευθεία \(ε: 4x+3y+7=0\) ισούται με \(6\).
(Μονάδες 5)
Απάντηση Θέματος: 17695
α) Έχουμε \(Α(t-1,2t-1)\), \(t\geq 0\). Αν \(Α(x, y)\) τότε
\begin{align}&\begin{cases}x=t-1\\y=2t-1\\t\geq 0\end{cases}\\ \iff&\begin{cases}t=x+1\\y=2(x+1)-1\\x+1\geq0\end{cases}\\ \iff&\begin{cases}t=x+1\\y=2x+1\\x\geq -1\end{cases}\end{align}
άρα το σημείο \(Α\) κινείται στην ημιευθεία
$$ε_1: y=2x+1\text{ με } x\geq -1.$$
Επίσης έχουμε \(Β(3t-1,-4t-1)\), \(t\geq 0\). Αν \(Β(x, y)\) τότε
\begin{align}&\begin{cases}x=3t-1\\y=-4t-1\\t\geq0\end{cases}\\ \iff&\begin{cases}t=\frac{x+1}{3}\\y=-4\frac{x+1}{3}-1\\\frac{x+1}{3}\geq0\end{cases}\\ \iff&\begin{cases}t=\frac{x+1}{3}\\3y=-4x-7\\x\geq-1\end{cases}\\ \iff&\begin{cases}t=\frac{x+1}{3}\\4x+3y+7=0\\x\geq-1\end{cases}\end{align}
άρα το σημείο \(Β\) κινείται στην ημιευθεία
$$ε_2: 4x+3y+7=0,\text{ με } x\geq -1.$$
β) Αν υπάρχει χρονική στιγμή \(t\geq 0\), κατά την οποία τα σημεία \(Α\) και \(Β\) ταυτίζονται θα είναι
\begin{align}&\begin{cases}x_Α=x_Β\\y_Α=y_Β\\t\geq 0\end{cases}\\ \iff&\begin{cases}t-1=3t-1\\2t-1=-4t-1\\t\geq 0\end{cases}\\ \iff&\begin{cases}t=0\\t=0\\t\geq 0\end{cases}\\ \iff&t=0,\end{align}
άρα τη χρονική στιγμή \(t=0\) τα σημεία \(Α\), \(Β\) ταυτίζονται.
γ) Για \(t=2\) είναι \(Α(1, 3)\) και \(Β(5, -9)\), οπότε
\begin{align}(ΑΒ)&=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\\ &=\sqrt{(5-1)^2+(-9-3)^2}\\ &=\sqrt{4^2+(-12)^2}\\ &=\sqrt{16+144}\\ &=\sqrt{160}\\ &=4\sqrt{10}.\end{align}
δ) Eίναι
\begin{align}&d(Α, ε) = 6\\ \iff&\frac{|4\cdot(t-1)+3\cdot(2t-1)+7|}{\sqrt{4^2+3^2}}=6\\ \iff&\frac{|10t|}{5}=6\\ \iff&|10t|=30\\ \iff&|t|=3\\ \iff&t=\pm3,\end{align}
αλλά \(t\geq 0\), οπότε \(t=3\) είναι η ζητούμενη χρονική στιγμή.
Θέμα: 17805
ΘΕΜΑ 2
Δίνεται το τρίγωνο \(AOB\) με \(A(3,4)\), \(B(7,1)\), \(O\) η αρχή των αξόνων, και το σημείο \(Δ\left(\dfrac{12}{5},\dfrac{16}{5}\right)\) της πλευράς \(AO\).
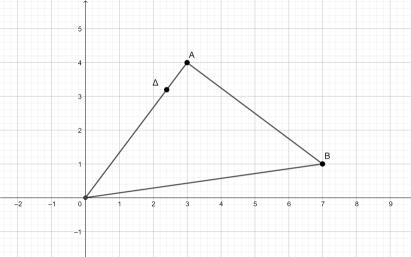
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{OA}\) και \(\overrightarrow{AΔ}\).
(Μονάδες 7)
β) Να δείξετε ότι \(\overrightarrow{AΔ}=-\dfrac{1}{5}\overrightarrow{OA}\).
(Μονάδες 9)
γ) Δίνεται ότι \((OAB)=\dfrac{25}{2}\). Να δείξετε ότι \((ΑΔΒ)=\dfrac{1}{5}(OAB)\).
(Μονάδες 9)
Απάντηση Θέματος: 17805
α) Είναι σύμφωνα με το σχήμα \(\overrightarrow{OA}=(3,4)\). Ακόμα
\begin{align}\overrightarrow{AΔ}&=(x_Δ-x_A,y_Δ-y_A)\\ &=\left(\frac{12}{5}-3,\frac{16}{5}-4\right)\\ &=\left(-\frac{3}{5},-\frac{4}{5}\right).\end{align}
β) Έχουμε
$$\begin{align}\overrightarrow{ΑΔ}&=\left(-\frac{3}{5},-\frac{4}{5}\right)\\ &=-\frac{1}{5}(3,4)\\ &=-\frac{1}{5}\overrightarrow{OA}\end{align}$$
γ) Είναι
$$\overrightarrow{AB}=(x_B-x_A,y_B-y_A)=(4,-3).$$
Έχουμε
\begin{align}(AΔB)&\overset{\phantom{\textbf{(β)}}}{=}\frac{1}{2}|\det(\overrightarrow{AΔ},\overrightarrow{AB})|\\ &\overset{\textbf{(β)}}{=}\frac{1}{2}|\!\begin{vmatrix}-\frac{3}{5}&-\frac{4}{5}\\4&-3\end{vmatrix}|\\ &\overset{\phantom{\textbf{(β)}}}{=}\frac{1}{2}|\frac{9}{5}+\frac{16}{5}|\\ &\overset{\phantom{\textbf{(β)}}}{=}\frac{5}{2}.\end{align}
Έχει δοθεί \((OAB)=\dfrac{25}{2}\), επομένως
$$(ΑΔΒ)=\frac{5}{2}=\frac{1}{5}\cdot\frac{25}{2}=\frac{1}{5}(OAB).$$
Θέμα: 18240
ΘΕΜΑ 2
Δίνεται το σημείο \(Α(1,2)\) και η ευθεία
$$ε: y=x+3.$$
α) Να βρείτε την απόσταση του σημείου \(Α\) από την ευθεία \((ε)\).
(Μονάδες 7)
β) Να βρείτε την εξίσωση της ευθείας \((η)\) που διέρχεται από το \(Α\) και είναι παράλληλη στην \((ε)\).
(Μονάδες 8)
γ) Να σχεδιάσετε στο ίδιο ορθοκανονικό σύστημα συντεταγμένων τις ευθείες \((η)\), \((ε)\).
(Μονάδες 10)
Απάντηση Θέματος: 18240
α) Είναι
$$ε: y=x+3\iff x-y+3=0,$$
οπότε
\begin{align}d(A,ε)&=\frac{|1-2+3|}{\sqrt{1^2+1^2}}\\ &=\frac{2}{\sqrt{2}}\\ &=\sqrt{2}.\end{align}
β) Είναι \((η)\parallel (ε)\), οπότε \(λ_η=λ_ε=1\), και αφού η \((η)\) διέρχεται από το \(Α(1,2)\), θα έχει εξίσωση
$$y-2=1\cdot(x-1)\iff y=x+1.$$
γ) Οι ευθείες \((η)\), \((ε)\) φαίνονται στο παρακάτω σχήμα.
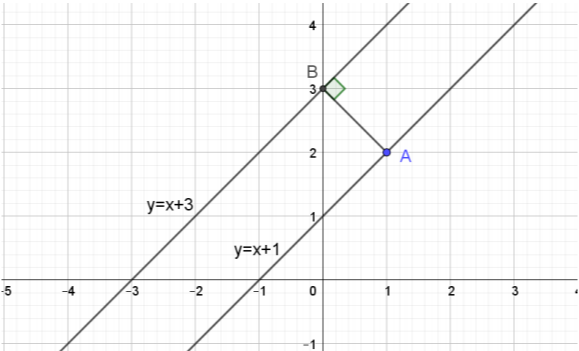
Θέμα: 18979
ΘΕΜΑ 2
Δίνονται οι ευθείες \(ε_1:2x+3y=5\) και \(ε_2:4x+6y=8\).
α) Να δείξετε ότι οι ευθείες \(ε_1\), \(ε_2\) είναι παράλληλες.
(Μονάδες 10)
β) Να αποδείξετε ότι το σημείο \(Α(1,1)\) είναι σημείο της ευθείας \(ε_1\).
(Μονάδες 5)
γ) Να βρείτε την απόσταση του σημείου \(Α\) από την ευθεία \(ε_2\).
(Μονάδες 10)
Απάντηση Θέματος: 18979
α) Οι ευθείες \(ε_1\), \(ε_2\) έχουν ίσους συντελεστές διεύθυνσης, με \(λ_1=-\dfrac{2}{3}\) και \(λ_2=-\dfrac{4}{6}=-\dfrac{2}{3}\). Άρα οι ευθείες είναι παράλληλες.
β) Οι συντεταγμένες του σημείου \(A(1,1)\) επαληθεύουν την εξίσωση της ευθείας \(ε_1\), αφού \(2\cdot 1+3\cdot 1=5\). Άρα το σημείο \(A\) ανήκει στην ευθεία \(ε_1\).
γ) Είναι
\begin{align}d(A,ε_2)&=\dfrac{|Αx_0+Βy_0+Γ|}{\sqrt{Α^2+Β^2}}\\ &=\dfrac{|4\cdot 1+6\cdot 1-8|}{\sqrt{4^2+6^2}}\\ &=\dfrac{2}{\sqrt{52}}\\ &=\dfrac{2}{\sqrt{4\cdot 13}}\\ &=\dfrac{2\sqrt{13}}{2\sqrt{13}\cdot\sqrt{13}}\\ &=\dfrac{\sqrt{13}}{13},\end{align}
αφού \(ε_2:4x+6y-8=0\).
Θέμα: 20885
ΘΕΜΑ 2
Η ευθεία \(ε\) διέρχεται από το σημείο \(Α(-3,-1)\) και σχηματίζει με τον άξονα \(x'x\) γωνία \(\dfrac{3π}{4}\).
α) Να βρείτε την εξίσωση της ευθείας \(ε\).
(Μονάδες 12)
β) Να αποδείξετε ότι το εμβαδό του τριγώνου που σχηματίζει η ευθεία \(ε\) με τους άξονες \(x'x\) και \(y'y\) είναι \(E=8\).
(Μονάδες 13)
Απάντηση Θέματος: 20885
α) Εφόσον η \(ε\) σχηματίζει με τον άξονα \(x'x\) γωνία \(\dfrac{3π}{4}\), θα είναι \(λ=εφ\dfrac{3π}{4}=-1\), οπότε η \(ε\) θα έχει εξίσωση
\begin{align}&y-y_A=λ(x-x_A)\\ &y+1=-1(x+3)\\ &y=-x-3-1\\ &y=-x-4.\end{align}
β) Από την εξίσωση της ευθείας \(ε\) για \(x=0\) έχουμε \(y=-4\). Επίσης για \(y=0\) είναι \(x=-4\). Άρα η \(ε\) τέμνει τον άξονα \(x'x\) στο σημείο \(Κ(-4,0)\) και τον \(y'y\) στο \(Λ(0,-4)\). Επομένως
\begin{align}(ΟΚΛ)&=\frac{1}{2}(ΟΚ)\cdot(ΟΛ)\\ &=\frac{1}{2}|x_Κ|\cdot|y_Λ|\\ &=\frac{1}{2}|-4|\cdot|-4|\\ &=\frac{1}{2}\cdot 4\cdot 4\\ &=\frac{1}{2}\cdot 16\\ &=8.\end{align}
Θέμα: 22073
ΘΕΜΑ 4
Σε χάρτη με καρτεσιανό σύστημα συντεταγμένων η θέση ενός λιμανιού προσδιορίζεται από το σημείο \(Λ(2,6)\) και η θέση ενός πλοίου με το σημείο \(Π(λ-1,2+λ)\), \(λ\in\mathbb{R}\).
α) i. Αν το πλοίο κινείται ευθύγραμμα, να βρείτε την εξίσωση της τροχιάς του.
(Μονάδες 7)
ii. Να εξετάσετε αν το πλοίο θα περάσει από το λιμάνι.
(Μονάδες 5)
β) Αν τελικά το πλοίο δεν περάσει από το λιμάνι, να βρείτε:
i. Ποια είναι η ελάχιστη απόσταση του πλοίου από το λιμάνι.
(Μονάδες 6)
ii. Το σημείο του καρτεσιανού επιπέδου που βρίσκεται το πλοίο όταν απέχει την ελάχιστη απόσταση από το λιμάνι.
(Μονάδες 7)
Απάντηση Θέματος: 22073
α) i. Για το σημείο \(Π(λ-1,2+λ)\) έχουμε:
$$\begin{cases}x_Π=λ-1\\y_Π=2+λ\end{cases}$$
Απαλείφοντας το \(λ\) από τις \(2\) εξισώσεις, έχουμε ότι \(y_Π=x_Π+3\). Επομένως η τροχιά του πλοίου είναι η ευθεία \((ε)\) με εξίσωση \(x-y+3=0\).
ii. Το πλοίο θα περάσει από το λιμάνι αν και μόνο αν οι συντεταγμένες του λιμανιού \(Λ(2,6)\) επαληθεύουν την εξίσωση της τροχιάς του, δηλαδή την εξίσωση \(x-y+3=0\). Για \(y=6\) και \(x=2\) έχουμε
$$2-6+3=-1\neq0.$$
Άρα το πλοίο δεν θα περάσει από το λιμάνι.
β)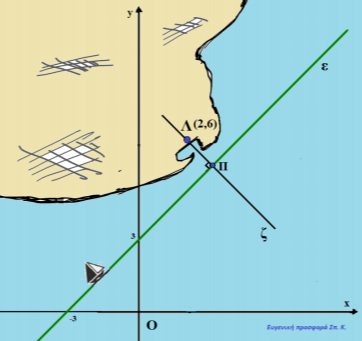
i. Η ελάχιστη απόσταση του πλοίου από το λιμάνι είναι το μήκος του κάθετου τμήματος \(ΛΠ\), με \(Π\) το σημείο τομής της ευθείας \((ε)\) με την ευθεία \((ζ)\) που είναι κάθετη στην \((ε)\) και διέρχεται από το \(Λ\). Υπολογίζεται με την απόσταση του σημείου \(Λ\) από την \((ε)\). Δηλαδή
\begin{align}d(Λ,ε)&=\frac{|2-6+3|}{\sqrt{1^2+(-1)^2}}\\ &=\frac{1}{\sqrt{2}}\\ &=\frac{\sqrt{2}}{2}.\end{align}
ii. Η ευθεία \((ζ)\) είναι κάθετη στην ευθεία \((ε)\), άρα \(λ_ζ\cdot λ_ε=-1\). Επειδή \(λ_ε=1\), έχουμε ότι \(λ_ζ=-1\) και η εξίσωση της \((ζ)\) είναι
\begin{align}&y-y_Λ=-(x-x_Λ)\\ \iff&y-6=-x+2\\ \iff&x+y=8.\end{align}
Η θέση του πλοίου είναι το κοινό σημείο των ευθειών \((ε)\) και \((ζ)\), που προσδιορίζεται από τη λύση του συστήματος:
\begin{align}&\begin{cases}x-y=-3\\x+y=8\end{cases}\\ \iff&\begin{cases}2x=5\\x+y=8\end{cases}\\ \iff&\begin{cases}x=\frac{5}{2}\\y=\frac{11}{2}\end{cases}\end{align}
Άρα όταν το πλοίο απέχει την ελάχιστη απόσταση από το λιμάνι, βρίσκεται στο σημείο \(\left(\dfrac{5}{2},\dfrac{11}{2}\right)\) του καρτεσιανού επιπέδου.
Θέμα: 22262
ΘΕΜΑ 4
Δίνεται τρίγωνο \(ΑΒΓ\) με κορυφές τα σημεία \(Α(-2,1)\), \(Β(1,5)\) και \(Γ(5,-1)\).
α) Να υπολογίσετε το εμβαδόν του τριγώνου \(ΑΒΓ\).
(Μονάδες 5)
β) Να βρείτε την εξίσωση της ευθείας \(ΒΓ\).
(Μονάδες 5)
γ) Να βρείτε την εξίσωση του ύψους του τριγώνου από την κορυφή \(Α\). Στη συνέχεια να βρείτε το σημείο \(Δ\) της ευθείας \(ΒΓ\) από το οποίο το \(Α\) απέχει την ελάχιστη απόσταση.
(Μονάδες 8)
δ) Να βρείτε το σύνολο των σημείων \(Μ\) του επιπέδου για τα οποία ισχύει \((ΜΑΒ)=\dfrac{1}{2}(ΑΒΓ)\).
(Μονάδες 7)
Απάντηση Θέματος: 22262
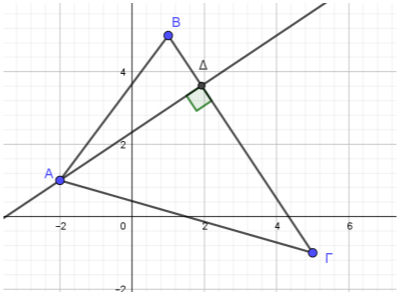
α) Είναι
\begin{align}\overrightarrow{AB}&=(x_B-x_A,y_B-y_A)\\ &=(1-(-2),5-1)\\ &=(3,4)\end{align}
και
\begin{align}\overrightarrow{ΑΓ}&=(x_Γ-x_A,y_Γ-y_A)\\ &=(5-(-2),-1-1)\\ &=(7,-2),\end{align}
οπότε
\begin{align}(ABΓ)&=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{ΑΓ})|\\ &=\frac{1}{2}|\!\begin{vmatrix}x_{AB}&y_{AB}\\x_{AΓ}&y_{AΓ}\end{vmatrix}|\\ &=\frac{1}{2}|\!\begin{vmatrix}3&4\\7&-2\end{vmatrix}|\\ &=\frac{1}{2}|3\cdot(-2)-4\cdot 7|\\ &=\frac{1}{2}|-6-28|\\ &=\frac{1}{2}|-34|\\ &=\frac{1}{2}\cdot 34\\ &=17.\end{align}
β) Η ευθεία \(ΒΓ\) έχει εξίσωση
\begin{align}&y-y_B=\frac{y_Γ-y_B}{x_Γ-x_B}(x-x_B)\\ \iff&y-5=\frac{-1-5}{5-1}(x-1)\\ \iff&y-5=\frac{-6}{4}(x-1)\\ \iff&y-5=-\frac{3}{2}(x-1)\\ \iff&2y-10=-3x+3\\ \iff&3x+2y-13=0.\end{align}
γ) Έστω \(υ_α\) το ύψος του τριγώνου από την κορυφή \(Α\). Είναι \(λ_{ΒΓ}=-\dfrac{A}{B}=-\dfrac{3}{2}\) και
\begin{align}&υ_α\perp ΒΓ\\ \iff&λ_{υ_α}\cdot λ_{ΒΓ}=-1\\ \iff&λ_{υ_α}=\frac{-1}{λ_{ΒΓ}}=\frac{-1}{-\frac{3}{2}}=\frac{2}{3}.\end{align}
Έτσι η εξίσωση του φορέα του \(υ_α\) είναι
\begin{align}&y-y_Α=λ_{υ_α}(x-x_Α)|\\ \iff&y-1=\frac{2}{3}(x-(-2))\\ \iff&3y-3=2x+4\\ \iff&2x-3y+7=0.\end{align}
Το σημείο της ευθείας \(ΒΓ\) που απέχει τη μικρότερη απόσταση από το \(Α\) είναι το ίχνος, \(Δ\), του ύψους από το \(Α\) στην ευθεία \(ΒΓ\). Από το σύστημα των \(ΒΓ\), θα έχουμε
$$\begin{cases}3x+2y=13\\2x-3y=-7\end{cases}$$
οπότε
\begin{align}D=\begin{vmatrix}3&2\\2&-3\end{vmatrix}=-9-4=-13,\\ D_x=\begin{vmatrix}13&2\\-7&-3\end{vmatrix}=-39+14=-25\end{align}
και
$$D_y=\begin{vmatrix}3&13\\2&-7\end{vmatrix}=-21-26=-47,$$
άρα η λύση του συστήματος είναι
$$x=\frac{D_x}{D}=\frac{-25}{-13}=\frac{25}{13}$$
και
$$y=\frac{D_y}{D}=\frac{-47}{-13}=\frac{47}{13}.$$
Επομένως, \(Δ\left(\dfrac{25}{13},\dfrac{47}{13}\right)\) είναι το ζητούμενο σημείο της ευθείας \(ΒΓ\).
δ) Έστω \(Μ(x, y)\) σημείο του επιπέδου ώστε \((ΜΑΒ)=\frac{1}{2}(ΑΒΓ)\), η οποία λόγω του ερωτήματος (α) γράφεται \((ΜΑΒ)=\frac{17}{2}\). Είναι
\begin{align}\overrightarrow{AM}&=(x_M-x_A,y_M-y_A)\\ &=(x-(-2),y-1)\\ &=(x+2,y-1),\end{align}
άρα
\begin{align}(MAB)&=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AM})|\\ &=\frac{1}{2}|\!\begin{vmatrix}3&4\\x+2&y-1\end{vmatrix}|\\ &=\frac{1}{2}|3(y-1)-4(x+2)|\\ &=\frac{1}{2}|3y-3-4x-8|\\ &=\frac{1}{2}|3y-4x-11|\end{align}
οπότε
\begin{align}&(MAB)=\frac{17}{2}\\ \iff&\frac{1}{2}|3y-4x-11|=\frac{17}{2}\\ \iff&|3y-4x-11|=17\\ \iff&3y-4x-11=\pm 17\\ \iff&4x-3y-6=0\text{ ή }4x-3y+28=0.\end{align}
Άρα το σημείο \(Μ\) ανήκει σε μια εκ των ευθείων \(ε_1:4x-3y-6=0\) και \(ε_2:4x-3y+28=0\).
Θέμα: 22265
ΘΕΜΑ 4
Στο καρτεσιανό επίπεδο δίνονται τα σημεία \(Α(1,-1)\), \(Β(2,2)\) και \(Γ(μ-1,3μ-2)\), \(μ\in\mathbb{R}\).
α) Να αποδείξετε ότι καθώς το \(μ\) διατρέχει το \(\mathbb{R}\), το σημείο \(Γ\) κινείται στην ευθεία \(ε: y=3x+1\).
(Μονάδες 6)
β) Να αποδείξετε ότι καθώς το \(μ\) διατρέχει το \(\mathbb{R}\), τα σημεία \(Α\), \(Β\), \(Γ\) είναι κορυφές τριγώνου.
(Μονάδες 6)
γ) Να αποδείξετε ότι το εμβαδόν του τριγώνου \(ΑΒΓ\) είναι σταθερό.
(Μονάδες 5)
δ) Να βρείτε τις εξισώσεις των ευθειών που διέρχονται από το σημείο \(Β\) και από τις οποίες το σημείο \(Α\) απέχει απόσταση ίση με \(1\).
(Μονάδες 8)
Απάντηση Θέματος: 22265
α) Καθώς το \(μ\) διατρέχει το \(\mathbb{R}\), είναι \(Γ(μ-1,3μ-2)\), οπότε αν \(Γ(x, y)\) τότε
\begin{align}&\begin{cases}x=μ-1\\y=3μ-2\\μ\in\mathbb{R}\end{cases}\\ \iff&\begin{cases}μ=x+1\\y=3(x+1)-2\\μ\in\mathbb{R}\end{cases}\\ \iff&\begin{cases}y=3x+1\\μ=x+1\\μ\in\mathbb{R}\end{cases}\end{align}
επομένως το σημείο \(Γ\) κινείται στην ευθεία \(ε:y=3x+1\).
β) Είναι
\begin{align}λ_{ΑΒ}&=\frac{y_Β-y_Α}{x_Β-x_Α}\\ &=\frac{2-(-1)}{2-1}\\ &=3\\ &=λ_ε,\end{align}
άρα \(ΑΒ//ε\). Επιπλέον, για \(x=1\) και \(y=-1\) από την εξίσωση της \((ε)\) παίρνουμε \(-1=3\cdot1+1\), που δεν ισχύει. Άρα το σημείο \(Α\) δεν ανήκει στην ευθεία \(ε\), αφού οι συντεταγμένες του δεν ικανοποιούν την εξίσωσή της. Οπότε τα σημεία \(Α\), \(Β\), \(Γ\) δεν είναι συνευθειακά. Επομένως, καθώς το μ διατρέχει το \(\mathbb{R}\), τα σημεία \(Α\), \(Β\), \(Γ\) είναι κορυφές τριγώνου.
γ) Είναι
\begin{align}\overrightarrow{AB}&=(x_B-x_A,y_B-y_A)\\ &=(2-1,2-(-1))\\ &=(1,3)\end{align}
και
\begin{align}\overrightarrow{ΑΓ}&=(x_Γ-x_A,y_Γ-y_A)\\ &=(μ-1-1,3μ-2-(-1))\\ &=(μ-2,3μ-1),\end{align}
οπότε
\begin{align}(ABΓ)&=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{ΑΓ})|\\ &=\frac{1}{2}|\!\begin{vmatrix}1&3\\μ-2&3μ-1\end{vmatrix}|\\ &=\frac{1}{2}|1(3μ-1)-3(μ-2)|\\ &=\frac{1}{2}|3μ-1-3μ+6|\\ &=\frac{1}{2}|5|\\ &=\frac{5}{2},\end{align}
σταθερό για κάθε \(μ\in\mathbb{R}\).
Εναλλακτικά: Λόγω των ερωτημάτων (α) και (β), το ύψος του τριγώνου \(ΑΒΓ\) από την κορυφή του \(Γ\) στην \(ΑΒ\), έχει σταθερό μήκος, ίσο με την απόσταση των παραλλήλων ευθειών \((ε)\) και \(ΑΒ\). Επίσης το μήκος του \(ΑΒ\) είναι σταθερό, οπότε το εμβαδό του τριγώνου είναι σταθερό.
δ) Από το σημείο \(Β(2,2)\) διέρχονται οι ευθείες \(δ':x=2\) και \((δ)\) με εξίσωση
\begin{align}&y-y_Β=λ(x-x_Β)\\ \iff&y-2=λ(x-2)\\ \iff&λx-y+2-2λ=0.\end{align}
Είναι
$$d(A,δ')=|2-x_Α|=|2-1|= 1,$$
οπότε η ευθεία \(δ':x=2\) αποτελεί μια λύση στο πρόβλημα. Θα αναζητήσουμε αν στην οικογένεια ευθειών \(δ\) υπάρχει και άλλη ευθεία που να αποτελεί λύση στο πρόβλημα. Είναι
\begin{align}d(A,δ)&=\frac{|λ\cdot1-1\cdot(-1)+2-2λ|}{\sqrt{λ^2+(-1)^2}}\\ &=\frac{|λ+1+2-2λ|}{\sqrt{λ^2+1}}\\ &=\frac{|3-λ|}{\sqrt{λ^2+1}}.\end{align}
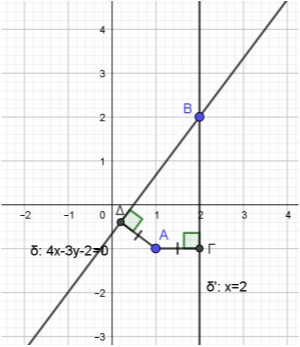
Θέλουμε
\begin{align}&d(A,δ)=1\\ \iff&\frac{|3-λ|}{\sqrt{λ^2+1}}=1\\ \iff&|3-λ|=\sqrt{λ^2+1}\\ \iff&|3-λ|^2=\sqrt{λ^2+1}^2\\ \iff&(3-λ)^2=λ^2+1\\ \iff&9-6λ+λ^2=λ^2+1\\ \iff&6λ=8\\ \iff&λ=\frac{8}{6}=\frac{4}{3}.\end{align}
Για \(λ=\dfrac{4}{3}\), η ευθεία \((δ)\) με εξίσωση
$$\frac{4}{3}x-y+2-2\frac{4}{3}=0\iff 4x-3y-2=0$$
αποτελεί μία ακόμη λύση στο πρόβλημα.
Θέμα: 22266
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$(2λ+1)x-(λ-2)y+λ-7=0\quad(Ε), \text{ με }λ\in\mathbb{R}$$
και η ευθεία \((ζ)\) με εξίσωση \(6x-8y+3=0\).
α) Να αποδείξετε ότι για κάθε \(λ\in\mathbb{R}\) η εξίσωση \((Ε)\) παριστάνει ευθεία.
(Μονάδες 6)
β) Να αποδείξετε ότι όλες οι ευθείες που ορίζονται από την εξίσωση \((Ε)\), για τα διάφορα \(λ\in\mathbb{R}\), διέρχονται από το ίδιο σημείο, του οποίου να βρείτε τις συντεταγμένες.
(Μονάδες 7)
γ) Να βρείτε την τιμή του \(λ\in\mathbb{R}\), ώστε ευθεία \((ε)\) που ορίζεται από την εξίσωση \((Ε)\) να είναι παράλληλη στη ευθεία \((ζ)\). Ποια είναι η εξίσωση της \((ε)\);
(Μονάδες 7)
δ) Να βρείτε την απόσταση του σημείου \(Μ(1,3)\) από την ευθεία \((ζ)\).
(Μονάδες 5)
Απάντηση Θέματος: 22266
α) Έχουμε την εξίσωση
$$(2λ+1)x-(λ-2)y+λ-7=0\quad (Ε)$$
με \(λ\in\mathbb{R}\) που είναι της μορφής \(Αx+Βy+Γ=0\), με \(Α=2λ+1\) και \(Β= λ-2\). Οπότε
\begin{align}&\begin{cases}Α=0\\Β=0\end{cases}\\ \iff&\begin{cases}2λ+1=0\\λ-2=0\end{cases}\\ \iff&\begin{cases}λ=-\frac{1}{2}\\λ=2\end{cases}\end{align}
και άρα για κάθε \(λ\in\mathbb{R}\) είναι \(Α\neq0\) ή \(Β\neq0\), επομένως η εξίσωση \((Ε)\) παριστάνει ευθεία.
β) Η εξίσωση \((Ε)\) γράφεται
\begin{align}&2λx+x-λy+2y+λ-7=0\\ \iff&(2x-y+1)λ+(x+2y-7)=0.\end{align}
Για να αληθεύει για κάθε \(λ\) η παραπάνω εξίσωση πρέπει και αρκεί:
\begin{align}&\begin{cases}2x-y+1=0\\x+2y-7=0\end{cases}\\ \iff&\begin{cases}y=2x+1\\x+2(2x+1)-7=0\end{cases}\\ \iff&\begin{cases}y=2x+1\\x+4x+2-7=0\end{cases}\\ \iff&\begin{cases}x=1\\y=3\end{cases}\end{align}
Επομένως, όλες οι ευθείες που ορίζονται από την εξίσωση \((Ε)\) διέρχονται από το σημείο \(Μ(1,3)\).
γ) Η ευθεία \((ζ)\) είναι παράλληλη στο διάνυσμα \(\vec{δ}_1=(Β,-Α)=(-8,-6)\). Οι ευθείες της οικογένειας ευθειών \((Ε)\) είναι παράλληλες στο διάνυσμα \(\vec{δ}_2=(Β,-Α)=(-λ+2,-2λ-1)\). Οπότε
\begin{align}&\vec{δ}_1\parallel \vec{δ}_2\\ \iff&\det(\vec{δ}_1,\vec{δ}_2)=0\\ \iff&\begin{vmatrix}-8&-6\\-λ+2&-2λ-1\end{vmatrix}=0\\ \iff&16λ+8-6λ+12=0\\ \iff&10λ=-20\\ \iff&λ=-2.\end{align}
Για \(λ=-2\) από την εξίσωση \((Ε)\) παίρνουμε \(-3x+4y-9=0\). Άρα \(ε:-3x+4y-9=0\) είναι η ζητούμενη ευθεία.
δ) Είναι \((ζ): 6x-8y+3=0\), οπότε
\begin{align}d(M,ζ)&=\frac{|6\cdot1-8\cdot3+3|}{\sqrt{6^2+(-8)^2}}\\ &=\frac{|15|}{\sqrt{100}}\\ &=\frac{15}{10}\\ &=\frac{3}{2}.\end{align}
