Μάθημα : Β΄ΛΥΚΕΙΟΥ - ΜΑΘΗΜΑΤΙΚΑ ΠΡ. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
Κωδικός : G217111
G217111 - ΧΡΗΣΤΟΣ ΤΡΙΑΝΤΗΣ
Ενότητες μαθήματος - Κεφάλαιο 3ο: - ΚΩΝΙΚΕΣ ΤΟΜΕΣ- Λυμένα θέματα από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
Κεφάλαιο 3ο: - ΚΩΝΙΚΕΣ ΤΟΜΕΣ- Λυμένα θέματα από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
31 ΚΥΚΛΟΣ
Θέμα: 14953
ΘΕΜΑ 2
Θεωρούμε τρίγωνο \(ΑΒΓ\) με \(Α(-2,5),\ Β(7,8),\ Γ(1,-4).\)
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}.\)
(Μονάδες 10)
β) Να υπολογίσετε το εσωτερικό γινόμενο \(\overrightarrow{AB} \cdot \overrightarrow{AΓ}.\)
(Μονάδες 10)
γ) Να βρείτε, σε μοίρες, την κυρτή γωνία \(B\hat{A}Γ\).
(Μονάδες 5)
Απάντηση Θέματος: 14953
α) Βρίσκουμε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}\):
$$\overrightarrow{AB}=(7 –(–2),8 – 5)=(9,3)$$ $$\overrightarrow{AΓ}=(1 –(–2),– 4 – 5)=(3,–9)$$
β) Σύμφωνα με την αναλυτική έκφραση του εσωτερικού γινομένου, θα έχουμε:
$$\overrightarrow{AB} \cdot \overrightarrow{AΓ} =9 \cdot 3+3\cdot (− 9)=27 − 27=0.$$
γ) Αν \(θ=(\widehat{\overrightarrow{AB},\overrightarrow{AΓ}})=Β\hat{A}Γ\), γνωρίζουμε ότι
$$\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}=|\overrightarrow{AB}||\overrightarrow{ΑΓ}|συνθ,$$
άρα \(συνθ=0\). Αλλά \(0\leq θ\leq π\), έτσι \(θ=90^ο\).
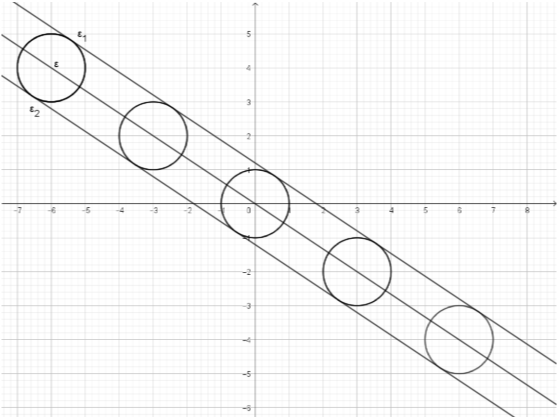
Θέμα: 14954
ΘΕΜΑ 4
Θεωρούμε τις εξισώσεις
$$ε_1: μx-y-μ=0$$
και
$$ε_2: (μ+1)x+(μ-1)y-μ+1=0$$
με \(μ\in\mathbb{R}\).
α) Να αποδείξετε ότι οι \((ε_1)\) και \((ε_2)\) παριστάνουν εξισώσεις ευθειών για κάθε τιμή της παραμέτρου \(μ\).
(Μονάδες 6)
β) Να αποδείξτε ότι η οξεία γωνία των ευθειών \((ε_1)\) και \((ε_2)\) είναι \(45^ο\) για κάθε τιμή της παραμέτρου \(μ\).
(Μονάδες 10)
γ) Να αποδείξετε ότι τα σημεία τομής των ευθειών \((ε_1)\) και \((ε_2)\) ανήκουν στον κύκλο με κέντρο την αρχή των αξόνων και ακτίνα \(1\).
(Μονάδες 9)
Απάντηση Θέματος: 14954
α) Κάθε μια από τις εξισώσεις \((ε_1)\) και \((ε_2)\) είναι στη μορφή \(Αx+By+Γ=0\), η εξίσωση που γνωρίζουμεότι παριστάνει ευθεία όταν \(|Α|+|Β|>0\), δηλαδή όταν οι αριθμοί \(Α\) και \(Β\) δεν είναι ταυτόχρονα μηδέν.
Παρατηρούμε ότι στην \((ε_1)\) είναι \(Β=-1\neq 0\), ενώ στην \((ε_2)\) είναι \(A=μ+1, Β=μ-1\) και \(Α=0\) για \(μ=-1, Β=0\) για \(μ=1\). Έτσι, δεν υπάρχει τιμή της παραμέτρου \(μ\) η οποία να μηδενίζει ταυτόχρονα τους συντελεστές \(Α\) και \(Β\).
β) Γνωρίζουμε ότι η ευθεία με εξίσωση \(Ax+By+Γ=0\) είναι παράλληλη προς το διάνυσμα \(\vec{δ}=(-B,A)\). Έτσι, θα είναι \(\vec{δ_1}=(1,μ)\) παράλληλο στην \((ε_1)\) και \(\vec{δ_2}=(1-μ,1+μ)\) παράλληλο στην \((ε_2)\). Οπότε η οξεία γωνία \(θ\) των \((ε_1)\) και \((ε_2)\) θα είναι ίση ή παραπληρωματική της οξείας γωνίας \(φ\) των διανυσμάτων \(\vec{δ_1}\) και \(\vec{δ_2}\). Είναι \(συνφ=\dfrac{\vec{δ_1}\cdot\vec{δ_2}}{|\vec{δ_1}|\cdot|\vec{δ_2}|}\). Αλλά
\begin{align}\vec{δ_1}\cdot\vec{δ_2}&=1\cdot (1-μ)+μ\cdot (1+μ)\\ &=1-μ+μ+μ^2\\ &=1+μ^2\end{align}
και
\begin{align}|\vec{δ_2}|&=\sqrt{(1-μ)^2+(1+μ)^2}\\ &=\sqrt{1-2μ+μ^2+1+2μ+μ^2}\\ &=\sqrt{2+2μ^2}\\ &=\sqrt{2(1+μ^2)}\\ &=\sqrt{2}\sqrt{1+μ^2}\\ &=\sqrt{2}\cdot |\vec{δ_1}|.\end{align}
Έτσι,
\begin{align}συνφ&=\frac{1+μ^2}{|\vec{δ_1}\cdot\sqrt{2}\cdot |\vec{δ_2}|}\\ &=\frac{1+μ^2}{\sqrt{2}|\vec{δ_1}|^2}\\ &=\frac{1+μ^2}{\sqrt{2}(1+μ^2)}\\ &=\frac{\sqrt{2}}{2}.\end{align}
Ώστε \(θ=45^o\).
γ) Για να βρούμε πού τέμνονται οι ευθείες \((ε_1)\) και \((ε_2)\) αρκεί να λύσουμε το σύστημα των εξισώσεων \((ε_1)\) και \((ε_2)\). Ένας τρόπος είναι με τη μέθοδο της αντικατάστασης. Από την \((ε_1)\) παίρνουμε \(y=μx-μ\), οπότε αντικαθιστώντας στην \((ε_2)\) παίρνουμε
\begin{align}&(μ+1)x+(μ-1)(μx-μ)-μ+1=0\\ \iff&(μ+1)x+μ(μ-1)x-μ(μ-1)-μ+1=0\\ \iff&(μ+1+μ^2-μ)x-μ^2+μ-μ+1=0\\ \iff&x=\frac{μ^2-1}{μ^2+1}.\end{align}
Τότε
\begin{align}y&=μ\frac{μ^2-1}{μ^2+1}-μ\\ &=\frac{μ^3-μ-μ^3-μ}{μ^2+1}\\ &=\frac{-2μ}{μ^2+1}.\end{align}
Έτσι τα σημεία τομής των \((ε_1)\) και \((ε_2)\) είναι τα \(Σ_μ\left(\dfrac{μ^2-1}{μ^2+1},\dfrac{-2μ}{μ^2+1}\right)\) για κάθε τιμή της παραμέτρου \(μ\).
Ο ζητούμενος κύκλος έχει εξίσωση \(x^2+y^2=1\). Αρκεί λοιπόν να δείξουμε ότι οι συντεταγμένες των σημείων \(Σ_μ\) επαληθεύουν την εξίσωση αυτή. Πράγματι,
\begin{align}&\phantom{{}={}}\left(\frac{μ^2-1}{μ^2+1}\right)^2+\left(\frac{-2μ}{μ^2+1}\right)^2\\ &=\frac{μ^4-2μ^2+1+4μ^2}{(1+μ^2)^2}\\ &=\frac{μ^4+2μ^2+1}{(μ^2+1)^2}\\ &=1.\end{align}
Τα παραπάνω αποτυπώνονται στο παρακάτω σχήμα.
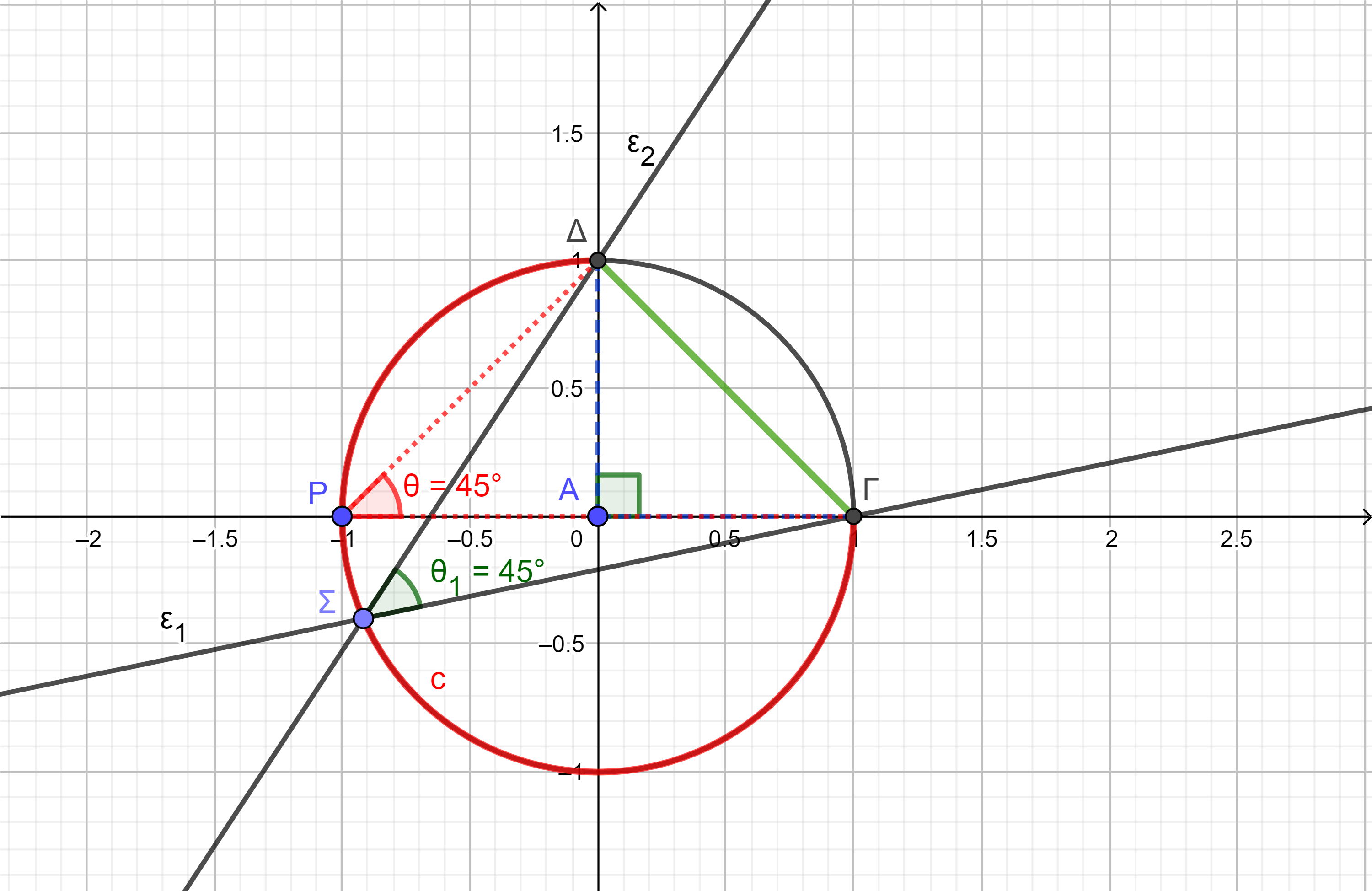
Σχόλιο :
Εύκολα αποδεικνύεται ότι οι ευθείες της μορφής \((ε_1)\) διέρχονται από το σταθερό σημείο \(Γ(1,0)\) ενώ οι ευθείες της μορφής \((ε_2)\) διέρχονται από το σταθερό σημείο \(Δ(0,1)\) για κάθε τιμή της παραμέτρου \(μ\in\Bbb{R}\). Επομένως, το τμήμα \(ΓΔ\) είναι σταθερό και τα σημεία τομής \(Σ\) των ευθειών \((ε_1),(ε_2)\), που σχηματίζουν οξεία γωνία \(45^0\) ή αμβλεία γωνία \(135^0\) είναι τα σημεία του κύκλου. Έτσι η γωνία \(Δ\hat{Σ}Γ\) είναι εγγεγραμμένη που βαίνει στο τόξο \(\overset{\frown}{ΓΔ}\) και είναι \(45^0\) ή \(135^0\) αντίστοιχα.
Θέμα: 14984
ΘΕΜΑ 4
Θεωρούμε τα σημεία \(A(-2,-3)\) και \(B(7,9)\). Έστω \(S\) το σύνολο των σημείων \(Μ\) που είναι κορυφές των τριγώνων \(ΑΜΒ\) ώστε \((AMB)=12\) τ.μ.
α) Να αποδείξτε ότι το \(S\) αποτελείται από τα σημεία των παραλλήλων ευθειών \(ε_1:4x-3y-9=0\) και \(ε_2:4x-3y+7=0\).
(Μονάδες 9)
β) Να αποδείξετε ότι η ευθεία \(ΑΒ\) είναι η μεσοπαράλληλη των \((ε_1)\) και \((ε_2)\).
(Μονάδες 9)
γ) Θεωρούμε ένα σημείο \(Μ_1\) στην \((ε_1)\) και ένα σημείο \(Μ_2\) στην \((ε_2)\) ώστε να σχηματίζεται το τετράπλευρο \(ΑΜ_1ΒΜ_2\). Πόσο είναι το εμβαδόν του; Πόσα τετράπλευρα \(ΑΧΒY\) υπάρχουν, αν το \(Χ\) πρέπει να είναι σημείο της \((ε_1)\) και το \(Y\) σημείο της \((ε_2)\), που έχουν το ίδιο εμβαδό με το \(ΑΜ_1ΒΜ_2\); Εξηγήστε.
(Μονάδες 7)
Απάντηση Θέματος: 14984
α) Πρέπει να ισχύει
\begin{align}&\frac{1}{2}|\det(\overrightarrow{AM},\overrightarrow{AB})|=12\\ \iff&|\begin{vmatrix}x+2&y+3\\9&12\end{vmatrix}|=24.\end{align}
Αναπτύσσοντας την ορίζουσα παίρνουμε
\begin{align}&|12(x+2)-9(y+3)|=24\\ \iff&3|4(x+2)-3(y+3)|=24\\ \iff&|4x+8-3y-9|=8\\ \iff&|4x-3y-1|=8.\end{align}
Τελικά έχουμε \(4x-3y-1=8\) ή \(4x-3y-1=-8\), δηλαδή \(4x-3y=9\) ή \(4x-3y =-7\) οι οποίες είναι εξισώσεις των ευθειών \((ε_1)\) και \((ε_2)\). Οι ευθείες είναι παράλληλες αφού έχουν κοινό συντελεστή διεύθυνσης \(λ=\dfrac{4}{3}\).
β) Παρατηρούμε ότι
$$λ_{ΑΒ}=\frac{y_B-y_A}{x_B-x_A}=\frac{9-(-3)}{7-(-2)}=\frac{4}{3},$$
άρα η ευθεία \(ΑΒ\) είναι παράλληλη στις \((ε_1)\) και \((ε_2)\). Επομένως αρκεί να αποδείξουμε ότι ένα οποιοδήποτε σημείο της \(ΑΒ\) ισαπέχει από τις \((ε_1)\) και \((ε_2)\). Για ευκολία βρίσκουμε το μέσο του \(ΑΒ\) που είναι το σημείο \(Κ\left(\dfrac{-2+7}{2},\dfrac{-3+9}{2}\right)\) δηλαδή το \(K\left(\dfrac{5}{2},3\right)\). Τώρα
$$d(K,ε_1)=\frac{|4\cdot\frac{5}{2}-3\cdot 3-9|}{\sqrt{4^2+(-3)^2}}=\frac{8}{5}$$
και
$$d(K,ε_2)=\frac{|4\cdot\frac{5}{2}-3\cdot 3+7|}{\sqrt{4^2+(-3)^2}}=\frac{8}{5}.$$
γ) Με βάση το παρακάτω σχήμα, διαπιστώνουμε ότι οποιοδήποτε σημείο \(Μ_1\) της \((ε_1)\) σχηματίζει με το σταθερό ευθύγραμμο τμήμα \(ΑΒ\) τρίγωνο σταθερού εμβαδού, αφού το ύψος \(h\) του τριγώνου \(ΑΜΒ\) που αντιστοιχεί στην \(ΑΒ\) είναι σταθερό και ίσο με το μισό της απόστασης των \((ε_1)\) και \((ε_2)\), οπότε
$$(ΑM_1B)=\frac{1}{2}\cdot AB\cdot h = \frac{1}{2}\cdot15\cdot\frac{8}{5}=12,$$
αφού
$$AB=\sqrt{(7+2)^2+(9+3)^2}=\sqrt{225}=15.$$
Ανάλογα, \((AM_2B)=12\), έτσι \((AM_1BM_2)=24\). Ώστε \((AXBY)=24\) για οποιαδήποτε σημεία \(Χ,Y\) των \((ε_1)\) και \((ε_2)\) αντίστοιχα, αρκεί να σχηματίζεται τετράπλευρο (να μην είναι για παράδειγμα τα σημεία \(Μ_1, Β, Μ_2\) συνευθειακά). Άρα υπάρχουν άπειρα τετράπλευρα \(ΑXBY\) με σταθερό εμβαδόν \(24\).
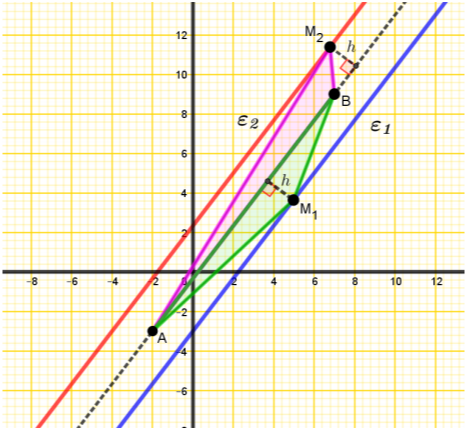
Θέμα: 15028
ΘΕΜΑ 2
Έστω κύκλος \(C\) με κέντρο \(K(1,2)\) και ακτίνα \(ρ=2\) και ευθεία \((ε)\) με εξίσωση \(3x+4y-1=0\).
α) Να γράψετε την εξίσωση του κύκλου \(C.\)
(Μονάδες 8)
β) Να δείξετε ότι η απόσταση του κέντρου \(K(1, 2)\) από την ευθεία \((ε)\) είναι ίση με \(2.\)
(Μονάδες 9)
γ) Να δείξετε ότι η ευθεία \((ε)\) εφάπτεται στον κύκλο \(C.\)
(Μονάδες 8)
Απάντηση Θέματος: 15028
α) Είναι \(C:\ (x-1)^2+(y-2)^2=4.\)
β) Είναι \(d(K,ε)=\dfrac{|3\cdot 1+4\cdot 2-1|}{\sqrt{3^2+4^2}}=2\)
γ) Αφού \(d(K,ε)=2=ρ\) η ευθεία \((ε)\) εφάπτεται στον κύκλο \(C.\)
Θέμα: 15030
ΘΕΜΑ 4
Δίνεται ο κύκλος
$$C:(x-2)^2+(y+3)^2=5$$
και η ευθεία
$$ε:2x+y+5=0.$$
α) Να βρείτε το κέντρο και την ακτίνα του κύκλου \(C\).
(Μονάδες 6)
β) Να δείξετε ότι ο κύκλος \(C\) και η ευθεία \((ε)\) δεν έχουν κοινά σημεία.
(Μονάδες 6)
γ) Να δείξετε ότι υπάρχουν δύο ευθείες \((η_1),\ (η_2)\) που είναι παράλληλες στην ευθεία \((ε)\) και εφάπτονται του κύκλου \(C\) και να βρείτε τι εξισώσεις τους.
(Μονάδες 7)
δ) Να βρείτε τη μεσοπαράλληλη των ευθειών \((η_1),\ (η_2)\).
(Μονάδες 6)
Απάντηση Θέματος: 15030
ΛΥΣΗ
α) Ο κύκλος \(C\) έχει κέντρο το \(Κ(2,-3)\) και ακτίνα \(ρ=\sqrt{5}\).
β) Είναι
\begin{align}d(Κ,ε)&=\frac{|2\cdot 2+1\cdot(-3)+5|}{\sqrt{2^2+1^2}}\\ &=\frac{|6|}{\sqrt{5}}=\frac{6\sqrt{5}}{5}> \sqrt{5}=ρ\end{align}
και αφού \(d(Κ,ε) > ρ\) ο κύκλος \(C\) και η ευθεία \((ε)\) δεν έχουν κοινά σημεία.
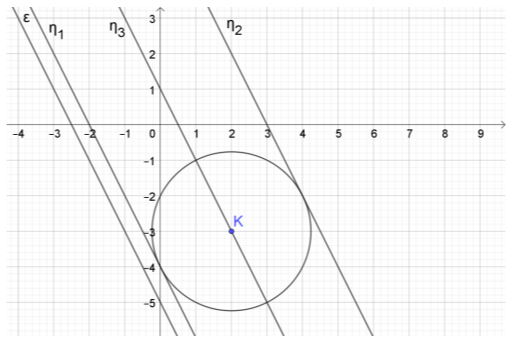
γ) Κάθε ευθεία \((η)\) παράλληλη στην \((ε)\) έχει τον ίδιο συντελεστή διεύθυνσης με την ευθεία \((ε)\), δηλαδή \(λ_η=-2\). Έτσι
$$η:y=-2x+β\iff 2x+y-β=0.$$
Για να εφάπτεται η ευθεία \((η)\) στον κύκλο πρέπει και αρκεί να απέχει από το κέντρο του απόσταση ίση με την ακτίνα του, δηλαδή
\begin{align}&d(Κ,η)=ρ\\ \iff&\frac{|2\cdot2+1\cdot(-3)-β|}{\sqrt{2^2+1^2}}=\sqrt{5}\\ \iff&\frac{|1-β|}{\sqrt{5}}=\sqrt{5}\\ \iff&|1-β|=5\\ \iff&1-β=5\text{ ή }1-β=-5\\ \iff&β=-4\text{ ή }β=6.\end{align}
Συνεπώς έχουμε δύο εφαπτομένες, τις
$$η_1:2x+y+4=0$$
και
$$η_2:2x+y-6=0$$
όπως φαίνεται στο παρακάτω σχήμα.
δ) Είναι \(d(Κ,η_1)=d(Κ,η_2)=ρ\), δηλαδή το \(Κ(2, -3)\) ισαπέχει από τις ευθείες \((η_1),\ (η_2)\), οπότε ανήκει στη μεσοπαράλληλή τους. Η ζητούμενη μεσοπαράλληλη \((η_3)\) ως παράλληλη στις \((η_1),\ (η_2)\) θα έχει συντελεστή διεύθυνσης \(λ_{η_3}=-2\). Τελικά η ζητούμενη μεσοπαράλληλη είναι η
$$η_3:y+3=-2(x-2)\iff y=-2x+1.$$
Θέμα: 15042
ΘΕΜΑ 4
Δίνεται τρίγωνο \(ΑΒΓ\) και σημείο του επιπέδου \(Μ\), τέτοιο ώστε
$$\overrightarrow{AB}-2\overrightarrow{AM}+\overrightarrow{ΑΓ}=\vec{0}.$$
α) Να αποδείξετε ότι τα σημεία \(Β\), \(Γ\), \(Μ\) είναι συνευθειακά.
(Μονάδες 8)
β) Να αποδείξετε ότι το \(Μ\) είναι το μέσο του \(ΒΓ\).
(Μονάδες 2)
γ) Έστω πραγματικοί αριθμοί \(κ\), \(λ\) τέτοιοι ώστε \(\overrightarrow{AB}\cdot\overrightarrow{AΓ}=κ\) και \(\overrightarrow{AM}\cdot\overrightarrow{ΒΓ}=λ\). Αν επιπλέον είναι γνωστό ότι για τα μη παράλληλα διανύσματα \(\overrightarrow{ΑΓ}\), \(\overrightarrow{AB}\) ισχύει ότι \(κ\overrightarrow{ΑΓ}=λ\overrightarrow{AB}\), τότε:
i. Να αποδείξετε ότι \(κ=λ=0\).
(Μονάδες 7)
ii. Να αποδείξετε ότι το τρίγωνο \(ΑΒΓ\) είναι ορθογώνιο και ισοσκελές. Να προσδιορίσετε την ορθή γωνία και τις πλευρές που είναι ίσες.
(Μονάδες 8)
Απάντηση Θέματος: 15042
α) Αρκεί να αποδειχθεί ότι υπάρχει \(μ\in\mathbb{R}\) έτσι ώστε \(\overrightarrow{BΓ}=μ\overrightarrow{BM}\). Πράγματι, θεωρώντας το \(Β\) ως σημείο αναφοράς, είναι:
\begin{align}&\overrightarrow{AB}-2\overrightarrow{AM}+\overrightarrow{ΑΓ}=\vec{0}\\ \iff&\overrightarrow{AB}-2(\overrightarrow{BM}-\overrightarrow{BA})+(\overrightarrow{BΓ}-\overrightarrow{BA})=\vec{0}\\ \iff&\overrightarrow{AB}+2\overrightarrow{BA}+\overrightarrow{BΓ}-\overrightarrow{BA}=2\overrightarrow{BM}\\ \iff&\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{BΓ}=2\overrightarrow{BM}\\ \iff&\overrightarrow{ΒΓ}=2\overrightarrow{BM}.\end{align}
β) Το \(Μ\) είναι το μέσο του τμήματος \(ΒΓ\), διότι
\begin{align}&\overrightarrow{BΓ}=2\overrightarrow{BM}\\ \iff&\overrightarrow{BΓ}-\overrightarrow{BM}=\overrightarrow{BM}\\ \iff&\overrightarrow{ΜΓ}=\overrightarrow{BM}.\end{align}
γ) i. Επειδή τα σημεία \(A\), \(Β\), \(Γ\) ως κορυφές τριγώνου δεν είναι συνευθειακά, έχουμε ότι τα μη μηδενικά διανύσματα \(\overrightarrow{AB}\), \(\overrightarrow{AΓ}\) δεν είναι παράλληλα. Είναι \(κ\overrightarrow{AΓ}=λ\overrightarrow{AB}\). Αν \(κ\neq 0\), τότε
\begin{align}&κ\overrightarrow{AΓ}=λ\overrightarrow{AB}\\ \implies&\overrightarrow{AΓ}=\frac{λ}{κ}\overrightarrow{AB}\\ \implies&\overrightarrow{ΑΓ}\parallel \overrightarrow{AB}.\end{align}
Αν \(λ\neq 0\), τότε
\begin{align}&κ\overrightarrow{ΑΓ}=λ\overrightarrow{ΑΒ}\\ \implies&\overrightarrow{AB}=\frac{κ}{λ}\overrightarrow{AΓ}\\ \implies&\overrightarrow{AΓ}\parallel \overrightarrow{AB}.\end{align}
Επομένως πρέπει \(κ=λ=0\).
ii) Είναι:
$$\begin{cases}\overrightarrow{ΑΒ}\cdot\overrightarrow{AΓ}=0\\\overrightarrow{AM}\cdot\overrightarrow{BΓ}=0\end{cases}
Αφού \(\overrightarrow{AB}\cdot\overrightarrow{AΓ}=0\) έπεται ότι τα διανύσματα \(\overrightarrow{AB}\), \(\overrightarrow{AΓ}\) είναι κάθετα. Επομένως, το τρίγωνο είναι ορθογώνιο με \(\hat{A}=90^o\). Αφού \(\overrightarrow{AM}\cdot\overrightarrow{BΓ}\), έπεται ότι η διάμεσος \(ΑΜ\) του ορθογώνιου τριγώνου είναι κάθετη στην πλευρά \(ΒΓ\), δηλαδή είναι και ύψος. Ως εκ τούτου το τρίγωνο είναι και ισοσκελές με \(AB=AΓ\).
Θέμα: 15080
ΘΕΜΑ 4
Δίνονται οι εξισώσεις
$$C_1:x^2+y^2-2x-8=0\quad(1)$$
και
$$C_2:x^2+y^2-6x+8=0\quad(2)$$
α) Να δείξετε ότι οι \((1)\) και \((2)\) είναι εξισώσεις κύκλων, με κέντρα \(K(1,0)\), \(Λ(3,0)\) και ακτίνες \(ρ_1=3\), \(ρ_2=1\), αντίστοιχα.
(Μονάδες 6)
β) i. Να βρείτε το μήκος της διακέντρου \(ΚΛ\).
(Μονάδες 5)
ii. Να δείξετε ότι ο κύκλος \(C_2\) εφάπτεται εσωτερικά του κύκλου \(C_1\).
(Μονάδες 5)
γ) Να βρείτε τις εξισώσεις των ακτίνων του κύκλου \(C_1\) που εφάπτονται στον κύκλο \(C_2\).
(Μονάδες 9)
Απάντηση Θέματος: 15080
α) Η εξίσωση της μορφής \(x^2+y^2+Ax+By+Γ=0\) παριστάνει κύκλο με κέντρο \(Κ\left(-\dfrac{A}{2},-\dfrac{B}{2}\right)\) και ακτίνα \(ρ=\dfrac{\sqrt{A^2+B^2-4Γ}}{2}\) αν και μόνο αν \(Α^2+Β^2-4Γ > 0\). Για την εξίσωση \((1)\) έχουμε
$$A^2+B^2-4Γ=4-4(-8)=36>0,$$
δηλαδή παριστάνει κύκλο με κέντρο \(Κ(1,0)\) και ακτίνα \(ρ_1=3\). Όμοια για την \((2)\) έχουμε
$$Α^2+Β^2-4Γ=36-4\cdot 8=4 > 0,$$
δηλαδή παριστάνει κύκλο με κέντρο \(Λ(3,0)\) και ακτίνα \(ρ_2=1\).
β) i. Έχουμε
$$(ΚΛ)=\sqrt{(3-1)^2+0^2}=2.$$
ii. Δύο κύκλοι με κέντρα \(Κ\), \(Λ\) και ακτίνες \(ρ_1\) και \(ρ_2\), αντίστοιχα, εφάπτονται εσωτερικά αν και μόνο αν
$$(ΚΛ)=|ρ_1-ρ_2|,$$
όπως γνωρίζουμε από την Ευκλείδεια γεωμετρία. Είναι
$$ρ_1-ρ_2=3-1=2$$
και από (β.i) έχουμε
$$(ΚΛ)=2=ρ_1-ρ_2,$$
δηλαδή ικανοποιείται η προϋπόθεση, οπότε ο κύκλος \(C_2\) εφάπτεται εσωτερικά του κύκλου \(C_1\).
γ) Κάθε ακτίνα του κύκλου \(C_1\), \(KA\) και \(KB\) σύμφωνα με το παρακάτω σχήμα, που δεν είναι κάθετη στον \(x'x\) άξονα, είναι πάνω σε ευθεία η οποία διέρχεται από το σημείο \(Κ(1,0)\) έχει κλίση \(λ\in\mathbb{R}\). Άρα έχει εξίσωση
\begin{align}&ε:y-0=λ(x-1)\\ \iff&y-λx+λ=0,\ λ\in\mathbb{R}.\end{align}
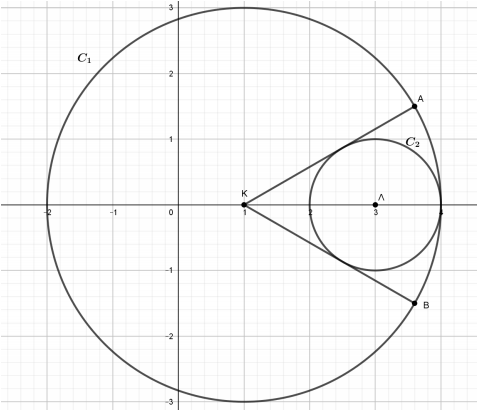
Η \((ε)\) θα εφάπτεται στον \(C_2\) αν και μόνο αν \(d(Λ,ε)=ρ_2\). Έχουμε
\begin{align}&d(Λ,ε)=ρ_2\\ \iff&\frac{|0-3λ+λ|}{\sqrt{1+λ^2}}=1\\ \iff&|2λ|=\sqrt{1+λ^2}\\ \iff&3λ^2=1\\ \iff&λ=\pm\frac{\sqrt{3}}{3}.\end{align}
Τελικά οι ζητούμενες ακτίνες \(ΚΑ\) και \(ΚΒ\) έχουν εξισώσεις
$$ε_1: 3y-\sqrt{3}x+\sqrt{3}=0$$
και
$$ε_2: 3y+\sqrt{3}x-\sqrt{3}=0,$$
αντίστοιχα.
Θέμα: 15081
ΘΕΜΑ 4
Δίνονται οι κύκλοι
$$C_1:x^2+y^2+2\sqrt{2}x+1=0$$
και
$$C_2:x^2+y^2-6\sqrt{2}x+9=0.$$
α) Να δείξετε ότι οι κύκλοι \(C_1\) και \(C_2\) έχουν κέντρα \(Κ(-\sqrt{2},0),\ Λ(3\sqrt{2},0)\) και ακτίνες \(ρ_1=1,\ ρ_2=3\), αντίστοιχα.
(Μονάδες 8)
β) i. Να δείξετε ότι από την αρχή των αξόνων διέρχονται δύο κοινές εφαπτόμενες των κύκλων \(C_1\) και \(C_1\).
(Μονάδες 10)
ii. Να σχεδιάσετε ένα πρόχειρο σχήμα όπου να φαίνονται οι κύκλοι και οι δύο αυτές εφαπτόμενες.
(Μονάδες 7)
Απάντηση Θέματος: 15081
α) Ο κύκλος \(C_1\) έχει κέντρο \(Κ\left(-\dfrac{Α}{2}.-\dfrac{Β}{2}\right)\), δηλαδή \(Κ(-\sqrt{2},0)\) και ακτίνα
$$ρ_1=\frac{\sqrt{Α^2+Β^2-4Γ}}{2}=1$$
και ο κύκλος \(C_2\) έχει κέντρο \(Λ\left(\dfrac{Α}{2},-\dfrac{Β}{2}\right)\), δηλαδή \(Λ(3\sqrt{2},0)\) και ακτίνα
$$ρ_2=\frac{\sqrt{Α^2+Β^2-4Γ}}{2}=3.$$
β) i. Μια ευθεία που διέρχεται από την αρχή των αξόνων \(Ο(0,0)\) και δεν είναι κάθετη στον \(x'x\) άξονα έχει εξίσωση:
$$η:y=λx\iff y-λx=0.$$
Η ευθεία \((η)\) εφάπτεται και στους δύο κύκλους αν και μόνο αν οι αποστάσεις των κέντρων \(Κ\) και \(Λ\) από την ευθεία αυτή είναι ίσες με τις αντίστοιχες ακτίνες των κύκλων. Δηλαδή έχουμε:
$$d(Κ,η)=1\quad(1)$$
και
$$d(Λ,η)=3\quad(2)$$
Λύνουμε το σύστημα των εξισώσεων \((1)\) και \((2)\):
\begin{align}&\begin{cases}\frac{|0+\sqrt{2}λ|}{\sqrt{1+λ^2}}=1\\\frac{|0-3\sqrt{2}λ|}{\sqrt{1+λ^2}}=3\end{cases}\\ \iff&\begin{cases}|\sqrt{2}λ|=\sqrt{1+λ^2}\\|3\sqrt{2}λ|=3\sqrt{1+λ^2}\end{cases}\\ \iff&\begin{cases}2λ^2=1+λ^2\\18λ^2=9+9λ^2\end{cases}\\ \iff&\begin{cases}λ=\pm1\\λ=\pm1\end{cases}\\ \iff&λ=\pm1.\end{align}
Άρα, από την αρχή των αξόνων διέρχονται δυο κοινές εφαπτόμενες των κύκλων, με εξισώσεις
$$η_1:y=-x$$
και
$$η_2:y=x.$$
ii. Η αρχή των αξόνων \((0,0)\) είναι εσωτερικό σημείο της διακέντρου \(ΚΛ\), διότι η \(ΚΛ\) είναι πάνω στον άξονα \(x'x\) και έχει άκρα τα σημεία \(Κ(-\sqrt{2},0)\) και \(Λ(3\sqrt{2},0)\). Επομένως οι εφαπτόμενες που βρήκαμε στο (β.i) ερώτημα είναι εσωτερικές, όπως φαίνεται στο παρακάτω σχήμα.
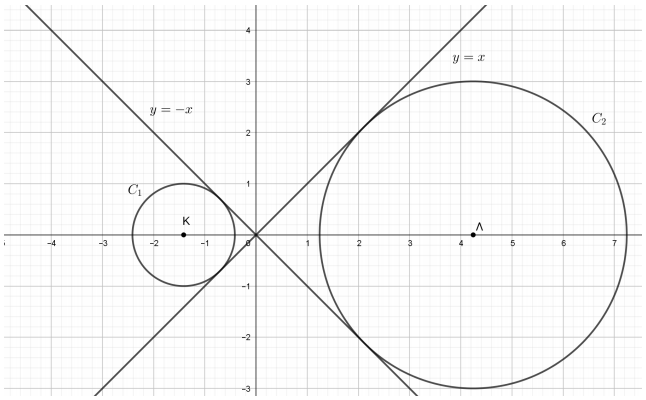
Θέμα: 15082
ΘΕΜΑ 4
Δίνονται δύο κύκλοι με εξισώσεις
$$C_1: (x-2)^2+(y-3)^2=8$$
και
$$C_2: (x-7)^2+(y+2)^2=18.$$
α) Να υπολογίσετε το μήκος της διακέντρου \((ΚΛ)\), όπου \(Κ\), \(Λ\) τα κέντρα των κύκλων \(C_1\), \(C_2\), αντίστοιχα. Ακολούθως να δείξετε ότι οι δύο κύκλοι εφάπτονται εξωτερικά.
(Μονάδες 5)
β) i. Να βρείτε την εξίσωση της ευθείας \(ΚΛ\).
(Μονάδες 5)
ii. Να βρείτε τα σημεία τομής της ευθείας \(ΚΛ\) με τον κύκλο \(C_1\) και το σημείο επαφής των δύο κύκλων.
(Μονάδες 7)
γ) Να βρείτε την εξίσωση της κοινής εσωτερικής εφαπτομένης των κύκλων.
(Μονάδες 8)
Απάντηση Θέματος: 15082
α) Ο κύκλος \(C_1\) έχει κέντρο \(Κ(2,3)\) και ακτίνα \(ρ_1=2\sqrt{2}\), ενώ ο κύκλος \(C_2\) κέντρο \(Λ(7,-2)\) και ακτίνα \(ρ_2=3\sqrt{2}\). Οπότε έχουμε
\begin{align}(KΛ)&=\sqrt{(7-2)^2+(-2-3)^2}\\ &=\sqrt{5^2+5^2}\\ &=5\sqrt{2}.\end{align}
Ακόμα
$$ρ_1+ρ_2=2\sqrt{2}+3\sqrt{2}=5\sqrt{2},$$
δηλαδή \((ΚΛ)=ρ_1+ρ_2\). Αφού η διάκεντρος των δύο κύκλων είναι ίση με το άθροισμα των ακτίνων τους, οι κύκλοι εφάπτονται εξωτερικά.
β) i. Έχουμε
$$λ_{ΚΛ}=\frac{-2-3}{7-2}=-1,$$
οπότε
$$KΛ: y-3=-1(x-2)\iff y=-x+5.$$
ii. Θα βρούμε τα σημεία τομής της ευθείας \(ΚΛ\) με τον κύκλο \(C_1\). Έχουμε:
\begin{align}&\begin{cases}(x-2)^2+(y-3)^2=8\\y=-x+5\end{cases}\\ \iff&\begin{cases}(x-2)^2+(-x+2)^2=8\\y=-x+5\end{cases}\\ \iff&\begin{cases}(x-2)^2=4\\y=-x+5\end{cases}\\ \iff&\begin{cases}x-2=\pm 2\\y=-x+5\end{cases}\\ \iff&\begin{cases}x=4\text{ ή }x=0\\y=1\text{ ή }y=5\end{cases}\end{align}
Οπότε τα κοινά σημεία της \(ΚΛ\) με τον κύκλο \(C_1\) είναι τα \(Α(4,1)\) και \(Α'(0,5)\). Αντίστοιχα έχουμε:
\begin{align}&\begin{cases}(x-7)^2+(y+2)^2=18\\y=-x+5\end{cases}\\ \iff&\begin{cases}(x-7)^2+(-x+7)^2=18\\y=-x+5\end{cases}\\ \iff&\begin{cases}(x-7)^2=9\\y=-x+5\end{cases}\\ \iff&\begin{cases}x-7=\pm 3\\y=-x+5\end{cases}\\ \iff&\begin{cases}x=4\text{ ή }x=10\\y=1\text{ ή }y=-5\end{cases}\end{align}
Οπότε τα κοινά σημεία της ευθείας \(ΚΛ\) με τον κύκλο \(C_2\) είναι τα \(Α(4,1)\) και \(Α΄΄(10,-5)\). Η κοινή λύση και των δύο συστημάτων είναι το ζητούμενο σημείο επαφής των δύο κύκλων. Αλλά το κοινό σημείο της ευθείας και με τους δύο κύκλους είναι το \(A(4,10)\), οπότε αυτό είναι και το σημείο επαφής.
Εναλλακτική λύση:
Βρίσκουμε τα σημεία τομής της ευθείας \(ΚΛ\) με τον κύκλο \(C_1\) λύνοντας το σύστημα
\begin{cases}(x-2)^2+(y-3)^2=8\\y=-x+5\end{cases}
και βρίσκουμε, όπως και στον προηγούμενο τρόπο λύσης, τα σημεία \(Α(4,1)\) και \(Α'(0,5)\). Έχουμε
$$\overrightarrow{ΚΛ}=(7-2,-2-3)=(5,-5)$$
και
$$\overrightarrow{ΚΑ}=(4-2,1-3)=(2,-2),$$
δηλαδή \(\overrightarrow{KA}=\dfrac{2}{5}\overrightarrow{ΚΛ}\), οπότε το \(Α\), ως εσωτερικό σημείο του \(ΚΛ\), είναι το μοναδικό ζητούμενο σημείο επαφής.
γ) Η κοινή εσωτερική εφαπτομένη \((η)\) των δύο κύκλων είναι κάθετη στην ευθεία \(ΚΛ\) και διέρχεται από το σημείο επαφής \(Α(4,1)\). Στο ερώτημα (β.i) έχουμε βρει ότι \(λ_{ΚΛ}=-1\), οπότε
\begin{align}&λ_{η}\cdot λ_{ΚΛ}=-1\\ \iff&λ_η\cdot (-1)=-1\\ \iff&λ_η=1,\end{align}
και η κοινή εσωτερική εφαπτομένη των δύο κύκλων έχει εξίσωση
$$η: y-1=1(x-4)\iff y=x-3.$$
Θέμα: 15177
ΘΕΜΑ 4
Δίνονται τα σημεία \(A(1,0)\) και \(Β(0,-1)\), και ο κύκλος \(c_1\) με εξίσωση
$$c_1:\left(x-\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2=2.$$
α) Να αποδείξετε ότι το σύνολο των σημείων \(N(x,y)\) του επιπέδου τα οποία ικανοποιούν τη σχέση \(\overrightarrow{NA^2}-\overrightarrow{NB^2}=4\) ανήκουν στην ευθεία \((ε)\) με εξίσωση \(y=-x-2\).
(Μονάδες 7)
β) Να αποδείξετε ότι το σύνολο των σημείων \(P\) του επιπέδου τα οποία ικανοποιούν την εξίσωση
$$2x^2+2y^2+10x+14y+21=0$$
ανήκουν σε κύκλο \(c_2\) κέντρου \(Λ\left(-\dfrac{5}{2},-\dfrac{7}{2}\right)\) και ακτίνας \(R=2\sqrt{2}\).
(Μονάδες 6)
γ)
-
Να αποδείξετε ότι οι δύο κύκλοι, \(c_1\) και \(c_2\), εφάπτονται εξωτερικά και στη συνέχεια να βρείτε την ελάχιστη και τη μέγιστη απόσταση των σημείων τους.
(Μονάδες 6) -
Να αποδείξετε ότι η ευθεία \((ε)\) είναι η κοινή εφαπτομένη των κύκλων \(c_1\) και \(c_2\).
(Μονάδες 6)
Απάντηση Θέματος: 15177
α) Θεωρούμε σημείο \(N(x,y)\) του επιπέδου. Είναι \(\overrightarrow{NA}=(1-x,-y)\) και \(\overrightarrow{NB}=(-x,-1-y)\), οπότε ισχύει
\begin{align}&\overrightarrow{NA^2}-\overrightarrow{NB^2}=4\\ \iff&|\overrightarrow{NA}|^2-|\overrightarrow{NB}|^2=4\\ \iff&(1-x)^2+y^2-x^2-(1+y)^2=4\\ \iff&x+y+2=0.\end{align}
Άρα τα ζητούμενα σημεία \(N\) ανήκουν σε ευθεία με εξίσωση \((ε):y=-x-2\).
β) Έστω σημείο \(P(x,y)\) του επιπέδου. Τότε, χρησιμοποιώντας τη μέθοδο συμπλήρωσης τετραγώνου, ισχύει
\begin{align}&2x^2+2y^2+10x+14y+21=0\\ \iff&x^2+y^2+5x+7y+\frac{21}{2}=0\\ \iff&x^2+2x\frac{5}{2}+\left(\frac{5}{2}\right)^2+y^2+2y\frac{7}{2}+\left(\frac{7}{2}\right)^2\\ & =-\frac{21}{2}+\frac{25}{4}+\frac{49}{4}\\ \iff& c_2: \left(x+\frac{5}{2}\right)^2+\left(y+\frac{7}{2}\right)^2=8.\end{align}
Άρα τα σημεία \(P\) ανήκουν πράγματι σε κύκλο \(c_2\) με κέντρο \(Λ\left(-\dfrac{5}{2},-\dfrac{7}{2}\right)\) και ακτίνα \(R=2\sqrt{2}\).
2ος τρόπος:
Έχουμε
\begin{align}&2x^2+2y^2+10x+14y+21=0\\ \iff&x^2+y^2+5x+7y+\frac{21}{2}=0.\end{align}
Αλλά:
$$5^2+7^2-4\cdot\frac{21}{2}=32 > 0$$
επομένως η εξίσωση παραστάνει πράγματι κύκλο, με κέντρο \(Λ\left(-\dfrac{5}{2},-\dfrac{7}{2}\right)\) και ακτίνα \(R=2\sqrt{2}\).
γ)
- Οι κύκλοι \(c_1\) και \(c_2\) εφάπτονται εξωτερικά, διότι έχουν διάκεντρο
\begin{align}δ&=(ΚΛ)\\ &=\sqrt{\left(\dfrac{1}{2}+\dfrac{5}{2}\right)^2+\left(\dfrac{-1}{2}+\dfrac{7}{2}\right)^2}\\ &=3\sqrt{2}\end{align}
και ισχύει \(δ=ρ+R\).
Άρα η ελάχιστη απόσταση των σημείων των δύο κύκλων είναι μηδέν και η μέγιστη απόσταση είναι ίση με \(ΣΤ=ΣΖ+ΖΤ=2ρ+2R=6\sqrt{2}\).
- Είναι
$$d(K,ε)=\frac{|\dfrac{1}{2}-\dfrac{1}{2}+2|}{\sqrt{2}}=\sqrt{2}=ρ$$
και
$$d(Λ,ε)=\frac{|-\dfrac{5}{2}-\dfrac{7}{2}+2|}{\sqrt{2}}=2\sqrt{2}=R.$$
Άρα η ευθεία \((ε)\) είναι η ζητούμενη κοινή εφαπτομένη.
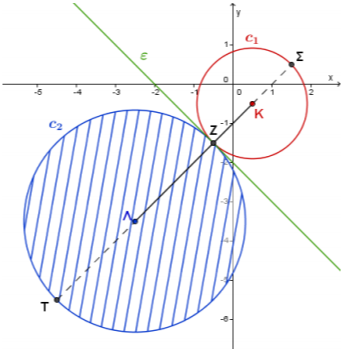
Θέμα: 15189
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(-2,0)\) και \(Β(2,-2)\).
α) Να βρείτε τις συντεταγμένες του μέσου \(Κ\) και το μήκος του ευθυγράμμου τμήματος \(ΑΒ\).
(Μονάδες 6)
β) Να δείξετε ότι ο κύκλος \(C\) με διάμετρο \(ΑΒ\) έχει εξίσωση \(C:x^2+(y+1)^2=5\).
(Μονάδες 6)
γ) Να δείξετε ότι τα σημεία \(M(x,y)\) του επιπέδου για τα οποία \((AMB)=5\) ανήκουν στις ευθείες \(ε_1:x+2y-3=0\) και \(ε_2:x+2y+7=0\).
(Μονάδες 7)
δ) Να δείξετε ότι οι ευθείες \(ε_1\) και \(ε_2\) εφάπτονται του κύκλου \(C\).
(Μονάδες 6)
Απάντηση Θέματος: 15189
α) Το μέσο \(K\) του τμήματος \(AB\) έχει συντεταγμένες \(\left(\dfrac{-2+2}{2},\dfrac{0-2}{2}\right)\), δηλαδή \((0,-1)\). Το μέτρο του διανύσματος \(\overrightarrow{AB}\) είναι
\begin{align}|\overrightarrow{AB}|&=\sqrt{(2-(-2))^2+(-2-0)^2}\\ &=\sqrt{4^2+2^2}\\ &=\sqrt{20}\\ &=2\sqrt{5}.\end{align}
β) Ο κύκλος \(C\) με διάμετρο \(AB\) έχει κέντρο \(K(0,-1)\) και ακτίνα \(ρ=\dfrac{|\overrightarrow{AB}|}{2}=\sqrt{5}\). Άρα η εξίσωση του κύκλου είναι
$$C:x^2+(y+1)^2=5.$$
γ) Έστω \(M(x,y)\). Τότε \((ABM)=\dfrac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AM})|\) με \(\overrightarrow{AM}=(x+2,y)\) και \(\overrightarrow{AB}=(4,-2)\). Οπότε:
\begin{align}&\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AM})|=5\\ \iff&|\!\begin{vmatrix}4&-2\\x+2&y\end{vmatrix}|=10\\ \iff&|4y+2(x+2)|=10\\ \iff&\begin{cases}4y+2x+4=10\\\text{ή}\\4y+2x+4=-10\end{cases}\\ \iff&\begin{cases}2x+4y-6=0\\\text{ή}\\2x+4y+14=0\end{cases}\\ \iff&\begin{cases}x+2y-3=0\\\text{ή}\\x+2y+7=0\end{cases}\end{align}
δ) Για να εφάπτονται οι \(ε_1\) και \(ε_2\) στο κύκλο \(C\) πρέπει
$$d(K,ε_1)=d(K,ε_2)=\sqrt{5}.$$
Είναι
\begin{align}d(K,ε_1)&=\frac{|0+2(-1)-3|}{\sqrt{1^2+2^2}}\\ &=\frac{5}{\sqrt{5}}\\ &=\sqrt{5}\end{align}
και
\begin{align}d(K,ε_1)&=\frac{|0+2(-1)+7|}{\sqrt{1^2+2^2}}\\ &=\frac{5}{\sqrt{5}}\\ &=\sqrt{5}.\end{align}
Θέμα: 15272
ΘΕΜΑ 4
Δίνεται η εξίσωση \(x^2+y^2-2x+4y=-1\).
α) Να αποδείξετε ότι παριστάνει κύκλο του οποίου να βρείτε το κέντρο και την ακτίνα.
(Μονάδες 6)
β) Να αποδείξετε ότι το σημείο \(M(3,2)\) βρίσκεται έξω από τον κύκλο.
(Μονάδες 7)
γ) Να βρείτε τις εφαπτόμενες του κύκλου που διέρχονται από το \(Μ\).
(Μονάδες 12)
Απάντηση Θέματος: 15272
α) Η εξίσωση γράφεται
\begin{align}&x^2-2x+1+y^2+4y+4=4\\ \iff&(x-1)^2+(y+2)^2=4\end{align}
οπότε παριστάνει κύκλο με κέντρο \(K(1,-2)\) και ακτίνα \(ρ=2\).
β) Αρκεί να αποδείξουμε ότι \((ΚΜ) > ρ\). Πραγματικά, είναι
$$(ΚΜ)=\sqrt{(3-1)^2+(2+2)^2}=\sqrt{20}>2$$
οπότε το \(Μ\) βρίσκεται έξω από τον κύκλο.
γ) Όλες οι ευθείες που διέρχονται από το \(Μ\) είναι:
\(\bullet\) Η κατακόρυφη ευθεία \(x=3\). Η ευθεία αυτή απέχει από το κέντρο του κύκλου απόσταση
$$d=\frac{|1-3|}{\sqrt{1+0}}=2=ρ.$$
Άρα η κατακόρυφη ευθεία \(x=3\) εφάπτεται στον κύκλο.
\(\bullet\) Όλες οι μη κατακόρυφες ευθείες που είναι της μορφής \(y-2=λ(x-3)\), δηλαδή \(λx-y-3λ+2=0\). Μια τέτοια ευθεία εφάπτεται στον κύκλο, μόνο όταν η απόσταση \(d\) του κέντρου \(Κ\) από αυτή είναι ίση με την ακτίνα \(ρ\). Είναι:
\begin{align}&d=2\\ \iff&\frac{|λ+2-3λ+2|}{\sqrt{λ^2+1}}=2\\ \iff&\frac{|-2λ+4|}{\sqrt{λ^2+1}}=2\\ \iff&\frac{|λ-2|}{\sqrt{λ^2+1}}=1\\ \iff&λ^2-4λ+4=λ^2+1\\ \iff&λ=\frac{3}{4}\end{align}
Επομένως η άλλη εφαπτομένη του κύκλου που διέρχεται από το \(Μ\) είναι η \(y-2=\dfrac{3}{4}(x-3)\) που γράφεται \(y=\dfrac{3}{4}x-\dfrac{1}{4}\).
Συμπεραίνουμε λοιπόν ότι οι κοινές εφαπτόμενες των δυο κύκλων είναι οι ευθείες με εξισώσεις \(x=3\) και \(y=\dfrac{3}{4}x-\dfrac{1}{4}\).
Θέμα: 15432
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x^2+y^2−4κx−2κy+4=0\quad (1)$$
με \(κ\in\mathbb{R}\).
α) Να βρείτε τις τιμές του \(κ\in\mathbb{R}\) ώστε η εξίσωση \((1)\) να παριστάνει κύκλο.
(Μονάδες 7)
β) Να βρείτε τις συντεταγμένες του κέντρου και την ακτίνα του κάθε κύκλου.
(Μονάδες 3)
γ) Να βρείτε την ευθεία στην οποία ανήκουν τα κέντρα των παραπάνω κύκλων.
(Μονάδες 7)
δ) Για \(κ=1\) να βρείτε την εξίσωση εφαπτομένης του αντίστοιχου κύκλου της εξίσωσης \((1)\) στο σημείο \(Γ(2,2)\).
(Μονάδες 8)
Απάντηση Θέματος: 15432
α) Η εξίσωση \((1)\) είναι της μορφής \(x^2+y^2+Αx+Βy+Γ=0\) και για να παριστάνει κύκλο πρέπει \(Α^2+Β^2-4Γ>0\), όπου \(Α=-4κ, Β=-2κ\) και \(Γ=4\). Άρα
\begin{align}&\phantom{{}={}}Α^2+Β^2-4Γ\\ &=16κ^2+4κ^2-16\\ &=20κ^2-16\end{align}
και
\begin{align}&20κ^2-16>0\\ \iff&κ^2 > \frac{4}{5}\\ \iff&|κ| > \frac{2\sqrt{5}}{5}\\ \iff&κ < -\frac{2\sqrt{5}}{5}\text{ ή }κ > \frac{2\sqrt{5}}{5}.\end{align}
β) Η εξίσωση \((1)\) είναι μία παραμετρική εξίσωση με παράμετρο \(κ\) και \(κ\in\left(-\infty,-\dfrac{2\sqrt{5}}{5}\right)\cup\left(\dfrac{2\sqrt{5}}{5},+\infty\right)\). Για κάθε \(κ\in\left(-\infty,-\dfrac{2\sqrt{5}}{5}\right)\cup\left(\dfrac{2\sqrt{5}}{5},+\infty\right)\) έχουμε έναν κύκλο με κέντρο \(Κ\Big(-\dfrac{Α}{2},-\dfrac{Β}{2}\Big)\), δηλαδή με \(Κ(2κ,κ)\) και ακτίνα
$$ρ=\frac{\sqrt{Α^2+Β^2-4Γ}}{2}=\frac{\sqrt{20κ^2−16}}{2}.$$
γ) Τα κέντρα των κύκλων που προκύπτουν από την παραμετρική εξίσωση \((1)\), από το ερώτημα
(β), έχουν συντεταγμένες \((2κ,κ)\), δηλαδή \(x=2κ\) και \(y=κ\). Άρα
$$x=2y\iff x-2y=0\quad (2),$$
δηλαδή τα κέντρα ανήκουν στην ευθεία με εξίσωση την \((2)\).
δ) Για \(κ=1\) η εξίσωση \((1)\) γίνεται \(x^2+y^2-4x-2y+4=0\), με κέντρο \(Κ(2,1)\) και ακτίνα \(ρ=1\).
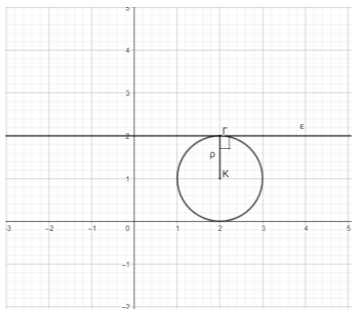
Σε ορθοκανονικό σύστημα αξόνων σχεδιάζουμε τον παραπάνω κύκλο. Η ευθεία που είναι εφαπτομένη στον κύκλο στο σημείο \(Γ\) είναι η ευθεία που είναι κάθετη στο τμήμα \(ΚΓ=ρ\) και παράλληλη στον άξονα \(x'x\), γιατί \(Κ\) και \(Γ\) έχουν την ίδια τετμημένη. Άρα έχει εξίσωση \(y=2\).
Θέμα: 15628
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x^2+y^2+(4-2k)x-2(1+k)y+5-2k=0\quad(1)$$
όπου \(k\in(0,+\infty)\).
α) Να αποδείξετε ότι η \((1)\) παριστάνει κύκλο με κέντρο \(M(k-2,k+1)\) και ακτίνα \(k\sqrt{2}\) για κάθε \(k > 0\).
(Μονάδες 10)
β) Να αποδείξετε ότι το σημείο \(M\) ανήκει σε μια σταθερή ευθεία για κάθε \(k > 0\).
(Μονάδες 7)
γ) Να αποδείξετε ότι η ευθεία \((ε):y=-x-1\) είναι εφαπτομένη του παραπάνω κύκλου για κάθε \(k > 0\).
(Μονάδες 8)
Απάντηση Θέματος: 15628
α) Παρατηρούμε ότι η \((1)\) είναι στη μορφή \(x^2+y^2+Αx+Βy+Γ=0\), με
\begin{align} &\phantom{{}={}}Α^2+Β^2-4Γ\\ &=(4-2k)^2+[-2(1+k)]^2-4\cdot(5-2k)\\ &=16-16k+4k^2+4+8k+4k^2-20+8k\\ &=8k^2.\end{align}
Αφού \(Α^2+Β^2-4Γ > 0\), η \((1)\) παριστάνει κύκλο με ακτίνα
$$ρ=\frac{\sqrt{8k^2}}{2}=\frac{2\sqrt{2}k}{2}=k\sqrt{2}$$
και κέντρο
\begin{align}&\phantom{{}={}}Μ\left(-\frac{Α}{2} ,-\frac{Β}{2}\right)\\ &=Μ\left(-\frac{4-2κ}{2}, -\frac{-2(1+k)}{2}\right)\\ &=Μ(k-2,k+1).\end{align}
Καθώς η παράμετρος \(k\) παίρνει άπειρες τιμές, έχουμε άπειρους κύκλους.
β) Ας είναι \(x\) η τετμημένη των σημείων \(Μ\) και \(y\) η τεταγμένη των σημείων \(Μ\). Τότε \(x=k-2, y=k+1\), ώστε \(y=(x+2)+1\). Άρα \(y=x+3\), η εξίσωση της ευθείας πάνω στην οποία ανήκουν τα σημεία \(Μ\).
γ) Προφανώς αρκεί να δείξουμε ότι η απόσταση των κέντρων \(Μ\) από την σταθερή ευθεία \((ε):x+y+1=0\) ισούται με την ακτίνα. Πράγματι
\begin{align}d(Μ,ε)&=\frac{|1(k-2)+1(k+1)+1|}{\sqrt{1^2+1^2}}\\ &=\frac{|2k|}{\sqrt{2}}\\ &=k\sqrt{2}.\end{align}
Θέμα: 15646
ΘΕΜΑ 4
Δίνονται οι κύκλοι
$$C_1: (x-1)^2+(y-1)^2=9$$
και
$$C_2: (x-4)^2+(y-4)^2=9.$$
α) Να δείξετε ότι τα κέντρα \(Κ\), \(Λ\) των κύκλων \(C_1\) και \(C_2\), αντίστοιχα, βρίσκονται στη διχοτόμο της γωνίας \(x\hat{O}y\) του συστήματος συντεταγμένων.
(Μονάδες 8)
β) Να βρείτε τα σημεία τομής \(Β\), \(Γ\) των κύκλων \(C_1\) και \(C_2\).
(Μονάδες 7)
γ) Να βρείτε τα σημεία της ευθείας \(y=x\) ώστε το τρίγωνο που ορίζεται με τα \(Β\), \(Γ\) να έχει εμβαδόν \(\frac{21}{2}\).
(Μονάδες 10)
Απάντηση Θέματος: 15646
α) Ο κύκλος \(C_1\) έχει κέντρο \(K(1,1)\) και ακτίνα \(ρ=3\), ενώ ο κύκλος \(C_2\) έχει κέντρο \(Λ(4,4)\) και ακτίνα \(ρ=3\). Έχουμε
$$λ_{ΚΛ}=\frac{4-1}{4-1}=1,$$
άρα η \(ΚΛ\) βρίσκεται στην ευθεία με εξίσωση
$$y-1=1(x-1)\iff y=x,$$
δηλαδή η διάκεντρος βρίσκεται στην διχοτόμο της γωνίας \(x\hat{O}y\).
β) Για να βρούμε τα σημεία τομής των κύκλων \(C_1\) και \(C_2\) θα λύσουμε το σύστημα των εξισώσεών τους. Αφαιρώντας κατά μέλη παίρνουμε
\begin{align}&(x-1)^2+(y-1)^2-(x-4)^2-(y-4)^2=0\\ \iff&(x-1)^2-(x-4)^2=(y-4)^2-(y-1)^2\\ \iff&3(2x-5)=-3(2y-5)\\ \iff&2x-5=5-2y\\ \iff&y=5-x.\end{align}
Αντικαθιστώντας την τιμή του \(y\) στην εξίσωση του \(C_1\), βρίσκουμε
\begin{align}&(x-1)^2+(4-x)^2=9\\ \iff&2x^2-10x+8=0\\ \iff&x^2-5x+4=0\\ \iff&x_1=1,x_2=4\end{align}
με τις αντίστοιχες τιμές \(y_1=4\), \(y_2=1\). Τελικά τα σημεία τομής των κύκλων \(C_1\) και \(C_2\) είναι \(Β(1,4)\) και \(Γ(4,1)\).
γ) Το σημείο \(Α(x,y)\) ανήκει στην ευθεία που ανήκουν τα σημεία \(Κ\) και \(Λ\) με εξίσωση, όπως βρήκαμε στο (α) ερώτημα, \(y=x\) αν και μόνο αν οι συντεταγμένες του επαληθεύουν την εξίσωση. Οπότε έχουμε \(A(x,x)\). Είναι
$$\overrightarrow{AB}=(1-x,4-x)$$
και
$$\overrightarrow{AΓ}=(4-x,1-x).$$
Ακόμα,
\begin{align}(ΑΒΓ)&=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{AΓ})|\\ &=\frac{1}{2}|\!\begin{vmatrix}1-x&4-x\\4-x&1-x\end{vmatrix}|\\ &=\frac{1}{2}|(1-x)^2-(4-x)^2|\\ &=\frac{1}{2}|6x-15|.\end{align}
Οπότε
\begin{align}&(ΑΒΓ)=\frac{21}{2}\\ \iff&\frac{1}{2}|6x-15|=\frac{21}{2}\\ \iff&|6x-15|=21\\ \iff&6x-15=\pm 21\\ \iff&x=6\text{ ή }x=-1.\end{align}
Τελικά βρήκαμε δύο σημεία της ευθείας \(y=x\), τα \(Α(6,6)\) και \(Α'(-1,-1)\), που ορίζουν με τα σημεία τομής \(Β\) και \(Γ\) τρίγωνο εμβαδού \(\dfrac{21}{2}\), όπως φαίνεται στο παρακάτω σχήμα.
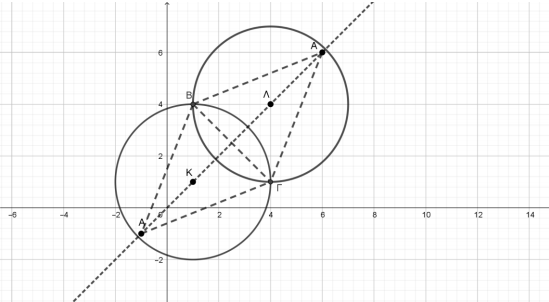
Θέμα: 15680
ΘΕΜΑ 2
Δίνεται ο κύκλος \(C:\ x^2+y^2-2x-4y+1=0\) με κέντρο \(K(1,2)\) και η ευθεία \((ε):\ 3x+4y+1=0.\)
α) Να αποδείξετε ότι η ακτίνα του κύκλου \(C\) είναι \(ρ=2\). (Μονάδες 10)
β) Να αποδείξετε ότι η απόσταση του κέντρου \(Κ\) από την ευθεία \((ε)\) είναι \(\dfrac{12}{5}\).
(Μονάδες 10)
γ) Να αιτιολογήσετε γιατί η ευθεία \((ε)\) και ο κύκλος \(C\) δεν έχουν κοινά σημεία.
(Μονάδες 5)
Απάντηση Θέματος: 15680
α) Είναι
$$\begin{align} ρ & =\dfrac{\sqrt{Α^2+Β^2-4Γ}}{2}\\ &=\dfrac{\sqrt{(-2)^2+(-4)^2-4\cdot 1}}{2}\\ &=2.\end{align}$$
β) Είναι
$$d(Κ,ε)=\dfrac{|3\cdot 1+4\cdot 2+1|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}.$$
γ) Αφού \(d(Κ,ε)=\dfrac{12}{5}>ρ\) η ευθεία \((ε)\) και ο κύκλος \(C\) δεν έχουν κοινά σημεία.
Θέμα: 15791
ΘΕΜΑ 4
Στο παρακάτω σχήμα έχουμε σχεδιάσει κύκλο \(C_1\) κέντρου \(A\) και την ευθεία \((ε):\ x=5\).
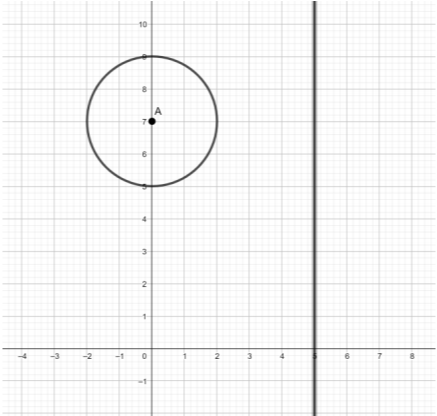
α) Να βρείτε την εξίσωση του κύκλου \(C_1\).
(Μονάδες 3)
β) Έστω ένα σημείο του επιπέδου, \(B(x_1,y_1)\).
i. Να βρείτε την εξίσωση του κύκλου με κέντρο \(B(x_1,y_1)\) και ακτίνα \(2\).
(Μονάδες 6)
ii. Να βρείτε το μήκος της διακέντρου \(AB\) σε συνάρτηση με τις συντεταγμένες του σημείου \(B\).
(Μονάδες 6)
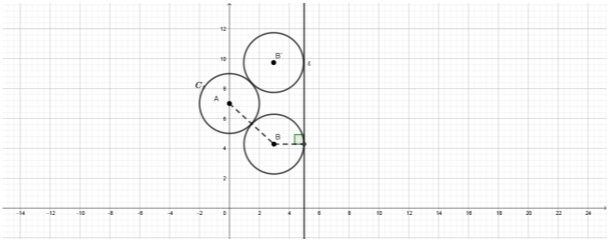
γ) Να βρείτε όλους τους κύκλους του ερωτήματος (β.i) με ακτίνα \(2\), που εφάπτονται εξωτερικά στον \(C_1\) και στην ευθεία \(ε\).
(Μονάδες 10)
Απάντηση Θέματος: 15791
α) Ο κύκλος \(C_1\) έχει κέντρο \(A(0,7)\) και ακτίνα \(ρ=2\), άρα αντικαθιστώντας στον τύπο
$$(x-x_0)^2+(y-y_0)^2=ρ^2$$
τις αντίστοιχες τιμές έχουμε
\begin{align}&(x-0)^2+(y-7)^2=2^2\\ \iff&x^2+(y-7)^2=4,\end{align}
που είναι η ζητούμενη εξίσωση του κύκλου \(C_1\).
β) i. Σύμφωνα με τον τύπο
$$(x-x_0)^2+(y-y_0)^2=ρ^2,$$
οι κύκλοι με κέντρο \(B(x_1,y_1)\) και ακτίνα \(2\) έχουν εξίσωση
$$(x-x_1)^2+(y-y_1)^2=4.$$
ii. Η απόσταση δύο σημείων \(A(x_A,y_A)\) και \(B(x_B,y_B)\) δίνεται από τον τύπο
$$(AB)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2},$$
οπότε για τα σημεία \(A(0,7)\) και \(B(x_1,y_1)\) έχουμε
\begin{align}&(AB)=\sqrt{(0-x_1)^2+(7-y_1)^2}\\ \iff&(AB)=\sqrt{x_1^2+(7-y_1)^2}.\end{align}
γ) Δύο κύκλοι εφάπτονται εξωτερικά αν και μόνο αν η διάκεντρος είναι ίση με το άθροισμα των ακτίνων τους. Οπότε έχουμε
\begin{align}&(AB)=2+2\\ \iff&\sqrt{x_1^2+(y_1-7)^2}=4\\ \iff&x_1^2+(y_1-7)^2=16.\quad(1)\end{align}
Ένας κύκλος εφάπτεται σε ευθεία αν και μόνο αν το κέντρο του κύκλου απέχει από την ευθεία απόσταση ίση με την ακτίνα του. Οπότε έχουμε
\begin{align}&d(B,ε)=2\\ \iff&\frac{|0+x_1-5|}{\sqrt{0^2+1^2}}=2\\ \iff&|x_1-5|=2.\quad(2)\end{align}
Για να βρούμε τους κύκλους που εφάπτονται στον κύκλο \(C_1\) και στην ευθεία \((ε)\), επιλύουμε το σύστημα των εξισώσεων \((1)\) και \((2)\):
\begin{align}&\begin{cases}x_1^2+(y_1-7)^2=16\\|x_1-5|=2\end{cases}\\ \iff&\begin{cases}x_1^2+(y_1-7)^2=16\\x_1-5=\pm2\end{cases}\\ \iff&\begin{cases}\begin{cases}7^2+(y_1-7)^2=16\\x_1=7\end{cases}\\\qquad\text{ή}\\\begin{cases}3^2+(y_1-7)^2=16\\x_1=3\end{cases}\end{cases}\\ \iff&\begin{cases}\begin{cases}(y_1-7)^2=-33\\x_1=7\end{cases}\text{ (αδύνατο)}\\\qquad\text{ή}\\\begin{cases}(y_1-7)^2=7\\x_1=3\end{cases}\end{cases}\\ \iff&\begin{cases}y_1=7\pm\sqrt{7}\\x_1=3\end{cases}\end{align}
Τελικά είναι δύο οι κύκλοι ακτίνας \(2\) που εφάπτονται εξωτερικά στον κύκλο \(C_1\) και στην ευθεία \((ε)\). Έχουν κέντρα \(B(3,7-\sqrt{7})\) και \(B'(3,7+\sqrt{7})\).
Θέμα: 15826
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x^2+y^2-2(λ+1)x-2λy+2λ+1=0\quad (1)$$
όπου \(λ\in\mathbb{R}\).
α) Να βρείτε για ποιες τιμές του \(λ\) η εξίσωση \((1)\) παριστάνει κύκλο και να γράψετε ως συνάρτηση του \(λ\) τις συντεταγμένες του κέντρου \(Κ\) και την ακτίνα \(ρ\).
(Μονάδες 7)
β) Τι παριστάνει η εξίσωση \((1)\) για \(λ=0\);
(Μονάδες 3)
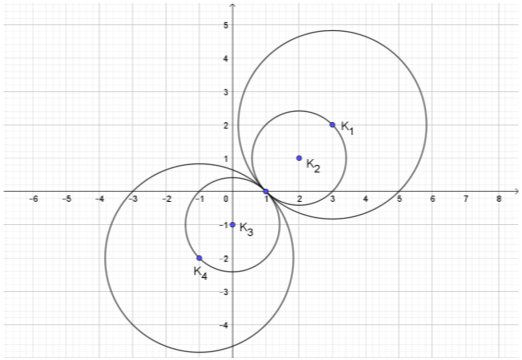
γ) Στο παρακάτω σχήμα φαίνονται \(4\) κύκλοι με τα αντίστοιχα κέντρα τους \(Κ_1,Κ_2,Κ_3,Κ_4\) που προκύπτουν από την \((1)\) για \(4\) αντίστοιχες τιμές του \(λ\). Αξιοποιώντας το σχήμα,
i. να αποδείξετε ότι τα κέντρα όλων των κύκλων που προκύπτουν από την \((1)\) βρίσκονται πάνω σε μια ευθεία της οποίας να βρείτε την εξίσωση.
(Μονάδες 5)
ii. να αποδείξετε ότι όλοι οι κύκλοι που προκύπτουν από την \((1)\) διέρχονται από σταθερό σημείο του οποίου να βρείτε τις συντεταγμένες.
(Μονάδες 5)
iii. να αποδείξετε ότι η ευθεία \(ε:x+y-1=0\) είναι κοινή εφαπτομένη όλων των κύκλων που προκύπτουν από την \((1)\).
(Μονάδες 5)
Απάντηση Θέματος: 15826
α) Η \((1)\) είναι της μορφής \(x^2+y^2+Αx+Βy+Γ=0\), όπου \(Α=-2(λ+1), Β=-2λ\) και \(Γ=2λ+1\). Είναι
\begin{align}&\phantom{{}={}}Α^2+Β^2-4Γ\\ &=(-2(λ+1))^2+(-2λ)^2-4(2λ+1)\\ &=4λ^2+8λ+4+4λ^2-8λ-4\\ &=8λ^2.\end{align}
Για να παριστάνει η \((1)\) κύκλο πρέπει και αρκεί
$$Α^2+Β^2-4Γ > 0\iff 8λ^2 > 0\iff λ\neq 0.$$
Το κέντρο είναι το \(Κ\left(-\dfrac{Α}{2},-\dfrac{Β}{2}\right)\), δηλαδή \(Κ(λ+1,λ)\), και η ακτίνα
\begin{align}ρ&=\frac{\sqrt{Α^2+Β^2-4Γ}}{2}\\ &=\frac{\sqrt{8λ^2}}{2}\\ &=\frac{2\sqrt{2}|λ|}{2}\\ &=\sqrt{2}|λ|.\end{align}
β) Για \(λ=0\) η \((1)\) γίνεται
\begin{align}&x^2+y^2-2x+1=0\\ \iff&(x-1)^2+y^2=0\\ \iff&x=1\text{ και }y=0\end{align}
που σημαίνει ότι παριστάνει το σημείο \(Μ(1,0)\).
γ) i. Η ευθεία που διέρχεται από τα κέντρα \(Κ_1,Κ_2\) του σχήματος έχει συντελεστή διεύθυνσης
$$λ=\frac{y_{Κ_1}-y_{Κ_2}}{x_{Κ_1}-x_{Κ_2}}=\frac{2-1}{3-2}=1$$
και εξίσωση
$$(ζ):y-1=1(x-2)\iff y=x-1.$$
Θα αποδείξουμε ότι τα κέντρα όλων των κύκλων που προκύπτουν από την \((1)\) βρίσκονται πάνω στην ευθεία \((ζ)\). Πράγματι, το τυχόν κέντρο \(Κ(λ+1,λ)\) ανήκει στην ευθεία \((ζ)\), αφού οι συντεταγμένες του επαληθεύουν την εξίσωση \(y=x-1\).
ii. Οι κύκλοι του σχήματος διέρχονται από το σημείο \(Μ(1,0)\). Θα αποδείξουμε ότι όλοι οι κύκλοι που προκύπτουν από την \((1)\) διέρχονται από το \(Μ(1,0)\). Πράγματι, οι συντεταγμένες του \(Μ\) επαληθεύουν την \((1)\) για κάθε \(λ\in \mathbb{R}\), αφού
$$1^2+0^2-2(λ+1)\cdot 1-2λ\cdot 0+2\cdot λ+1=0\iff 0=0$$
που ισχύει.
iii. Θα πρέπει το κέντρο \(Κ(λ+1,λ)\) να απέχει από την ευθεία \(ε:x+y-1=0\) απόσταση ίση με την ακτίνα \(ρ\). Πράγματι,
\begin{align}d(Κ,ε)&=\frac{|λ+1+λ-1|}{\sqrt{1^2+1^2}}\\ &=\frac{2|λ|}{\sqrt{2}}\\ &=\sqrt{2}|λ|\\ &=ρ.\end{align}
Σημείωση:
Η ευθεία \(ε:x+y-1=0\) διέρχεται από το σημείο \(Μ(0,1)\) και είναι κάθετη στην ευθεία \(ζ\), όπως φαίνεται και στο παρακάτω σχήμα.

Θέμα: 15993
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$(x-2)^2+(y-λ)^2=λ^2+1\quad(1)$$
όπου \(λ\in\mathbb{R}\).
α) Να αποδείξετε ότι για κάθε τιμή του \(λ\) η \((1)\) παριστάνει κύκλο, του οποίου να βρείτε το κέντρο και την ακτίνα.
(Μονάδες 3)
β) Να αποδείξετε ότι όλοι οι κύκλοι που ορίζονται από την \((1)\) για τις διάφορες τιμές του \(λ\) διέρχονται από δύο σταθερά σημεία.
(Μονάδες 10)
γ) Αν \(Α(1,0)\) και \(Β(3,0)\) είναι τα μοναδικά σημεία από τα οποία διέρχονται όλοι οι κύκλοι, τότε να βρείτε την εξίσωση της κοινής χορδής τους και να αποδείξετε ότι είναι κάθετη στην ευθεία που διέρχεται από τα κέντρα των κύκλων.
(Μονάδες 7)
δ) Αν ένα σημείο \(Μ(α,β)\) επαληθεύει την \((1)\) για κάθε \(λ\in\mathbb{R}\), τότε να αποδείξετε ότι \(α\cdot β=0\).
(Μονάδες 5)
Απάντηση Θέματος: 15993
α) Είναι γνωστό ότι η εξίσωση
$$(x-x_0)^2+(y-y_0)^2=ρ^2$$
παριστάνει κύκλο με κέντρο το \(K(x_0,y_0)\) και ακτίνα \(ρ > 0\). Η \((1)\) γράφεται
$$(x-2)^2+(y-λ)^2=(\sqrt{λ^2+1})^2,$$
επομένως παριστάνει κύκλο με κέντρο το \(K(2,λ)\) και ακτίνα \(ρ=\sqrt{λ^2+1}\), διότι \(λ^2+1 > 0\) για κάθε \(λ\in\mathbb{R}\).
β) Επιλέγουμε δύο από τους κύκλους \((1)\), δίνοντας τις παρακάτω τιμές:
Για \(λ=0\),
$$x^2+y^2-4x+3=0.$$
Για \(λ=1\),
$$x^2+y^2-4x-2y+3=0.$$
Αφαιρώντας κατά μέλη τις δύο ισότητες προκύπτει \(y=0\) και αντικαθιστώντας στην πρώτη εξίσωση, είναι
\begin{align}&x^2-4x+3=0\\ \iff&x=1\text{ ή }x=3.\end{align}
Επομένως οι κύκλοι έχουν δύο κοινά σημεία, τα \(A(1,0)\) και \(B(3,0)\). Με μια απλή αντικατάσταση στην \((1)\), αποδεικνύεται ότι τα σημεία αυτά την επαληθεύουν για κάθε \(λ\in\mathbb{R}\), και ως εκ τούτου αποτελούν τα κοινά σημεία όλων των κύκλων.
γ) Η κοινή χορδή των κύκλων \((1)\) είναι το ευθύγραμμο τμήμα \(ΑΒ\), το οποίο βρίσκεται πάνω στον άξονα \(x'x\). Επομένως έχει εξίσωση \(y=0\). Τα κέντρα όλων των κύκλων είναι της μορφής \(Κ(2,λ)\) με \(λ\in\mathbb{R}\). Άρα, η ευθεία που διέρχεται από τα κέντρα όλων των κύκλων είναι η κατακόρυφη ευθεία με εξίσωση \(x=2\). Επομένως είναι κάθετη στην κοινή χορδή.
δ) Αφού το σημείο \(Μ(α,β)\) επαληθεύει την \((1)\) για κάθε \(λ\in\mathbb{R}\), πρέπει υποχρεωτικά να είναι ή το \(Α(1,0)\) ή το \(Β(3,0)\). Σε κάθε περίπτωση ισχύει
$$α\cdot β=1\cdot 0=3\cdot 0=0.$$
Θέμα: 15994
ΘΕΜΑ 2
Δίνεται η εξίσωση \(x^2+y^2-4x+3=0,\ (1).\)
α) Να αποδείξετε ότι η εξίσωση \((1)\) παριστάνει κύκλο του οποίου να βρείτε το κέντρο και την ακτίνα.
(Μονάδες 13)
β) Να σχεδιάσετε τον κύκλο \((C)\) και να βρείτε, χρησιμοποιώντας το σχήμα ή με οποιανδήποτε άλλον τρόπο, τα κοινά του σημεία με τους άξονες.
(Μονάδες 12)
Απάντηση Θέματος: 15994
α) Ως γνωστόν, η εξίσωση \(x^2+y^2+Ax+Βy+Γ=0\) με \(Α^2+Β^2-4Γ>0\) παριστάνει κύκλο, με κέντρο \(Κ\Big( -\dfrac{A}{2}, -\dfrac{B}{2}\Big)\) και ακτίνα \(ρ=\dfrac{\sqrt{Α^2+Β^2-4Γ}}{2}.\)
Επειδή \((-4)^2-4\cdot 3=4>0\), η \((1)\) παριστάνει κύκλο.
Τότε \(-\dfrac{A}{2}=2\) και \(-\dfrac{B}{2}=0.\) Το κέντρο του λοιπόν είναι το σημείο \(Κ(2,0)\), η ακτίνα του είναι \(ρ=1\), οπότε η εξίσωση του γράφεται ισοδύναμα: \((C):\ (x-2)^2+y^2=1,\ (2).\)
β) Η γραφική παράσταση του ζητούμενου κύκλου είναι η παρακάτω.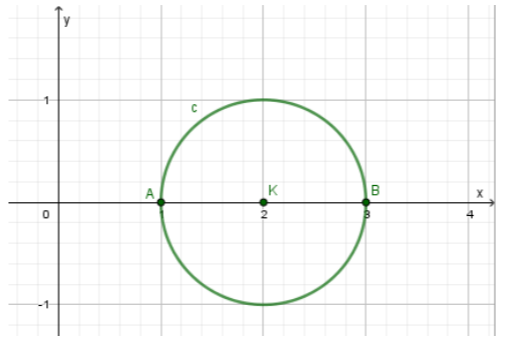
Εναλλακτική λύση:
Από την εξίσωση του κύκλου, για \(y=0\) έχουμε:
$$(x-2)^2=1$$ $$\Leftrightarrow x-2=1 \text{ ή } x-2=-1$$ $$\Leftrightarrow x=3 \text{ ή } x=1$$
Επομένως ο κύκλος τέμνει τον άξονα \(x'x\) στα σημεία \(A(1,0)\) και \(B(3,0).\) Για \(x=0\) η εξίσωση είναι αδύνατη, οπότε ο κύκλος δεν έχει κοινό σημείο με τον άξονα \(y'y.\)
Θέμα: 16191
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(1,1), Β(5,5)\).
α) Αν για το σημείο \(Μ(x,y)\) ισχύει \(\overrightarrow{ΑΜ}^2+\overrightarrow{ΒΜ}^2=32\), να αποδείξετε ότι:
i. Το σημείο \(Μ\) βρίσκεται πάνω στην καμπύλη με εξίσωση
$$x^2+y^2-6x-6y+10=0.\quad(1)$$
(Μονάδες 8)
ii. Η εξίσωση \((1)\) παριστάνει κύκλο.
(Μονάδες 3)
β) Αν το κέντρο του κύκλου είναι το \(Κ(3,3)\) και η ακτίνα του \(ρ=2\sqrt{2\):
i. Nα διερευνήσετε για ποιες τιμές του \(λ\) η ευθεία \(ε:λx+y=2\) εφάπτεται του κύκλου \((1)\).
(Μονάδες 7)
ii. Υπάρχει τιμή του \(λ\) για την οποία η ευθεία \((ε)\) σχηματίζει με την \(ΑΒ\) γωνία \(45^ο\);
(Μονάδες 7)
Απάντηση Θέματος: 16191
α) i. Είναι \(\overrightarrow{ΑΜ}=(x-1,y-1)\) και \(\overrightarrow{ΒΜ}=(x-5,y-5)\). Άρα
\begin{align}&\overrightarrow{ΑΜ}^2+\overrightarrow{ΒΜ}^2=32\\ \iff&\sqrt{(x-1)^2+(y-1)^2}+\sqrt{(x-5)^2+(y-5)^2}^2=32\\ \iff&x^2-2x+1+y^2-2y+1+x^2-10x+25+y^2-10y+25=32\\ \iff&2x^2+2y^2-12x-12y+20=0\\ \iff&x^2+y^2-6x-6y+10=0.\quad(1)\end{align}
ii. Για να παριστάνει η εξίσωση \(x^2+y^2+Αx+Βy+Γ=0\) κύκλο θα πρέπει \(Α^2+Β^2-4Γ > 0\). Από την \((1)\) έχουμε \(Α=-6, Β =-6\) και \(Γ=10\). Συνεπώς
$$Α^2+Β^2-4Γ=6^2+6^2-4\cdot 10=32 > 0.$$
Επομένως πρόκειται περί κύκλου.
β) i. Για να εφάπτεται ο κύκλος στην ευθεία, πρέπει η απόσταση του κέντρου \(Κ\) από την ευθεία να ισούται με την ακτίνα του κύκλου. Είναι
\begin{align}&d(K,ε)=ρ\\ \iff&\frac{|3λ+3-2|}{\sqrt{λ^2+1}}=2\sqrt{2}\\ \iff&|3λ+1|=2\sqrt{2}\sqrt{λ^2+1}\\ \iff&(3λ+1)^2=8(λ^2+1)\\ \iff&9λ^2+6λ+1=8λ^2+8\\ \iff&λ^2+6λ-7=0.\end{align}
Υπολογίζουμε τις ρίζες και έχουμε \(λ=-7\) και \(λ=1\).
ii. Ο συντελεστής διεύθυνσης της \(ΑΒ\) είναι
$$λ_{ΑΒ}=\frac{y_Β-y_Α}{x_Β-x_Α}=\frac{5-1}{5-1}=1.$$
Ένα διάνυσμα παράλληλο στην \(ΑΒ\) είναι το \(\vec{δ}_1=(1,1)\) ενώ ένα διάνυσμα παράλληλο στην \((ε)\) είναι το \(\vec{δ}_2=(1,-λ)\). Η γωνία των δύο ευθειών είναι η γωνία των δύο διανυσμάτων που είναι παράλληλα σε αυτές. Έχουμε
\begin{align}&συν(\widehat{\vec{δ}_1,\vec{δ}_2})=συν45^ο\\ \iff&\frac{\vec{δ}_1\cdot\vec{δ}_2}{|\vec{δ}_1||\vec{δ}_2|}=\frac{\sqrt{2}}{2}\\ \iff&\frac{(1,1)\cdot(1,-λ)}{\sqrt{1^2+1^2}\sqrt{1^2+λ^2}}=\frac{\sqrt{2}}{2}\\ \iff&\frac{1-λ}{\sqrt{2}\sqrt{1+λ^2}}=\frac{\sqrt{2}}{2}\\ \iff&2(1-λ)=\sqrt{2}\sqrt{2}\sqrt{1+λ^2}\\ \iff&2(1-λ)=2\sqrt{1+λ^2}\\ \iff&1-λ=\sqrt{1+λ^2}\\ \implies&(1-λ)^2=(\sqrt{1+λ^2})^2,\ (2)\\ \iff&1-2λ+λ^2=1+λ^2\\ \iff&λ=0.\end{align}
Εφόσον \(λ=0 < 1\), η συνεπαγωγή που δίνει τη σχέση \((2)\) είναι και αυτή ισοδυναμία, οπότε έχουμε το ζητούμενο.
Θέμα: 16773
ΘΕΜΑ 2
α) Να βρεθεί η εξίσωση του κύκλου που έχει κέντρο το \(Ο(0,0)\) και διέρχεται από το σημείο \(Α(1,2)\).
(Μονάδες 8)
β) Δίνεται ο κύκλος \(x^2+y^2=5\).
i. Να βρεθεί η εξίσωση της εφαπτόμενής του στο σημείο \(Α\).
(Μονάδες 9)
ii. Να βρεθεί το σημείο \(Β\), το οποίο είναι αντιδιαμετρικό του \(Α\) σε αυτόν τον κύκλο.
(Μονάδες 8)
Απάντηση Θέματος: 16773
α) Η εξίσωση κύκλου με κέντρο το \(Ο(0,0)\) είναι \(x^2+y^2=ρ^2\ (1)\), όπου \(ρ\) η ακτίνα του κύκλου. Επειδή ο κύκλος διέρχεται από το σημείο \(Α(1,2)\) θα πρέπει οι συντεταγμένες του \(Α\) να επαληθεύουν την εξίσωση \((1)\), δηλαδή \(1^2+2^2=ρ^2\), άρα \(ρ^2=5\). Οπότε, η \((1)\) γίνεται:
$$x^2+y^2=5.$$
β) i. Η εξίσωση της εφαπτομένης του κύκλου \((1)\) στο σημείο του \(A(x_1,y_1)\) είναι:
$$xx_1+yy_1=ρ^2\quad(2)$$
Έτσι η εξίσωση της εφαπτομένης του κύκλου \(x^2+y^2=5\) στο σημείο του \(A(1,2)\) θα είναι \(x+2y=5\).
ii. Για να είναι το σημείο \(Β\) αντιδιαμετρικό του \(Α\), θα πρέπει το κέντρο \(Ο\) να είναι το μέσο του τμήματος \(ΑΒ\). Επομένως θα ισχύουν:
\begin{align}&\begin{cases}x_0=\frac{x_A+x_B}{2}\\y_0=\frac{y_A+y_B}{2}\end{cases}\\ \iff&\begin{cases}0=\frac{1+x_B}{2}\\0=\frac{2+y_B}{2}\end{cases}\\ \iff&\begin{cases}0=1+x_B\\0=2+y_B\end{cases}\\ \iff&\begin{cases}x_B=-1\\y_B=-2\end{cases}.\end{align}
Άρα είναι \(Β(-1,-2)\).
Θέμα: 16808
ΘΕΜΑ 2
Δίνονται τα σημεία του επιπέδου \(Α(-8, 1),\ Β(4, 5)\) και \(Γ(-4, 9)\).
α) Να βρείτε τις συντεταγμένες του μέσου \(K\) του ευθύγραμμου τμήματος \(ΑΒ\).
(Μονάδες 8)
β) Μα δείξετε ότι ο κύκλος (\(C\)) που έχε κέντρο το σημείο \(Κ\) κα διάμετρο το τμήμα \(ΑΒ\) διέρχεται από το σημείο \(Γ\).
(Μονάδες 9)
β) Να βρείτε την εξίσωση του κύκλου (\(C\)).
(Μονάδες 10)
Απάντηση Θέματος: 16808
α) Το μέσο \(Κ\) του τμήματος \(ΑΒ\) έχει συντεταγμένες \(\Bigg( \dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2} \Bigg)\).
Άρα \(Κ\Bigg( \dfrac{-8+4}{2}, \dfrac{1+5}{2} \Bigg) = (-2, 3).\)
β) Αρκεί να δείξουμε ότι, το μέσο \(Κ\) του τμήματος \(ΑΒ\) απέχει από το σημείο \(Γ\) απόσταση ίση με το μισό του τμήματος \(ΑΒ\). Δηλαδή \(ΚΓ = \dfrac{ΑΒ}{2}\).
Το μήκος του τμήματος \(ΑΒ\) είναι:
$$\begin{align} (ΑΒ) & = \sqrt{(-8-4)^2+(1-5)^2} \\ & = \sqrt{144+16} \\ & = \sqrt{160} \\ & = 4 \sqrt{10} \end{align}$$
Το μήκος του τμήματος \(ΚΓ\) είναι:
$$\begin{align} (ΚΓ) & = \sqrt{(-2+4)^2+(3-9)^2} \\ & = \sqrt{4+36} \\ & = \sqrt{40} \\ & = 2 \sqrt{10} \\ & = \dfrac{AB}{2}. \end{align}$$
γ) Το κέντρο του κύκλου είναι το σημείο \(Κ(-2,3)\) και η ακτίνα του \(ρ= \dfrac{ΑΒ}{2}=2 \sqrt{10}\).
Άρα η εξίσωση του κύκλου είναι \((C):\ (x+2)^2 + (y-3)^2 = 40\).
Θέμα: 17317
ΘΕΜΑ 2
Δίνεται o κύκλος \(𝐶:\ (𝑥−1)^2+(𝑦−2)^2=4\) και η ευθεία \((𝜀):\ 3𝑥−4𝑦=8.\)
α) Να βρείτε το κέντρο \(𝛫\) του κύκλου \(𝐶\) και την ακτίνα του.
(Μονάδες 5)
β) Αν \(𝛫(1,2)\), να δείξετε ότι η απόσταση του κέντρου του κύκλου \(𝐶\) από την ευθεία \((𝜀)\) είναι \(𝑑(𝛫,𝜀)=\dfrac{13}{5}.\)
(Μονάδες 13)
γ) Να αιτιολογήσετε γιατί η ευθεία και ο κύκλος δεν έχουν κανένα κοινό σημείο.
(Μονάδες 7)
Απάντηση Θέματος: 17317
α) Ο κύκλος \(𝐶\) έχει κέντρο \(𝛫(1,2)\) και ακτίνα \(𝜌=2.\)
β) Έχουμε: \(𝑑(𝛫,𝜀)=\dfrac{|3−8−8|}{\sqrt{3^2+4^2}}=\dfrac{13}{\sqrt{25}}=\dfrac{13}{5}.\)
γ) Αφού \(𝑑(𝛫,𝜀)=\dfrac{13}{5}>2\), η απόσταση του κέντρου του κύκλου από την ευθεία είναι μεγαλύτερη από την ακτίνα. Άρα ευθεία και κύκλος δεν έχουν κανένα κοινό σημείο.
Θέμα: 18237
ΘΕΜΑ 4
Θεωρούμε τα σημεία \(Α(-1,2)\), \(Β(3,2)\), \(Γ(1,4)\).
α) Να αποδείξετε ότι ορίζουν τρίγωνο.
(Μονάδες 6)
β) Να βρείτε την εξίσωση της μεσοκαθέτου της πλευράς \(ΒΓ\).
(Μονάδες 7)
Έστω ότι η μεσοκάθετος της πλευράς \(ΒΓ\) είναι η ευθεία \(ε:y=x+1\).
γ) Να βρείτε σημείο \(Κ\) στην μεσοκάθετο της πλευράς \(ΒΓ\) που ισαπέχει από τα \(Α\), \(Β\).
(Μονάδες 7)
δ) Να βρείτε την εξίσωση του περιγεγραμμένου κύκλου του τριγώνου \(ΑΒΓ\).
(Μονάδες 5)
Απάντηση Θέματος: 18237
α) Είναι \(\overrightarrow{AB}=(4,0)\) και \(\overrightarrow{AΓ}=(2,2)\), και επειδή
$$\det(\overrightarrow{AB},\overrightarrow{ΑΓ})=\begin{vmatrix}4&0\\0&0\end{vmatrix}=8\neq0,$$
τα σημεία \(Α\), \(Β\), \(Γ\) δεν είναι συνευθειακά, οπότε ορίζουν τρίγωνο.
β) Η πλευρά \(ΒΓ\) έχει μέσο το σημείο \(Μ\left(\dfrac{3+1}{2},\dfrac{2+4}{2}\right)\), δηλαδή το \(Μ(2,3)\), και συντελεστή διεύθυνσης
$$λ_{BΓ}=\frac{4-2}{1-3}=\frac{2}{-2}=-1,$$
οπότε η μεσοκάθετος \((ε)\) της \(ΒΓ\) διέρχεται από το \(Μ\) και έχει συντελεστή διεύθυνσης \(λ=1\). Επομένως, η εξίσωσης της ευθείας \((ε)\) είναι
$$y-3=x-2\iff y=x+1.$$
γ) Έστω \(K(x,y)\) το σημείο της μεσοκάθετης που ισαπέχει από τα σημεία \(Α\), \(Β\). Με \(y=x+1\), έχουμε
\begin{align}&(KA)=(KB)\\ \iff&(KA)^2=(KB)^2\\ \iff&(x+1)^2+(x-1)^2=(x-3)^2+(x-1)^2\\ \iff&x^2+2x+1=x^2-6x+9\\ \iff&8x=8\\ \iff&x=1,\end{align}
οπότε \(y=2\). Άρα, \(K(1,2)\).
δ) Το σημείο \(Κ\), από τον τρόπο προσδιορισμού του, ισαπέχει από τις κορυφές \(Α\), \(Β\), \(Γ\) του τριγώνου, άρα είναι το περίκεντρό του. Σε ότι αφορά στην ακτίνα \(ρ\) του περιγεγραμμένου κύκλου, ισχύει
\begin{align}ρ&=(KA)\\ &=\sqrt{(-1-1)^2+(2-2)^2}\\ &=\sqrt{4}\\ &=2.\end{align}
Επομένως, ο περιγεγραμμένος κύκλος του τριγώνου \(ΑΒΓ\) έχει εξίσωση
$$(x-1)^2+(y-2)^2=4.$$
Θέμα: 18238
ΘΕΜΑ 2
Δίνονται τα σημεία \(A(1,3)\) και \(Β(-3,5).\)
α) Να βρείτε τις συντεταγμένες του μέσου \(Κ\) του τμήματος \(ΑΒ.\)
(Μονάδες 7)
β) Να αποδείξετε ότι \((ΚΑ)=\sqrt{5}.\)
(Μονάδες 8)
γ) Να βρείτε την εξίσωση του κύκλου που έχει διάμετρο το ευθύγραμμο τμήμα \(ΑΒ.\)
(Μονάδες 10)
Απάντηση Θέματος: 18238
α) Είναι
$$\begin{cases} x_K=\dfrac{x_A+x_B}{2}=\dfrac{1+(-3)}{2}=-1 \\ y_K=\dfrac{y_A+y_B}{2}=\dfrac{3+5}{2}=4\end{cases}$$
Οπότε: \(K(-1,4).\)
β) Είναι
$$\begin{align} (KA) &=\sqrt{(x_K-x_A)^2+(y_K-y_A)^2}\\ &=\sqrt{(-1-1)^2+(4-3)^2}\\ &=\sqrt{5}.\end{align}$$
γ) Ο ζητούμενος κύκλος έχει κέντρο το σημείο \(Κ(-1,4)\) και ακτίνα την απόσταση \((ΚΑ)=\sqrt{5}\), οπότε έχει εξίσωση: \((x+1)^2+(y-4)^2=5.\)
Θέμα: 18239
ΘΕΜΑ 2
Δίνεται το σημείο \(K(-3,1)\) και η ευθεία
$$ε: 4x-3y+5=0.$$
α) Να αποδείξετε ότι η απόσταση του σημείου \(Κ\) από την ευθεία \((ε)\) είναι ίση με \(2\).
(Μονάδες 6)
β) Να βρείτε την εξίσωση του κύκλου \(C\) που έχει κέντρο το σημείο \(Κ\) και εφάπτεται στην ευθεία \((ε)\).
(Μονάδες 9)
γ) Να σχεδιάσετε στο ίδιο ορθοκανονικό σύστημα αξόνων τον κύκλο \(C\) και την ευθεία \((ε)\).
(Μονάδες 10)
Απάντηση Θέματος: 18239
α) Είναι
\begin{align}d(K,ε)&=\frac{|4\cdot (-3)-3\cdot 1+5|}{\sqrt{4^2+3^2}}\\ &=\frac{|-10|}{\sqrt{25}}\\ &=\frac{10}{5}\\ &=2.\end{align}
β) Ο ζητούμενος κύκλος θα έχει ακτίνα \(ρ=d(Κ,ε)=2\), οπότε η εξίσωσή του θα είναι η
$$(x+3)^2+(y-1)^2=4.$$
γ) Η ευθεία \((ε)\) διέρχεται από τα σημεία \(Α(-2,-1)\) και \(Β(1,3)\), αφού οι συντεταγμένες τους επαληθεύουν την εξίσωσή της. Ο κύκλος \(C\) και η ευθεία \((ε)\) φαίνονται στο παρακάτω σχήμα.
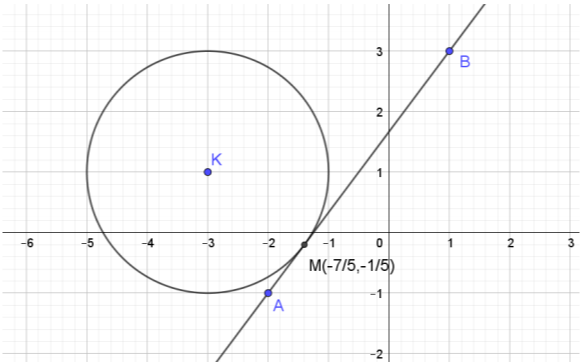
Θέμα: 18241
ΘΕΜΑ 2
Δίνεται ο κύκλος \(C\) με εξίσωση \(x^2+y^2=25\). Να σχεδιάσετε στο ίδιο ορθοκανονικό σύστημα συντεταγμένων:
α) Τον κύκλο \(C\).
(Μονάδες 9)
β) Τις εφαπτόμενες του \(C\) που διέρχονται από τα σημεία τομής του \(C\) με τον \(yy'\) και να γράψετε τις εξισώσεις τους.
(Μονάδες 8)
γ) Τις εφαπτόμενες του \(C\) που διέρχονται από τα σημεία τομής του \(C\) με τον \(xx'\) και να γράψετε τις εξισώσεις τους.
(Μονάδες 8)
Απάντηση Θέματος: 18241
α) Ο κύκλος \(C\), που φαίνεται στο παρακάτω σχήμα, έχει κέντρο το \(Ο(0,0)\) και ακτίνα \(ρ=5\). Τα σημεία τομής με τον άξονα \(xx'\) είναι τα σημεία \(Α(5,0)\) και \(Β(-5,0)\), ενώ τα σημεία τομής με τον άξονα \(yy'\) είναι τα σημεία \(Γ(0,5)\) και \(Δ(0,-5)\).
β) Αναζητούμε τις εφαπτόμενες του κύκλου στα σημεία \(Γ(0,5)\) και \(Δ(0,-5)\). Οι εφαπτόμενες αυτές είναι κάθετες στον \(yy'\), οπότε παράλληλες στον \(xx'\), και διέρχονται από τα σημεία \(Γ(0,5)\) και \(Δ(0,-5)\), άρα έχουν εξισώσεις \(y=5\) και \(y=-5\), αντίστοιχα. Είναι οι ευθείες \(ε_3\), \(ε_4\) που φαίνονται στο παρακάτω σχήμα.
γ) Αναζητούμε τις εφαπτόμενες του κύκλου στα σημεία \(Α(5,0)\) και \(Β(-5,0)\). Οι εφαπτόμενες αυτές είναι κάθετες στον \(xx'\), οπότε παράλληλες στον \(yy'\), και διέρχονται από τα σημεία \(Α(5,0)\) και \(Β(-5,0)\), άρα έχουν εξισώσεις \(x=5\) και \(x=-5\), αντίστοιχα. Είναι οι ευθείες \(ε_1\), \(ε_2\) που φαίνονται στο παρακάτω σχήμα.
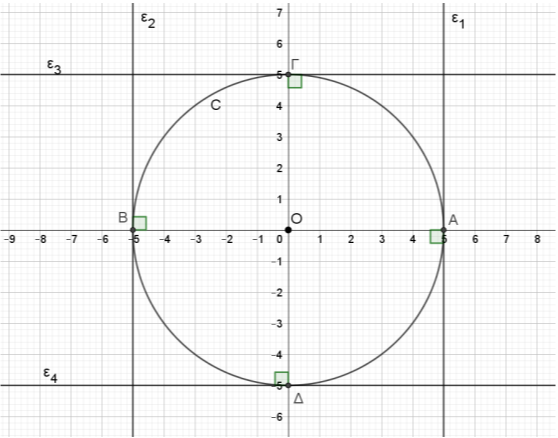
Θέμα: 18247
ΘΕΜΑ 4
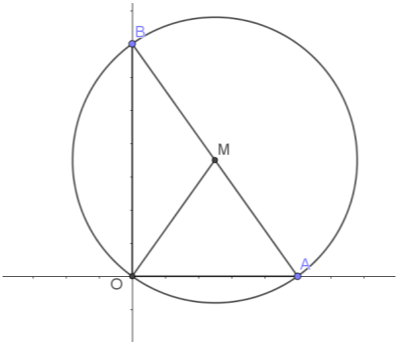
Δίνονται τα σημεία \(Ο(0,0)\), \(Α(α,0)\) και \(Β(0,β)\), όπου \(α,β >0\).
α) Να βρείτε συναρτήσει των \(α,β\)
i. τις συντεταγμένες του μέσου \(Μ\) του τμήματος \(ΑΒ\).
(Μονάδες 5)
ii. την απόσταση \((ΟΜ)\).
(Μονάδες 5)
β) Αν \((ΟΜ)=\dfrac{\sqrt{α^2+β^2}}{2}\), τότε:
i. να αποδείξετε ότι \((ΟΜ)=\dfrac{(ΑΒ)}{2}\).
(Μονάδες 5)
ii. να γράψετε την πρόταση της Ευκλείδειας Γεωμετρίας που έχει αποδειχθεί.
(Μονάδες 3)
γ) Να βρείτε την εξίσωση του περιγεγραμμένου κύκλου του τριγώνου \(ΟΑΒ\).
(Μονάδες 7)
Απάντηση Θέματος: 18247
α) i. Οι συντεταγμένες του μέσου \(Μ\) του τμήματος \(ΑΒ\) είναι \(Μ\left(\dfrac{α}{2},\dfrac{β}{2}\right)\).
ii. Η απόσταση \((ΟΜ)\) είναι
\begin{align}(OM)&=\sqrt{\left(\frac{α}{2}-0\right)^2+\left(\frac{β}{2}-0\right)^2}\\ &=\sqrt{\frac{α^2}{4}+\frac{β^2}{4}}\\ &=\sqrt{\frac{α^2+β^2}{4}}\\ &=\frac{\sqrt{α^2+β^2}}{2}.\end{align}
β) i. Είναι
\begin{align}(AB)&=\sqrt{(α-0)^2+(0-β)^2}\\ &=\sqrt{α^2+β^2}\\ &=2\cdot(OM),\end{align}
άρα \((ΟΜ)=\dfrac{(AB)}{2}\).
ii. Η πρόταση της Ευκλείδειας Γεωμετρίας που έχει αποδειχθεί είναι η εξής:
Σε κάθε ορθογώνιο τρίγωνο, η διάμεσος που αντιστοιχεί στην υποτείνουσα ισούται με το μισό της υποτείνουσας.
γ) Αφού
$$(OM)=\frac{(AB)}{2}=(AM)=(BM),$$
συμπεραίνουμε ότι το σημείο \(Μ\) ισαπέχει από τις κορυφές του τριγώνου \(ΟΑΒ\) και επομένως είναι το κέντρο του ζητούμενου περιγεγραμμένου κύκλου. Επίσης, η ακτίνα του ζητούμενου κύκλου είναι η \((ΟΜ)=\dfrac{\sqrt{α^2+β^2}}{2}\). Συνεπώς, ο ζητούμενος κύκλος έχει εξίσωση
$$\left(x-\frac{α}{2}\right)^2+\left(y-\frac{β}{2}\right)^2=\frac{α^2+β^2}{4}.$$
Θέμα: 18415
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$(x-3λ)^2+(y+2λ)^2=1\quad(1)$$
όπου \(λ\in\mathbb{R}\), και η ευθεία
$$ε:2x+3y=0.$$
α) Να αποδείξετε ότι για κάθε \(λ\in\mathbb{R}\) τα κέντρα των κύκλων που προκύπτουν από την \((1)\) ανήκουν στην ευθεία \(ε\).
(Μονάδες 6)
β) Να βρείτε τις εξισώσεις των ευθειών \(ε_1\), \(ε_2\) που απέχουν μεταξύ τους \(2\) μονάδες και έχουν μεσοπαράλληλο την ευθεία \(ε\).
(Μονάδες 7)
γ) Να αποδείξετε ότι όλοι οι κύκλοι που προκύπτουν από την \((1)\) εφάπτονται σε δύο σταθερές ευθείες.
(Μονάδες 6)
δ) Να βρείτε το εμβαδόν ενός τετραγώνου του οποίου δύο απέναντι πλευρές ανήκουν στις ευθείες \(ε_1\) και \(ε_2\), αντίστοιχα.
(Μονάδες 6)
Απάντηση Θέματος: 18415
α) Η \((1)\) για κάθε \(λ\in\mathbb{R}\) παριστάνει κύκλο με κέντρο \(Κ(3λ,-2λ)\) που ανήκει στην ευθεία \(ε\), αφού
$$2\cdot 3λ+3\cdot(-2λ)=6λ-6λ=0.$$
β) Αν \(Μ(x,y)\) τυχαίο σημείο μιας εκ των ευθειών \(ε_1\), \(ε_2\), τότε
\begin{align}&d(M,ε)=1\\ \iff&\frac{|2x+3y|}{\sqrt{2^2+3^2}}=1\\ \iff&|2x+3y|=\sqrt{13},\end{align}
οπότε \(2x+3y=\sqrt{13}\) ή \(2x+3y=-\sqrt{13}\), που είναι οι ζητούμενες εξισώσεις των ευθειών \(ε_1\), \(ε_2\).
γ) Αφού τα κέντρα \(Κ(3λ,-2λ)\) όλων των κύκλων που προκύπτουν από την \((1)\) ανήκουν στην \(ε\), δηλαδή στη μεσοπαράλληλο των \(ε_1\), \(ε_2\), έχουμε ότι
$$d(K,ε_1)=d(K,ε_2)=1=ρ.$$
Συνεπώς όλοι οι κύκλοι που προκύπτουν από την \((1)\) αφάπτονται στις ευθείες \(ε_1\), \(ε_2\).
δ) Ένα τετράγωνο του οποίου οι δύο απέναντι πλευρές ανήκουν στις ευθείες \(ε_1\), \(ε_2\) θα έχει μήκος πλευράς ίσο με την απόσταση των \(ε_1\), \(ε_2\), δηλαδή \(2\). Συνεπώς το εμβαδόν του θα είναι ίσο με \(4\).
Θέμα: 18416
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x(x-4)+y(y-2)=2(x+y-4)\quad(1)$$
α) Να δείξετε ότι η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο \(Κ(3,2)\) και ακτίνα \(ρ=\sqrt{5}\).
(Μονάδες 6)
β) Δίνονται τα σημεία \(Α(4,4)\) και \(Β(2,0)\).
i. Να δείξετε ότι τα σημεία \(Α\) και \(Β\) είναι αντιδιαμετρικά σημεία του κύκλου.
(Μονάδες 4)
ii. Να βρείτε τις εξισώσεις των εφαπτόμενων του κύκλου οι οποίες είναι παράλληλες στη διάμετρο \(ΑΒ\).
(Μονάδες 9)
γ) Να βρείτε την τιμή της παραμέτρου \(λ\) ώστε η ευθεία \((η)\) με εξίσωση \(y=λx+4\) να τέμνει τον παραπάνω κύκλο σε δύο σημεία \(Γ\) και \(Δ\) ώστε \((ΓΔ)=\sqrt{20}\).
(Μονάδες 6)
Απάντηση Θέματος: 18416
α) Η δοθείσα γράφεται:
\begin{align}&x^2-4x+y^2-2y=2x+2y-8\\ \iff&x^2-6x+y^2-4y=-8\\ \iff&x^2-2\cdot 3\cdot x+3^2+y^2-2\cdot 2\cdot y+2^2=3^2+2^2-8\\ \iff&(x-3)^2+(y-2)^2=5\quad (2)\end{align}
Άρα η εξίσωση παριστάνει κύκλο με κέντρο \(Κ(3,2)\) και ακτίνα \(ρ=\sqrt{5}\).
β) i. Η \((2)\) για \(x=4\) και \(y=4\) δίνει
$$(4-3)^2+(4-2)^2=5\iff 1^2+2^2=5$$
που ισχύει. Επίσης η \((2)\) για \(x=2\) και \(y=0\) δίνει
$$(2-3)^2+(0-2)^2=5\iff 1^2+2^2=5$$
που ισχύει. Συνεπώς τα σημεία \(Α\) και \(Β\) είναι πάνω στον κύκλο. Για να είναι αντιδιαμετρικά αρκεί το κέντρο \(Κ\) να είναι το μέσο του τμήματος \(ΑΒ\). Πράγματι,
\begin{align}&x_K=\frac{x_A+x_B}{2}\\ \iff&3=\frac{4+2}{2}\\ \iff&3=3\end{align}
και
\begin{align}&y_K=\frac{y_A+y_B}{2}\\ \iff&2=\frac{4+0}{2}\\ \iff&2=2\end{align}
που ισχύουν.
ii. Ο συντελεστής διεύθυνσης της διαμέτρου \(ΑΒ\) είναι \(λ=\dfrac{0-4}{2-4}=2\). Άρα και οι ζητούμενες εφαπτόμενες έχουν κλίση \(2\). Έστω
$$ε:y=2x+β\iff 2x-y+β=0$$
η εξίσωση της εφαπτόμενης του κύκλου. Για να εφάπτεται στον κύκλο αρκεί
\begin{align}&d(K,ε)=ρ\\ \iff&\frac{|2\cdot 3-2+β|}{\sqrt{2^2+(-1)^2}}=\sqrt{5}\\ \iff&|β+4|=5\\ \iff&β+4=\pm 5\\ \iff&β=1\text{ ή }β=-9.\end{align}
Επομένως οι εφαπτόμενες του κύκλου οι οποίες είναι παράλληλες στη διάμετρο \(ΑΒ\) έχουν εξισώσεις \(ε_1: y=2x+1\) και \(ε_2: y=2x-9\).
γ) Ισχύει
$$(ΓΔ)=\sqrt{20}=2\sqrt{5}=2ρ.$$
Αυτό σημαίνει ότι τα σημεία \(Γ\) και \(Δ\) είναι αντιδιαμετρικά, δηλαδή η ευθεία \((η)\) πρέπει να διέρχεται από το κέντρο \(Κ\) του κύκλου. Άρα αντικαθιστώντας στην εξίσωση της \((η)\) τις συντεταγμένες του κέντρου \(x=3\) και \(y=2\) έχουμε
$$2=3λ+4\iff λ=-\frac{2}{3}.$$
Θέμα: 18567
ΘΕΜΑ 4
Δίνεται ο κύκλος \(C:x^2+y^2=4\) και το σημείο \(Α(2\sqrt{2},0)\).
α) i. Να αποδείξετε ότι το σημείο \(Α\) είναι εξωτερικό του κύκλου \(C\).
(Μονάδες 5)
ii. Να βρείτε τις εξισώσεις των εφαπτομένων του κύκλου \(C\) που διέρχονται από το σημείο \(Α\) και να αποδείξετε ότι είναι μεταξύ τους κάθετες.
(Μονάδες 12)
β) Αν \(Β\), \(Γ\) τα σημεία επαφής του κύκλου \(C\) με τις εφαπτόμενες ευθείες από το σημείο \(Α\), να υπολογίσετε το εμβαδό του τετραπλεύρου \(ΑΒΟΓ\).
(Μονάδες 8)
Απάντηση Θέματος: 18567

α)
-
Το σημείο \(Α(2\sqrt{2},0)\) είναι εξωτερικό του κύκλου \(C\) γιατί είναι σημείο του θετικού ημιάξονα \(Ox\) με \((ΟΑ)=2\sqrt{2} > 2\).
-
Οι ευθείες που διέρχονται από το σημείο \(Α(2\sqrt{2},0)\) είναι:
\(\bullet\) Η κατακόρυφη \(x=2\sqrt{2}\) που δεν είναι εφαπτομένη του κύκλου \(C\) γιατί \(d(O,ε)=2\sqrt{2}\).
\(\bullet\) Οι ευθείες \((ε)\) με εξίσωση
$$y-0=λ(x-2\sqrt{2})$$ $$\iff λx-y-2λ\sqrt{2}=0,\ λ\in\mathbb{R}.$$
Η \((ε)\) είναι εφαπτομένη του \(C\) αν και μόνο αν η απόσταση του κέντρου του, \(Ο\), από αυτή ισούται με την ακτίνα του κύκλου. Δηλαδή
\begin{align}&d(O,ε)=ρ\\ \iff&\frac{|λ\cdot 0-0-2λ\sqrt{2}|}{\sqrt{λ^2+1}}=2\\ \iff&2\sqrt{2}|λ|=2\sqrt{λ^2+1}\\ \iff&8λ^2=4λ^2+4\\ \iff&4λ^2-4=0\\ \iff&λ^2=1\\ \iff&λ=\pm1.\end{align}
Για \(λ=1\) είναι
$$ε_1:y=x-2\sqrt{2}$$
και για \(λ=-1\) έχουμε
$$ε_2:y=-x+2\sqrt{2}.$$
Παρατηρούμε ότι οι συντελεστές διεύθυνσης \(λ_1\) και \(λ_2\) των ευθειών \((ε_1)\) και \((ε_2)\) είναι \(1\) και \(-1\), αντίστοιχα, και \(λ_1\cdot λ_2=-1\). Άρα οι εφαπτόμενες ευθείες \((ε_1)\) και \((ε_2)\) του κύκλου από το σημείο \(Α\) είναι μεταξύ τους κάθετες.
β) Αν \(Β\), \(Γ\) τα σημεία επαφής των εφαπτόμενων ευθειών \((ε_1)\) και \((ε_2)\) με τον κύκλο \(C\), τότε οι ακτίνες του κύκλου στα σημεία αυτά είναι κάθετες στις αντίστοιχες εφαπτόμενες. Δηλαδή το τετράπλευρο \(ΑΒΟΓ\) έχει \(3\) ορθές γωνίες, οπότε είναι ορθογώνιο παραλληλόγραμμο. Επειδή \(ΟΑ=ΟΒ=2\) ως ακτίνες του κύκλου, είναι επιπλέον και ρόμβος. Επομένως το \(ΑΒΟΓ\) είναι τετράγωνο με πλευρά ίση με την ακτίνα του κύκλου, δηλαδή \(2\).
Συνεπώς \((ΑΒΟΓ)=2^2=4\).
Θέμα: 18569
ΘΕΜΑ 4
Δίνεται ο κύκλος \(C: x^2+y^2=1\).
α) Αν \(Α\) και \(Α'\) είναι τα σημεία τομής του κύκλου \(C\) με τους ημιάξονες \(Ox\) και \(Οx'\), αντίστοιχα, τότε:
i. Να αποδείξετε ότι οι συντεταγμένες των σημείων \(Α\) και \(Α'\) είναι \(Α(1,0)\) και \(Α'(-1,0)\).
(Μονάδες 5)
ii. Να βρείτε την εξίσωση της ευθείας \((ε)\) που διέρχεται από το \(Α\) και σχηματίζει με τον άξονα \(x'x\) γωνία \(150^ο\).
(Μονάδες 6)
β) Αν η ευθεία \((ε)\) τέμνει τον κύκλο \(C\) και στο σημείο \(Β\), να αποδείξετε ότι η χορδή \(ΑΒ\) έχει μήκος \(\sqrt{3}\).
(Μονάδες 8)
γ) Αν η ευθεία \((ε)\) έχει εξίσωση \(y=-\dfrac{\sqrt{3}}{3}(x-1)\), να βρείτε την εξίσωση της ευθείας \((ζ)\) που διέρχεται από τα σημεία \(Α'\) και \(Β\).
(Μονάδες 6)
Απάντηση Θέματος: 18569
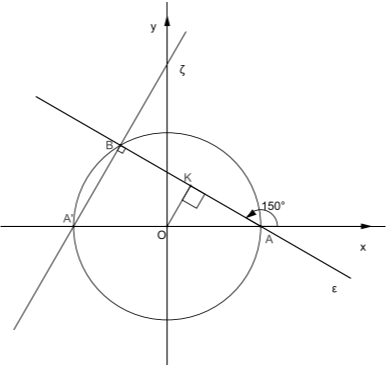
α) i. Τα σημεία τομής του κύκλου \(C\) με τους ημιάξονες \(Ox\) και \(Ox'\) έχουν τεταγμένη μηδέν. Επομένως, για \(y=0\) έχουμε
$$x^2=1\iff x=\pm1.$$
Άρα \(Α'(-1,0)\) και \(Α(1,0)\).
ii. Ο συντελεστής διεύθυνσης της ευθείας \((ε)\) που διέρχεται από το σημείο \(Α(1,0)\) είναι
$$λ_ε=εφ150^ο=-\frac{\sqrt{3}}{3}.$$
Οπότε η εξίσωση της \((ε)\) είναι
$$y-0=-\frac{\sqrt{3}}{3}(x-1)\iff y=-\frac{\sqrt{3}}{3}(x-1).$$
β) Αν \(ΟΚ\) το απόστημα της χορδής \(ΑΒ\), τότε
\begin{align}OK&=d(O,ε)\\ &=\dfrac{|-\dfrac{\sqrt{3}}{3}\cdot 0-0+\dfrac{\sqrt{3}}{3}|}{\sqrt{\left(-\dfrac{\sqrt{3}}{3}\right)^2+1^2}}\\ &=\frac{|\dfrac{\sqrt{3}}{3}|}{\sqrt{\dfrac{12}{9}}}\\ &=\dfrac{\dfrac{\sqrt{3}}{3}}{2\dfrac{\sqrt{3}}{3}}\\ &=\dfrac{1}{2}.\end{align}
Αν \(ΑΚ=μ=\dfrac{AB}{2}\), με Πυθαγόρειο θεώρημα στο τρίγωνο \(ΟΑΚ\) έχουμε
\begin{align}&OK^2+μ^2=ΟΑ^2\\ \iff&μ^2=1-\frac{1}{4}\\ \iff&μ^2=\frac{3}{4}\\ \iff&μ=\frac{\sqrt{3}}{2}.\end{align}
Άρα
$$ΑΒ=2μ=\sqrt{3}.$$
γ) Η γωνία \(\widehat{A'BA}\) είναι εγγεγραμμένη που βαίνει σε ημικύκλιο, άρα \(Α'Β\perp BA\), δηλαδή \(ζ\perp ε\). Οπότε
$$λ_ζ=-\frac{1}{λ_ε}=\frac{3}{\sqrt{3}}=\sqrt{3}$$
και η εξίσωση της \((ζ)\) είναι
$$y-0=\sqrt{3}(x+1)\iff y=\sqrt{3}(x+1).$$
Θέμα: 18700
ΘΕΜΑ 2
Δίνεται κύκλος \(C\) με κέντρο την αρχή των αξόνων και ακτίνα \(5\).
α) Να γράψετε την εξίσωση του κύκλου \(C\) και να τον σχεδιάσετε σε ορθοκανονικό σύστημα αξόνων.
(Μονάδες 10)
β) Δίνεται το σημείο \(Α(3,-4)\).
i. Να αποδείξετε ότι το σημείο \(Α\) ανήκει στον κύκλο \(C\).
(Μονάδες 5)
ii. Να βρείτε την εξίσωση της εφαπτομένης του κύκλου \(C\) στο σημείο \(Α\).
(Μονάδες 10)
Απάντηση Θέματος: 18700
α) Η εξίσωση του κύκλου με κέντρο την αρχή των αξόνων, δηλαδή το \((0,0)\), και ακτίνα \(5\) είναι
$$C: x^2+y^2=25.$$
Σε ορθοκανονικό σύστημα αξόνων και με τη βοήθεια του διαβήτη κατασκευάζουμε κύκλο με κέντρο το \((0,0)\) και ακτίνα ίση με την απόσταση του \(Ο\) από το σημείο \((5,0)\). Προκύπτει το παρακάτω σχήμα.
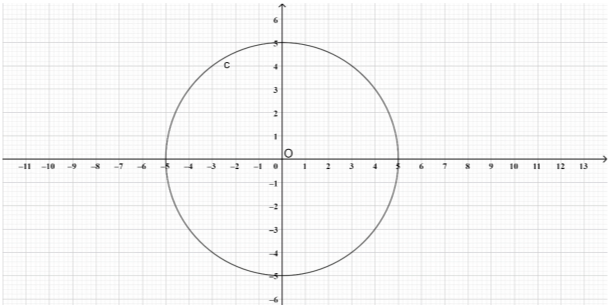
β) i. To σημείο \(Α(3,-4)\) επαληθεύει την εξίσωση του κύκλου \(C\), δηλαδή
$$3^2+(-4)^2=9+16=25.$$
Επίσης, και από το σχήμα που κάναμε στο (α) ερώτημα φαίνεται ότι το σημείο \(Α(3,-4)\) ανήκει στον κύκλο \(C\).
ii. Η εξίσωση εφαπτομένης στο σημείο \(Α(x_1,y_1)\) του κύκλου της μορφής \(x^2+y^2=ρ^2\) δίνεται από τον τύπο \(x_1\cdot x+y_1\cdot y=ρ^2\). Άρα, η εξίσωση εφαπτομένης στο \(Α(3,-4)\) του κύκλου \(C\) είναι
$$ε:3x-4y=25.$$
Θέμα: 19039
ΘΕΜΑ 2
Δίνεται η εξίσωση:
$$(x-1)(x+3)+(y+1)(y-3)=-4\quad(1)$$
α) Να αποδείξετε ότι η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο \(Κ(-1,1)\) και ακτίνα \(R=2\).
(Μονάδες 9)
β) i. Να βρείτε τα σημεία \(Α\) και \(Β\) του κύκλου \((Κ,R)\) τα οποία έχουν τετμημένη ίση με \(-1\).
(Μονάδες 8)
ii. Να αποδείξετε ότι τα σημεία \(Α\) και \(Β\) είναι αντιδιαμετρικά.
(Μονάδες 8)
Απάντηση Θέματος: 19039
α) Η εξίσωση \((1)\) γράφεται διαδοχικά:
\begin{align}&(x-1)(x+3)+(y+1)(y-3)=-4\\ \iff&(x^2+3x-x-3)+(y^2-3y+y-3)=-4\\ \iff&x^2+2x+y^2-2y=2\\ \iff&(x^2+2x+1)+(y^2-2y+1)=4\\ \iff&(x+1)^2+(y-1)^2=2^2\quad(2)\end{align}
Άρα, η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο \(Κ(-1,1)\) και ακτίνα \(R=2\).
β) i. Για \(x=-1\), η εξίσωση \((2)\) γίνεται
\begin{align}&(-1+1)^2+(y-1)^2=2^2\\ \iff&(y-1)^2=4\\ \iff&y-1=\pm2\\ \iff&y=3\text{ ή }y=-1.\end{align}
Επομένως, τα ζητούμενα σημεία είναι \(Α(-1,-1)\) και \(Β(-1,3)\).
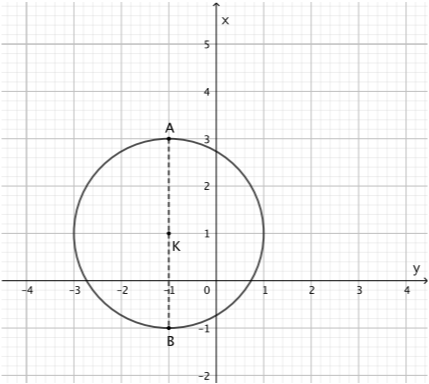
ii. Τα σημεία \(Α\) και \(Β\) βρίσκονται στην ευθεία \(x=-1\), η οποία διέρχεται από το κέντρο \(Κ\) του κύκλου. Επομένως, τα σημεία \(Α\) και \(Β\) είναι αντιδιαμετρικά σημεία του κύκλου.
Θέμα: 20091
ΘΕΜΑ 4
Τα σημεία \(Α(-7.-1)\) και \(Β(3,-5)\) είναι σημεία ενός κύκλου \(C\) κέντρου \(Κ\). Το σημείο \(Μ\) είναι το μέσο της χορδής \(ΑΒ\) και μια ευθεία \((ε)\) διέρχεται από τα σημεία \(Κ\) και \(Μ\).
α) Να βρείτε:
i. Τις συντεταγμένες του σημείου \(Μ\).
(Μονάδες 4)
ii. Την εξίσωση της ευθείας \(ΚΜ\).
(Μονάδες 8)
β) Αν από το κέντρο \(Κ\) του κύκλου διέρχεται η ευθεία \(δ:x+y=-12\), τότε:
i. Να βρείτε τις συντεταγμένες του σημείου \(Κ\).
(Μονάδες 7)
ii. Να βρείτε την εξίσωση του κύκλου \(C\).
(Μονάδες 6)
Απάντηση Θέματος: 20091
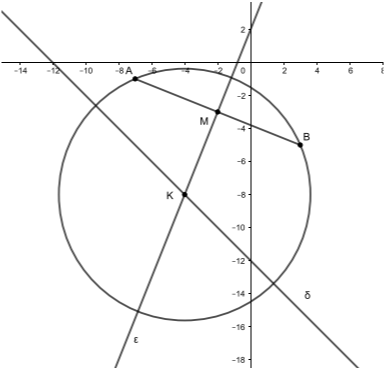
α) i. Το μέσο \(Μ\) του τμήματος \(ΑΒ\) έχει συντεταγμένες \(Μ\left(\dfrac{-7+3}{2},\dfrac{-1-5}{2}\right)=(-2,3)\).
ii. Το τμήμα \(ΚΜ\) ενώνει το κέντρο του κύκλου με το μέσο \(Μ\) της χορδής \(ΑΒ\), οπότε είναι το απόστημα της χορδής και \(ΚΜ\perp ΑΒ\). Οπότε \(λ_{ΑΒ}\cdot λ_{ΚΜ}=-1\). Είναι
$$λ_{ΑΒ}=\frac{-5+1}{3+7}=-\frac{2}{5},$$
επομένως \(λ_{ΚΜ}=\dfrac{5}{2}\). Η εξίσωση της ευθείας \(ΚΜ\) είναι
\begin{align}&y-y_M=\frac{5}{2}(x-x_M)\\ \iff&y+3=\frac{5}{2}(x+2)\\ \iff&2y+6=5x+10\\ \iff&5x-2y+4=0.\end{align}
β) i. Το κέντρο \(Κ\) του κύκλου ανήκει στην ευθεία \((δ)\) και στην ευθεία \(ΚΜ\). Άρα η τομή των δύο ευθειών, δηλαδή η λύση του συστήματος των δύο εξισώσεών τους, θα είναι οι συντεταγμένες του σημείου \(Κ\). Έχουμε:
\begin{align}&\begin{cases}5x-2y=-4\\x+y=-12\end{cases}\\ \iff&\begin{cases}5x-2y=-4\\2x+2y=-24\end{cases}\\ \iff&\begin{cases}7x=-28\\x+y=-12\end{cases}\\ \iff&\begin{cases}x=-4\\y=-8\end{cases}\end{align}
Άρα \(Κ(-4,-8)\).
ii. Αρκεί να βρούμε την ακτίνα του κύκλου που είναι το μήκος του τμήματος \(ΚΑ\). Είναι
\begin{align}(KA)&=\sqrt{(-4+7)^2+(-8+1)^2}\\ &=\sqrt{9+49}\\ &=\sqrt{58}.\end{align}
Επομένως, η εξίσωση του κύκλου είναι
$$C:(x+4)^2+(y+8)^2=58.$$
Θέμα: 20229
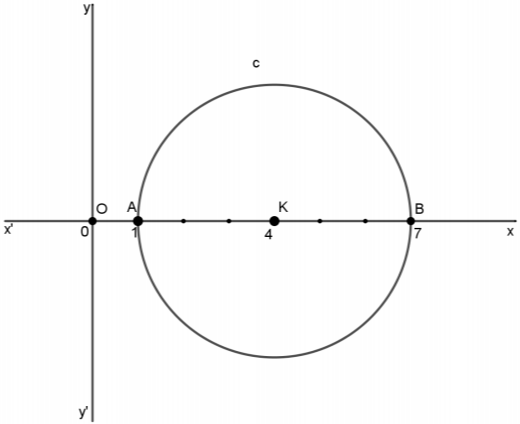
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x^2+y^2-(λ + 8)x+λy+7=0\quad(1)$$
με \(λ\in\mathbb{R}\).
α) Να αποδείξετε ότι για κάθε \(λ\in\mathbb{R}\) η εξίσωση \((1)\) παριστάνει κύκλο, του οποίου να βρεθεί το κέντρο και η ακτίνα.
(Μονάδες 6)
β) Να βρείτε την εξίσωση της γραμμής πάνω στην οποία κινούνται τα κέντρα των κύκλων αυτών.
(Μονάδες 7)
γ) Να αποδείξετε ότι για κάθε \(λ\in\mathbb{R}\), όλοι οι παραπάνω κύκλοι διέρχονται από δύο σταθερά σημεία, τα οποία και να βρεθούν.
(Μονάδες 7)
δ) Θεωρούμε τον κύκλο που ορίζεται από την \((1)\) για \(λ=0\). Να βρεθούν τα σημεία του κύκλου αυτού, που απέχουν από την αρχή των αξόνων την ελάχιστη και την μέγιστη απόσταση, αντίστοιχα.
(Μονάδες 5)
Απάντηση Θέματος: 20229
α) Έχουμε την εξίσωση
$$x^2+y^2-(λ+8)x+λy+7=0\quad(1),$$
με \(λ\in\mathbb{R}\), για την οποία \(Α=-(λ+8)\), \(Β=λ\) και \(Γ=7\), οπότε
\begin{align}Α^2+Β^2-4Γ&=[-(λ+8)]^2+λ^2-4\cdot 7\\ &=(λ+8)^2+λ^2-28\\ &=λ^2+16λ+64+λ^2-28\\ &=2λ^2+16λ+36\\ &=2(λ^2+8λ+18) > 0,\end{align}
για κάθε \(λ\in\mathbb{R}\), εφόσον η διακρίνουσα του τριωνύμου είναι \(Δ=-8 < 0\). Άρα η εξίσωση \((1)\) παριστάνει κύκλο για κάθε \(λ\in\mathbb{R}\). Επίσης, το κέντρο \(K\) των κύκλων που ορίζονται από την \((1)\) είναι το
\begin{align}\left(-\frac{Α}{2},-\frac{Β}{2}\right)&=\left(-\frac{-(λ+8)}{2},-\frac{λ}{2}\right)\\ &=\left(\frac{λ+8}{2},-\frac{λ}{2}\right),\ λ\in\mathbb{R}\end{align}
και ακτίνα η
\begin{align}ρ&=\frac{1}{2}\sqrt{Α^2+Β^2-4Γ}\\ &=\frac{1}{2}\sqrt{2(λ^2+8λ+18)},\ λ\in\mathbb{R}.\end{align}
β) Λόγω του ερωτήματος (α), τα κέντρα των κύκλων που εκφράζει η εξίσωση \((1)\) είναι τα \(Κ\left(\dfrac{λ+8}{2},-\dfrac{λ}{2}\right)\), \(λ\in\mathbb{R}\). Αν \(Κ(x, y)\), τότε
\begin{align}&\begin{cases}x=\frac{λ+8}{2}\\y=-\frac{λ}{2}\\λ\in\mathbb{R}\end{cases}\\ \iff&\begin{cases}x=\frac{-2y+8}{2}\\λ=-2y\end{cases}\\ \iff&\begin{cases}x=-y+4\\λ=-2y\\λ\in\mathbb{R}\end{cases}\\ \iff&\begin{cases}x+y-4=0\\λ=-2y\\λ\in\mathbb{R}\end{cases}\end{align}
Άρα τα κέντρα των κύκλων της εξίσωσης \((1)\), κινούνται στην ευθεία
$$ε: x+y−4=0.$$
γ) Η εξίσωση \((1)\) για κάθε \(λ\in\mathbb{R}\) γράφεται
\begin{align}&x^2+y^2-λx-8x+λy+7=0\\ \iff&(x^2+y^2-8x+7)+λ(y-x)=0,\end{align}
οπότε:
\begin{align}&\begin{cases}y-x=0\\x^2+y^2-8x+7=0\end{cases}\\ \iff&\begin{cases}y=x\\x^2+x^2-8x+7=0\end{cases}\\ \iff&\begin{cases}y=x\\2x^2-8x+7=0\end{cases}\\ \iff&\begin{cases}y=x\\x=2\pm\frac{\sqrt{2}}{2}\end{cases}\end{align}
Επομένως για κάθε \(λ\in\mathbb{R}\), όλοι οι κύκλοι \((1)\) διέρχονται από τα σταθερά σημεία \(Μ\left(2-\dfrac{\sqrt{2}}{2},2-\dfrac{\sqrt{2}}{2}\right)\) και \(Ν\left(2+\dfrac{\sqrt{2}}{2},2+\dfrac{\sqrt{2}}{2}\right)\).
δ) Λόγω του ερωτήματος (α), για \(λ=0\) η εξίσωση \((1)\) εκφράζει κύκλο με κέντρο το \(Κ(4,0)\) και ακτίνα \(ρ=3\). Ο κύκλος αυτός φαίνεται στο παρακάτω σχήμα. Τα σημεία του κύκλου που απέχουν την ελάχιστη και μέγιστη απόσταση από την αρχή των αξόνων βρίσκονται πάνω στην \(ΟΚ\). Οπότε το σημείο του που απέχει τη μικρότερη απόσταση από το \(Ο(0,0)\) είναι το \(Α(1,0)\), και το σημείο του που απέχει τη μεγαλύτερη απόσταση είναι το \(Β(7,0)\).
Θέμα: 20890
ΘΕΜΑ 2
Δίνεται το τρίγωνο \(ΑΒΓ\) με κορυφές τα σημεία \(A(3,-3)\), \(B(2,-8)\) και \(Γ(7,-3)\). Να βρείτε:
α) Την εξίσωση της πλευράς \(ΒΓ\).
(Μονάδες 10)
β) Την εξίσωση του κύκλου που έχει κέντρο το \(Α\) και εφάπτεται στην πλευρά \(ΒΓ\).
(Μονάδες 15)
Απάντηση Θέματος: 20890
α) Η \(ΒΓ\) έχει εξίσωση
\begin{align}&y-y_Γ=\frac{y_B-y_Γ}{x_B-x_Γ}(x-x_Γ)\\ \iff&y+3=\frac{-8+3}{2-7}(x-7)\\ \iff&y+3=\frac{-5}{-5}(x-7)\\ \iff&y+3=x-7\\ \iff&x-y-10=0.\end{align}
β) Η ακτίνα του ζητούμενου κύκλου είναι
\begin{align}ρ&=d(Α,ΒΓ)\\ &=\frac{|1\cdot 3-1\cdot(-3)-10|}{\sqrt{1^2+(-1)^2}}\\ &=\frac{|-4|}{\sqrt{2}}\\ &=\frac{4}{\sqrt{2}}\\ &=2\sqrt{2},\end{align}
οπότε η ζητούμενη εξίσωση είναι
\begin{align}&(x-x_A)^2+(y-y_A)^2=ρ^2\\ \iff&(x-3)^2+(y+3)^2=(2\sqrt{2})^2\\ \iff&(x-3)^2+(y+3)^2=8.\end{align}
Θέμα: 21154
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x^2+y^2-4αx-4αy=0\quad(1)$$
όπου \(α\) είναι πραγματικός αριθμός.
α) Να βρείτε τις τιμές του \(α\) για τις οποίες η εξίσωση \((1)\) παριστάνει κύκλο.
(Μονάδες 8)
β) Να προσδιορίσετε το κέντρο \(Κ\) και την ακτίνα \(R\) των κύκλων ως συνάρτηση του \(α\).
(Μονάδες 6)
γ) Να βρείτε το γεωμετρικό τόπο των κέντρων των κύκλων για τις διάφορες τιμές του \(α\) του ερωτήματος (α).
(Μονάδες 5)
δ) Να εξετάσετε αν υπάρχει τιμή του \(α\) ώστε ο αντίστοιχος κύκλος που ορίζεται από την εξίσωση \((1)\) να εφάπτεται στον άξονα \(x'x\).
(Μονάδες 6)
Απάντηση Θέματος: 21154
α) Η εξίσωση \((1)\) είναι της μορφής
$$x^2+y^2+Ax+By+Γ=0$$
με \(Α=-4α\), \(Β=-4α\) και \(Γ=0\). Για να παριστάνει κύκλο θα πρέπει \(Α^2+Β^2-4Γ>0\). Είναι
$$A^2+B^2-4Γ=16α^2+16α^2=32α^2,$$
επομένως θα πρέπει \(α^2>0\). Η τελευταία σχέση ικανοποιείται αν και μόνο αν \(α\neq 0\).
β) Τα κέντρα των κύκλων που παριστάνει η εξίσωση \((1)\) για \(α\neq0\) είναι
$$K\left(-\frac{A}{2},-\frac{B}{2}\right)=(2α,2α)$$
και η ακτίνα
\begin{align}R&=\frac{\sqrt{A^2+B^2-4Γ}}{2}\\ &=\frac{\sqrt{32α^2}}{2}\\ &=\frac{4\sqrt{2}|α|}{2}\\ &=2\sqrt{2}|α|.\end{align}
γ) Για τα κέντρα των κύκλων έχουμε:
$$\begin{cases}x=2α\\y=2α\\α\neq 0\end{cases}$$
Επομένως, τα κέντρα των κύκλων κινούνται πάνω στην ευθεία \(y=x\) με εξαίρεση το σημείο \(Ο(0,0)\), αφού είναι \(x\neq 0\) και \(y\neq 0\).
δ) Για να εφάπτεται κάποιος από τους κύκλους που ορίζονται από την εξίσωση \((1)\) στον άξονα \(x'x\), θα πρέπει να ισχύει \(|y_K|=R\). Έχουμε διαδοχικά
\begin{align}&|2α|=2\sqrt{2}|α|\\ \iff&|α|=\sqrt{2}|α|\\ \iff&|α|(1-\sqrt{2})=0\\ \iff&α=0.\end{align}
Όμως \(α\neq 0\), οπότε δεν υπάρχει τιμή του \(α\) ώστε ο αντίστοιχος κύκλος που ορίζεται από την εξίσωση \((1)\) να εφάπτεται στον άξονα \(x'x\).
Θέμα: 21159
ΘΕΜΑ 4
Δίνονται τα σημεία \(Α(α,0)\) και \(Β(0,β)\) με \(α,β > 0\) και \(α+β=10\).
α) Να αποδείξετε ότι η εξίσωση των κύκλων με διάμετρο την \(ΑΒ\), για κάθε τιμή των \(α\) και \(β\), είναι \(x^2+y^2-αx-(10-α)y=0\).
(Μονάδες 8)
β) Να αποδείξετε ότι όλοι οι κύκλοι με διάμετρο την \(ΑΒ\), για τις διάφορες τιμές των \(α\) και \(β\), διέρχονται από δύο σταθερά σημεία, την αρχή \(Ο\) των αξόνων και ένα σημείο \(Ρ\) του οποίου να βρείτε τις συντεταγμένες.
(Μονάδες 9)
γ) Να βρείτε τον γεωμετρικό τόπο των κέντρων όλων των κύκλων με διάμετρο την \(ΑΒ\) για τις διάφορες τιμές των \(α\) και \(β\).
(Μονάδες 8)
Απάντηση Θέματος: 21159
α) Το κέντρο των κύκλων με διάμετρο την \(ΑΒ\) είναι το μέσο της \(Μ\), επομένως
$$M\left(\frac{α+0}{2},\frac{β+0}{2}\right)\iff M\left(\frac{α}{2},\frac{β}{2}\right)$$
και η ακτίνα τους είναι
$$ρ=\frac{AB}{2}=\frac{\sqrt{(0-α)^2+(β-0)^2}}{2}=\frac{\sqrt{α^2+β^2}}{2}.$$
Επομένως η εξίσωση των κύκλων είναι:
\begin{align}&\left(x-\frac{α}{2}\right)^2+\left(y-\frac{β}{2}\right)^2=\left(\frac{\sqrt{α^2+β^2}}{2}\right)^2\\ \iff&x^2-2x\frac{α}{2}+\frac{α^2}{4}+y^2-2y\frac{β}{2}+\frac{β^2}{4}=\frac{α^2+β^2}{2}\\ \iff&x^2+y^2-αx-βy+\frac{α^2}{4}+\frac{β^2}{4}=\frac{α^2}{4}+\frac{β^2}{4}\\ \iff&x^2+y^2-αx-βy=0 \quad(1)\end{align}
Είναι όμως \(α+β=10\), οπότε \(β=10-α\) και η εξίσωση \((1)\) γράφεται
$$x^2+y^2-αx-(10-α)y=0.$$
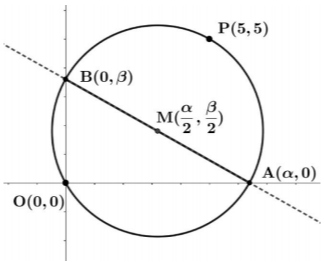
β) Για \(α=1\) έχουμε τον κύκλο:
$$C_1: x^2+y^2-x-9y=0\quad(2)$$
Για \(α=9\) έχουμε τον κύκλο
$$C_2: x^2+y^2-9x-y=0\quad(3)$$
Θα βρούμε τα κοινά σημεία των δύο παραπάνω κύκλων, αν υπάρχουν. Αφαιρώντας κατά μέλη τις εξισώσεις των παραπάνω κύκλων έχουμε
$$8x-8y=0\iff x=y.$$
Tότε από την εξίσωση \((3)\) έχουμε
\begin{align}&x^2+x^2-9x-x=0\\ \iff&2x^2-10x=0\\ \iff&x=0\text{ ή }x=5.\end{align}
Για \(x=0\) έχουμε \(y=0\) και για \(x=5\) έχουμε \(y=5\), άρα οι δύο κύκλοι τέμνονται στα σημεία \(Ο(0,0)\) και \(Ρ(5,5)\). Όλοι οι κύκλοι διέρχονται από το σημείο \(Ρ(5,5)\) αφού οι συντεταγμένες του επαληθεύουν την εξίσωση των κύκλων \(x^2+y^2-αx-(10-α)y=0\).
Πράγματι, αντικαθιστώντας τις τιμές \(x=5\) και \(y=5\) έχουμε
$$5^2+5^2-α\cdot 5-(10-α)\cdot 5=0\iff 0=0.$$
Ομοίως, όλοι οι κύκλοι διέρχονται από την αρχή των αξόνων.
γ) Έστω τυχαίο σημείο \(Μ(x, y)\) είναι σημείο του ζητούμενου γεωμετρικού τόπου, αν και μόνο αν
\begin{align}&\begin{cases}x=\frac{α}{2}\\y=\frac{β}{2}\\α+β=10,\ α > 0,\ β > 0\end{cases}\\ \iff&\begin{cases}α=2x\\β=2y\\α+β=10,\ α > 0,\ β > 0\end{cases}\\ \iff&2x+2y=10\\ \iff&x+y=5.\end{align}
Η παραπάνω ευθεία τέμνει τους άξονες στα σημεία \((5,0)\) και \((0,5)\). Επειδή \(α, β > 0\) έχουμε
$$α > 0\iff 2x > 0\iff x > 0$$
και
$$β > 0\iff y > 0.$$
Συνεπώς ο ζητούμενος γεωμετρικός τόπος είναι το ευθύγραμμο τμήμα \(ΑΒ\), που ορίζεται από την ευθεία \(x+y=5\) με \(x > 0\) και \(y > 0\), εκτός από τα άκρα του \(Α(5,0)\) και \(Β(0,5)\).
Θέμα: 21276
ΘΕΜΑ 4
Σε μια σύγχρονη πόλη κατασκευάζεται σιδηροδρομικό δίκτυο που περιλαμβάνει:
- τη γραμμή \(γ_1\), κάθε σημείο της οποίας στο ορθοκανονικό σύστημα συντεταγμένων είναι της μορφής \(Α(λ-1,\ 2λ+1)\), \(λ\in\mathbb{R}\).
- τη γραμμή \(γ_2\), που περνάει από το σταθμό \(Σ(-4, 2)\) και είναι παράλληλη στο διάνυσμα \(\vec{u}=(-1, 3)\).
α) Να βρείτε τις εξισώσεις των ευθειών πάνω στις οποίες βρίσκονται οι γραμμές \(γ_1\) και \(γ_2\).
(Μονάδες 10)
β) Η είσοδος του αθλητικού σταδίου μιας συνοικίας θα βρίσκεται στο σημείο \(Κ(1, 1)\) του ορθοκανονικού συστήματος συντεταγμένων. Οι κατασκευαστές θέλουν να συνδέσουν την είσοδο του σταδίου απ’ ευθείας με κάθετο δρόμο, με μια από τις γραμμές \(γ_1\) και \(γ_2\). Να βρείτε με ποια από τις δύο γραμμές είναι πιο συμφέρουσα η σύνδεση. Δίνεται ότι το κόστος σύνδεσης ανά μονάδα μήκους είναι το ίδιο και για τις δύο γραμμές.
(Μονάδες 9)
γ) Γύρω από το στάδιο θα δημιουργηθεί κυκλικό πάρκο. Να βρείτε την εξίσωση του κύκλου που θα ορίζει το πάρκο, αν το κέντρο του είναι το σημείο \(Κ\) και επιπλέον ο κύκλος αυτός εφάπτεται της γραμμής \(γ_1\).
(Μονάδες 6)
Απάντηση Θέματος: 21276
α) Έχουμε \(Α(λ-1, 2λ+1)\), \(λ\in\mathbb{R}\), οπότε αν \(Α(x, y)\) τότε:
\begin{align}&\begin{cases}x=λ-1\\y=2λ+1\\λ\in\mathbb{R}\end{cases}\\ \iff&\begin{cases}λ=x+1\\y=2(x+1)+1\\λ\in\mathbb{R}\end{cases}\\ \iff&\begin{cases}y=2x+3\\λ=x+1\\λ\in\mathbb{R}\end{cases}\end{align}
Οπότε \(γ_1: 2x-y+3=0\), η ευθεία πάνω στην οποία βρίσκετε η γραμμή \(γ_1\). Επίσης, ο συντελεστής διεύθυνσης του διανύσματος \(\vec{u}=(-1, 3)\) είναι
$$λ=\frac{y}{x}=\frac{3}{-1}=-3=λ_{γ_2},$$
οπότε η ευθεία πάνω στην οποία βρίσκετε η γραμμή \(γ_2\) έχει εξίσωση
\begin{align}&y-y_Σ=λ_{γ_2}(x-x_Σ)\\ \iff&y-2=-3(x+4)\\ \iff&y-2=-3x-12\\ \iff&3x+y+10=0.\end{align}
β) Είναι \(Κ(1, 1)\), οπότε λόγω του ερωτήματος (α) είναι
\begin{align}d(Κ,γ_1)&=\frac{|2\cdot 1-1\cdot1+3|}{\sqrt{2^2+(-1)^2}}\\ &=\frac{|4|}{\sqrt{5}}\\ &=\frac{4}{\sqrt{5}}\\ &=\frac{4\sqrt{5}}{5}\end{align}
και
\begin{align}d(Κ,γ_2)&=\frac{|3\cdot 1+1\cdot 1+10|}{\sqrt{3^2+1^2}}\\ &=\frac{|14|}{\sqrt{10}}\\ &=\frac{14}{\sqrt{10}}\\ &=\frac{14\sqrt{10}}{10}\\ &=\frac{7\sqrt{10}}{5}.\end{align}
Εφόσον
$$\frac{4\sqrt{5}}{5} < \frac{7\sqrt{10}}{5}\iff d(Κ,γ_1) < d(Κ,γ_2),$$
προφανώς συμφέρει η σύνδεση του σταδίου με τη γραμμή \(γ_1\).
γ) Το κέντρο του ζητούμενου κύκλου που ορίζει το κυκλικό πάρκο γύρω από το στάδιο είναι το σημείο \(Κ(1,1)\). Εφόσον ο κύκλος αυτός εφάπτεται στη γραμμή \(γ_1\), η ακτίνα του λόγω του ερωτήματος (β), είναι \(ρ=d(Κ,γ_1)=\dfrac{4}{\sqrt{5}}\). Επομένως η εξίσωση του κύκλου είναι
\begin{align}&(x-1)^2+(y-1)^2=\left(\frac{4}{\sqrt{5}}\right)^2\\ \iff&(x-1)^2+(y-1)^2=\frac{16}{5}.\end{align}
Θέμα: 21349
ΘΕΜΑ 4
Σε ορθοκανονικό σύστημα αξόνων με αρχή το σημείο \(Ο\) θεωρούμε κύκλο \((C)\) και ευθεία \((ε)\) με εξισώσεις
$$x^2+y^2-9x-3y+10=0\quad (1)$$
και
$$4x+3y-10=0\quad (2)$$
αντίστοιχα.
α) i. Να βρείτε το κέντρο \(Κ\) και την ακτίνα \(R\) του κύκλου \((C)\).
(Μονάδες 5)
ii. Να υπολογίσετε την απόσταση του κέντρου \(Κ\) από την ευθεία \((ε)\) και να αποδείξετε ότι η ευθεία \((ε)\) τέμνει τον κύκλο \((C)\) σε δύο σημεία.
(Μονάδες 4)
iii. Να προσδιορίσετε τα σημεία \(Α\) και \(Β\) στα οποία η ευθεία \((ε)\) τέμνει τον κύκλο \((C)\).
(Μονάδες 5)
β) Αν είναι \(Α(1,2)\) και \(Β(4,-2)\), τότε:
i. Να υπολογίσετε το εσωτερικό γινόμενο \(\overrightarrow{OA}\cdot\overrightarrow{OB}\).
(Μονάδες 5)
ii. Να αποδείξετε ότι ο κύκλος με διάμετρο \(ΑΒ\) διέρχεται από το σημείο \(Ο\).
(Μονάδες 6)
Απάντηση Θέματος: 21349
α) i. Η εξίσωση \((1)\) είναι της μορφής
$$x^2+y^2+Αx+Βy+Γ=0,$$
με \(Α=-9\), \(Β=-3\), \(Γ=10\) και
$$Α^2+Β^2-4Γ=81+9-40=50>0.$$
Επομένως, το κέντρο του κύκλου είναι
$$Κ\left(-\frac{A}{2},-\frac{B}{2}\right)=\left(\frac{9}{2},\frac{3}{2}\right)$$
και η ακτίνα του
$$R=\frac{\sqrt{A^2+B^2-4Γ}}{2}=\frac{\sqrt{50}}{2}=\frac{5\sqrt{2}}{2}.$$
Εναλλακτική λύση (με συμπλήρωση τετραγώνου)
Η εξίσωση \((1)\) γράφεται ισοδύναμα
\begin{align}&x^2+y^2-9x-3y+10=0\\ \iff&x^2-2\cdot\frac{9}{2}x+\left(\frac{9}{2}\right)^2+y^2-2\cdot\frac{3}{2}y+\left(\frac{3}{2}\right)^2=\left(\frac{9}{2}\right)^2+\left(\frac{3}{2}\right)^2-10\\ \iff&\left(x-\frac{9}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=\frac{81}{4}+\frac{9}{4}-\frac{40}{4}\\ \iff&\left(x-\frac{9}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=\frac{50}{4}\\ \iff&\left(x-\frac{9}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=\left(\frac{5\sqrt{2}}{2}\right)^2.\end{align}
ii. Η απόσταση του κέντρου \(Κ\) από την ευθεία \((ε)\) είναι
\begin{align}d(K,ε)&=\frac{|4\cdot\frac{9}{2}+3\cdot\frac{3}{2}-10|}{\sqrt{4^2+3^2}}\\ &=\frac{|\frac{25}{2}|}{5}\\ &=\frac{5}{2} < \frac{5\sqrt{2}}{2}=R.\end{align}
Άρα, η ευθεία \((ε)\) τέμνει τον κύκλο \((C)\) σε δύο σημεία \(Α\) και \(Β\).
iii. Λύνουμε το σύστημα των εξισώσεων \((1)\) και \((2)\). Η εξίσωση \((2)\) γίνεται
$$3y=10-4x\iff y=\frac{10-4x}{3}.$$
Αντικαθιστούμε στην εξίσωση \((1)\), οπότε έχουμε διαδοχικά:
\begin{align}&x^2+\left(\frac{10-4x}{3}\right)^2-9x-3\left(\frac{10-4x}{3}\right)+10=0\\ \iff&x^2+\frac{(10-4x)^2}{9}-9x-(10-4x)+10=0\\ \iff&x^2+\frac{(10-4x)^2}{9}-9x+4x=0\\ \iff&x^2+\frac{(10-4x)^2}{9}-5x=0\\ \iff&9x^2+(100-80x+16x^2)-45x=0\\ \iff&25x^2-125x+100=0\\ \iff&x^2-5x+4=0\quad(3)\end{align}
Οι λύσεις της εξίσωσης \((3)\) είναι \(x=1\), \(x=4\).
Για \(x=1\) είναι \(y=2\), ενώ για \(x=4\) είναι \(y=-2\).
Άρα, τα σημεία τομής της ευθείας \((ε)\) και του κύκλου \((C)\) είναι \(Α(1,2)\) και \(Β(4,-2)\).
β) i. Είναι
$$\overrightarrow{OA}=(x_A-x_O,y_A-y_O)=(1,2)$$
και
$$\overrightarrow{OB}=(x_B-x_O,y_B-y_O)=(4,-2).$$
Οπότε
$$\overrightarrow{OA}\cdot\overrightarrow{OB}=1\cdot 4+2\cdot(-2)=0.$$
ii.
Αφού είναι \(\overrightarrow{OA}\cdot\overrightarrow{OB}=0\), η γωνία \(A\hat{O}B\) θα είναι ορθή. Επομένως, ο κύκλος με διάμετρο \(ΑΒ\) είναι ο περιγεγραμμένος κύκλος του ορθογωνίου τριγώνου \(ΟΑΒ\). Συνεπώς, διέρχεται από το σημείο \(Ο\).
Θέμα: 21962
ΘΕΜΑ 2
Δίνονται τα σημεία \(Α(0,3)\), \(Β(3,4)\) και \(Γ(1,0)\).
α) Να αποδείξετε ότι η γωνία \(B\hat{A}Γ\) είναι ορθή.
(Μονάδες 13)
β) Να βρείτε το μέσο \(Κ\) της υποτείνουσας \(ΒΓ\) του ορθογωνίου τριγώνου \(ΑΒΓ\).
(Μονάδες 5)
γ) Να βρείτε την εξίσωση του κύκλου που διέρχεται από τα σημεία \(Α\), \(Β\) και \(Γ\).
(Μονάδες 7)
Απάντηση Θέματος: 21962
α) Έχουμε ότι
\begin{align}\overrightarrow{AB}&=(x_B-x_A,y_B-y_A)\\ &=(3-0,4-3)\\ &=(3,1)\end{align}
και
\begin{align}\overrightarrow{AΓ}&=(x_Γ-x_A,y_Γ-y_A)\\ &=(1-0,0-3)\\ &=(1,-3).\end{align}
Οπότε
$$\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}=3\cdot 1+1\cdot(-3)=3-3=0,$$
άρα \(\overrightarrow{AB}\perp\overrightarrow{ΑΓ}\) ή \(Β\hat{A}Γ=90^ο\).
β) Το σημείο \(Κ\) που είναι το μέσο του τμήματος \(ΒΓ\) θα έχει συντεταγμένες
$$\left(\frac{x_B+x_Γ}{2},\frac{y_B+y_Γ}{2}\right)=\left(\frac{3+1}{2},\frac{4+0}{2}\right)=(2,2).$$
γ) Από το (α) ερώτημα έχουμε ότι η γωνία \(Β\hat{A}Γ\) είναι ορθή και τα σημεία \(Α\), \(Β\) και \(Γ\) είναι σημεία του ζητούμενου κύκλου, άρα η γωνία \(Β\hat{A}Γ\) είναι εγγεγραμμένη και βαίνει σε ημικύκλιο, συνεπώς η υποτείνουσα \(ΒΓ\) του τριγώνου \(ΑΒΓ\) θα είναι διάμετρος του κύκλου. Είναι
\begin{align}(ΒΓ)&=\sqrt{(x_Γ-x_B)^2+(y_Γ-y_B)^2}\\ &=\sqrt{(1-3)^2+(0-4)^2}\\ &=\sqrt{4+16}\\ &=\sqrt{20}\\ &=2\sqrt{5}.\end{align}
Όμως \(ΒΓ=2R\), άρα \(2R=2\sqrt{5}\) ή \(R=\sqrt{5}\). Ο κύκλος που διέρχεται από τα σημεία \(Α\), \(Β\) και \(Γ\) θα έχει ακτίνα \(R\) και κέντρο το σημείο \(Κ\) του ερωτήματος (β), επομένως η εξίσωσή του θα είναι
$$(x-2)^2+(y-2)^2=5.$$
Θέμα: 22147
ΘΕΜΑ 2
Δίνεται η εξίσωση:
$$x^2+y^2-x-y-\frac{7}{2}=0\quad(1)$$
α) Να αποδείξετε ότι η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο \(K\left(\dfrac{1}{2},\dfrac{1}{2}\right)\) και ακτίνα \(R=2\).
(Μονάδες 9)
β) Να αποδείξετε ότι το σημείο \(Α\left(\dfrac{1}{2},-\dfrac{3}{2}\right)\) είναι σημείο του κύκλου \((Κ,R)\).
(Μονάδες 8)
γ) Να βρείτε την εξίσωση της εφαπτομένης του κύκλου \((Κ,R)\) στο \(Α\).
(Μονάδες 8)
Απάντηση Θέματος: 22147
α) Η εξίσωση \((1)\) είναι της μορφής
$$x^2+y^2+Αx+Βy+Γ=0,$$
με \(Α=-1\), \(Β=-1\), \(Γ=-\dfrac{7}{2}\). Είναι
$$Α^2+Β^2-4Γ=1+1+14=16 > 0,$$
επομένως η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο
$$K\left(-\frac{A}{2},-\frac{B}{2}\right)$$
ή$$K\left(\frac{1}{2},\frac{1}{2}\right)$$
και ακτίνα
\begin{align}R&=\frac{\sqrt{Α^2+Β^2-4Γ}}{2}\\ &=\frac{\sqrt{16}}{2}\\ &=2.\end{align}
β) Οι συντεταγμένες του σημείου \(Α\) επαληθεύουν την εξίσωση του κύκλου, αφού
\begin{align}&\phantom{{}={}}\left(\frac{1}{2}\right)^2+\left(-\frac{3}{2}\right)^2-\frac{1}{2}-\left(-\frac{3}{2}\right)-\frac{7}{2}\\ &=\frac{1}{4}+\frac{9}{4}-\frac{1}{2}+\frac{3}{2}-\frac{7}{2}\\ &=\frac{10}{4}-\frac{5}{2}\\ &=0.\end{align}
Άρα, το σημείο \(Α\) είναι σημείο του κύκλου \((Κ,R)\).
γ) Η εφαπτομένη του κύκλου \((Κ,R)\) στο \(Α\) είναι κάθετη στην ακτίνα \(ΚΑ\). Αφού είναι \(x_K=x_A\), η ακτίνα \(ΚΑ\) είναι κάθετη στον άξονα \(x'x\), οπότε η εφαπτομένη του κύκλου στο \(Α\) θα είναι παράλληλη στον άξονα \(x'x\). Άρα, θα έχει εξίσωση \(y=y_A=-\dfrac{3}{2}\).
Θέμα: 22172
ΘΕΜΑ 2
Θεωρούμε την ευθεία \(ε:3x-4y=0\) και το σημείο \(Α(-2,1)\).
α) Να αποδείξετε ότι η απόσταση του σημείου \(Α\) από την ευθεία είναι \(2\).
(Μονάδες 8)
β) Να βρείτε την εξίσωση ευθείας \((η)\) κάθετης στην \((ε)\) που διέρχεται από το σημείο \(Α\).
(Μονάδες 10)
γ) Να βρείτε την εξίσωση του κύκλου που έχει κέντρο το σημείο \(Α\) και εφάπτεται στην ευθεία \((ε)\).
(Μονάδες 7)
Απάντηση Θέματος: 22172
α) Η απόσταση του σημείου \((x_0,y_0)\) από την ευθεία \(Αx+Βy+Γ=0\) δίνεται από τον τύπο
$$d=\frac{|Ax_0+By_0+Γ|}{\sqrt{A^2+B^2}}.$$
Επομένως έχουμε
\begin{align}d(A,ε)&=\frac{|3\cdot(-2)-4\cdot 1|}{\sqrt{3^2+{(-4)}^2}}\\ &=\frac{|-10|}{\sqrt{25}}\\ &=\frac{10}{5}\\ &=2.\end{align}
β) Η ζητούμενη ευθεία \((η)\) είναι κάθετη στην \((ε)\), οπότε το γινόμενο των συντελεστών διεύθυνσης της \((η)\) και της \((ε)\) θα είναι \(-1\). Ο συντελεστής διεύθυνσης της \((ε)\) είναι
$$λ_2=-\frac{Α}{B}=-\frac{3}{-4}=\frac{3}{4}.$$
Επομένως ο συντελεστής διεύθυνσης \(λ_η\) της ζητούμενης ευθείας \((η)\) θα είναι \(-\dfrac{4}{3}\).
Η ευθεία διέρχεται από το \(Α(-2,1)\), οπότε η εξίσωσή της θα είναι
\begin{align}&y-y_o=λ_η(x-x_o)\\ \iff&y-1=-\frac{4}{3}(x+2)\\ \iff&y=-\frac{4}{3}x-\frac{8}{3}+1\\ \iff&y=-\frac{4}{3}x-\frac{5}{3}.\end{align}
γ) Η εξίσωση κύκλου με κέντρο το σημείο \((x_0,y_0)\) και ακτίνα \(ρ\) είναι η:
$$(x-x_0)^2+(y-y_0)^2=ρ^2\quad(1).$$
Για να εφάπτεται ο κύκλος στην ευθεία \((ε)\), θα πρέπει η απόσταση του κέντρου του \(Α\) από την \((ε)\) να ισούται με την ακτίνα \(ρ\). Στο ερώτημα (α) βρήκαμε ότι η απόσταση του \(Α\) από την \((ε)\) είναι \(2\), επομένως \(ρ=2\) και η \((1)\) γίνεται
\begin{align}&(x-(-2))^2+(y-1)^2=2^2\\ \iff&(x+2)^2+(y-1)^2=4.\end{align}
Θέμα: 22214
ΘΕΜΑ 4
Σε καρτεσιανό επίπεδο \(Οxy\) θεωρούμε τα σημεία \(Μ(x,y)\), \(Α(-1,0)\), \(Β(1,0)\) για τα οποία ισχύει
$$\overrightarrow{AM}^2+\overrightarrow{BM}^2=9|\overrightarrow{AB}|.$$
α) Να αποδείξετε ότι ο γεωμετρικός τόπος των σημείων \(Μ\) είναι ο κύκλος με εξίσωση \(x^2+y^2=8\).
(Μονάδες 10)
β) Έστω \(Γ\) και \(Δ\) δύο σημεία του κύκλου τέτοια ώστε \(ΓΔ^2=32\).
i. Να δείξετε ότι τα σημεία \(Γ\) και \(Δ\) και η αρχή των αξόνων είναι συνευθειακά σημεία.
(Μονάδες 8)
ii. Αν το σημείο \(Μ\) κινείται στον κύκλο, να υπολογίσετε το \(\overrightarrow{MΓ}\cdot\overrightarrow{ΜΔ}\).
(Μονάδες 7)
Απάντηση Θέματος: 22214
α) Είναι
\begin{align}\overrightarrow{AM}&=(x_M-x_A,y_M-y_A)\\ &=(x-(-1),y-0)\\ &=(x+1,y),\\ |\overrightarrow{AM}|&=\sqrt{(x+1)^2+y^2},\\ \overrightarrow{BM}&=(x_M-x_B,y_M-y_B)\\ &=(x-1,y-0)\\ &=(x-1,y),\\ |\overrightarrow{BM}|&=\sqrt{(x-1)^2+y^2},\\ |\overrightarrow{AB}|&=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\\ &=\sqrt{(1-(-1))^2+(0-0)^2}\\ &=\sqrt{2^2+0}\\ &=2\end{align}
και άρα
\begin{align}&\overrightarrow{AM}^2+\overrightarrow{BM}^2=9|\overrightarrow{AB}|\\ \iff&|\overrightarrow{AM}|^2+|\overrightarrow{BM}|^2=9\cdot 2\\ \iff&\left(\sqrt{(x+1)^2+y^2}\right)^2+\left(\sqrt{(x-1)^2+y^2}\right)^2=18\\ \iff&x^2+2x+1+y^2+x^2-2x+1+y^2=18\\ \iff&2x^2+2y^2+2=18\\ \iff&x^2+y^2=8.\end{align}
β) i. Για τα σημεία \(Γ\) και \(Δ\) του κύκλου ισχύει \(Γ∆^2=32\), δηλαδή
$$ΓΔ=\sqrt{32}=\sqrt{16\cdot 2}=4\sqrt{2}.$$
Η εξίσωση του κύκλου είναι \(x^2+y^2=8\), οπότε η ακτίνα του \(ρ\) είναι \(ρ=\sqrt{8}=2\sqrt{2}\) και το κέντρο του το \(Ο(0,0)\). Παρατηρούμε ότι \(ΓΔ=2ρ\), οπότε τα σημεία \(Γ\) και \(Δ\) είναι αντιδιαμετρικά και επομένως η διάμετρος \(ΓΔ\) θα διέρχεται από το κέντρο \(Ο\) του κύκλου.
ii. Αφού η \(ΓΔ\) είναι διάμετρος και το σημείο \(Μ\) είναι σημείο του κύκλου, τότε \(Γ\hat{Μ}∆=90^o\) γιατί είναι εγγεγραμμένη που βαίνει σε ημικύκλιο. Επειδή τα διανύσματα \(\overrightarrow{ΜΓ}\) και \(\overrightarrow{Μ∆}\) είναι κάθετα, το εσωτερικό τους γινόμενο θα ισούται με μηδέν.

Θέμα: 22223
ΘΕΜΑ 4
Σε τρίγωνο \(ΑΒΓ\) είναι \(\overrightarrow{AB}=(λ,λ+1)\), \(\overrightarrow{ΑΓ}=(3λ,λ-1)\) με \(λ\in\mathbb{R}\), και το σημείο \(Μ\) είναι το μέσο της \(ΒΓ\).
α) Να αποδείξετε ότι \(\overrightarrow{ΑΜ}=(2λ,λ)\).
(Μονάδες 8)
β) Δίνεται επιπλέον ότι \(Β\hat{Α}Γ=90^o\).
i. Να υπολογίσετε το \(λ\).
(Μονάδες 8)
ii. Αν \(λ=\frac{1}{2}\) και \(Α\left(2,\dfrac{3}{2}\right)\), να βρείτε την εξίσωση του περιγεγραμμένου κύκλου του τριγώνου \(ΑΒΓ\).
(Μονάδες 9)
Απάντηση Θέματος: 22223
α) Είναι
\begin{align}\overrightarrow{AM}&=\frac{\overrightarrow{AB}+\overrightarrow{AΓ}}{2}\\ &=\frac{(λ,λ+1)+(3λ,λ-1)}{2}\\ &=\frac{(λ+3λ,λ+1+λ-1)}{2}\\ &=\frac{(4λ,2λ)}{2}\\ &=(2λ,λ).\end{align}
β) i. Αφού \(Β\hat{Α}Γ=90^o\), θα είναι
\begin{align}&\overrightarrow{ΑΒ}\perp\overrightarrow{ΑΓ}\\ \iff&\overrightarrow{ΑΒ}\cdot\overrightarrow{ΑΓ}=0\\ \iff&(λ,λ+1)\cdot(3λ,λ-1)=0\\ \iff&3λ^2+(λ-1)(λ+1)=0\\ \iff&3λ^2+λ^2-1=0\\ \iff&4λ^2=1\\ \iff&λ=\pm\frac{1}{2}.\end{align}
ii. Ο ζητούμενος κύκλος διέρχεται από τις κορυφές του τριγώνου \(Α\), \(Β\), \(Γ\). Επειδή όμως η εγγεγραμμένη γωνία \(Β\hat{Α}Γ\) είναι ορθή, η απέναντί πλευρά \(ΒΓ\) θα είναι διάμετρος του κύκλου. Το κέντρο του θα βρίσκεται στο μέσο \(Μ(x,y)\) της διαμέτρου \(ΒΓ\). Από το (α) ερώτημα έχουμε ότι
$$\overrightarrow{AM}=(2λ,λ)=\left(2\cdot\dfrac{1}{2},\dfrac{1}{2}\right)=\left(1,\dfrac{1}{2}\right)$$
και \(Α\left(2,\dfrac{3}{2}\right)\). Όμως
\begin{align}&\overrightarrow{AM}=(x_M-x_A,y_M-y_A)\\ \iff&\left(1,\frac{1}{2}\right)=\left(x_M-2,y_M-\frac{3}{2}\right)\\ \iff&\begin{cases}x_M-2=1\\y_M-\frac{3}{2}=\frac{1}{2}\end{cases}\\ \iff&\begin{cases}x_M=3\\y_M=\frac{1}{2}+\frac{3}{2}=2\end{cases}\end{align}
Επομένως το κέντρο \(Μ\) είναι το \((3,2)\). Η ακτίνα θα είναι η απόσταση
\begin{align}(AM)&=\sqrt{(x_M-x_A)^2+(y_M-y_A)^2}\\ &=\sqrt{(3-2)^2+\left(2-\frac{3}{2}\right)^2}\\ &=\sqrt{1+\left(\frac{1}{2}\right)^2}\\ &=\sqrt{1+\frac{1}{4}}\\ &=\sqrt{\frac{5}{4}}\\ &=\frac{\sqrt{5}}{2}.\end{align}
Η εξίσωση του κύκλου με κέντρο \((x_0,y_0)\) και ακτίνα \(ρ\) δίνεται από την εξίσωση \((x-x_0)^2+(y-y_0)^2=ρ^2\). Για κέντρο το \((3,2)\) και ακτίνα \(\frac{\sqrt{5}}{2}\) έχουμε
\begin{align}&(x-3)^2+(y-2)^2=\left(\frac{\sqrt{5}}{2}\right)^2\\ &(x-3)^2+(y-2)^2=\frac{5}{4}.\end{align}
Θέμα: 22239
ΘΕΜΑ 4
Σε καρτεσιανό σύστημα αξόνων \(Oxy\) η εξίσωση \(3x+4y=25\) περιγράφει τη θέση ενός αγωγού ύδρευσης. Σε αυτό το σύστημα θέλουμε να σχεδιάσουμε ένα κυκλικό σιντριβάνι με κέντρο το \(Ο(0,0)\) και ακτίνα \(2\).
α) i. Ποια είναι η εξίσωση του κύκλου που περιγράφει την θέση του σιντριβανιού;
(Μονάδες 4)
ii. Να εξετάσετε αν ο αγωγός ύδρευσης διέρχεται από το κέντρο του σιντριβανιού, προκειμένου να ενωθεί με αυτό.
(Μονάδες 5)
iii. Αν ο αγωγός ύδρευσης δεν διέρχεται από το κέντρο του σιντριβανιού, ποιο σημείο του αγωγού ύδρευσης πρέπει να ενωθεί με το κέντρο του σιντριβανιού ώστε να έχουμε την μικρότερη δυνατή απόσταση, άρα και οικονομικότερη κατασκευή;
(Μονάδες 8)
β) Ο μηχανικός που θέλει να χαράξει έναν ευθύγραμμο δρόμο, κατέληξε στην εξίσωση \(λx+y+λ-2=0\), με \(λ\neq0\). Μπορείτε να τον βοηθήσετε να βρει για ποια τιμή του \(λ\) ο δρόμος αυτός εφάπτεται του σιντριβανιού;
(Μονάδες 8)
Απάντηση Θέματος: 22239
α) i. Ο κύκλος έχει κέντρο το \(Ο(0,0)\) και ακτίνα \(ρ=2\). Η εξίσωση κύκλου με κέντρο το \(Ο(0,0)\) είναι της μορφής \(x^2+y^2=ρ^2\). Επομένως η εξίσωση γίνεται \(x^2+y^2=4\).
ii. Για να διέρχεται ο αγωγός από το κέντρο \(Ο\) θα πρέπει οι συντεταγμένες του να επαληθεύουν την εξίσωση \(3x+4y=25\), δηλαδή \(3\cdot 0+4\cdot 0=25\), που δεν ισχύει. Επομένως, ο αγωγός δεν διέρχεται από το κέντρο του σιντριβανιού.
iii. Για να έχουμε την ελάχιστη δυνατή απόσταση θα πρέπει να φέρουμε την κάθετη \(ΟΑ\) από το κέντρο \(Ο\) προς την ευθεία του αγωγού. Ο συντελεστής διεύθυνσης της ευθείας του αγωγού είναι \(λ_1=-\dfrac{A}{B}=-\dfrac{3}{4}\). Για να είναι η \(ΑΟ\) κάθετη στον αγωγό πρέπει
\begin{align}&λ_1λ_{ΑΟ}=-1\\ \iff&-\frac{3}{4}λ_{ΑΟ}=-1\\ \iff&λ_{ΑΟ}=\frac{4}{3}.\end{align}
Η εξίσωση της \(ΑΟ\) θα είναι
\begin{align}&y-y_0=λ_{ΑΟ}(x-x_0)\\ \iff&y-0=\frac{4}{3}(x-0)\\ \iff&y=\frac{4}{3}x.\end{align}
Το σημείο \(Α\) είναι το σημείο τομής της \(ΑΟ\) και της ευθείας του αγωγού. Για να βρεθεί λύνουμε το σύστημά τους:
\begin{align}&\begin{cases}3x+4y=25\\y=\frac{4}{3}x\end{cases}\\ \iff&\begin{cases}3x+4\frac{4}{3}x=25\\y=\frac{4}{3}x\end{cases}\\ \iff&\begin{cases}9x+16x=75\\y=\frac{4}{3}x\end{cases}\\ \iff&\begin{cases}25x=75\\y=\frac{4}{3}x\end{cases}\\ \iff&\begin{cases}x=3\\y=4\end{cases}\end{align}
Επομένως το σημείο \(Α\) είναι το \((3,4)\).
β) Για να εφάπτεται ο δρόμος του κυκλικού σιντριβανιού πρέπει η απόσταση του κέντρου \(Ο\) από την ευθεία του δρόμου να ισούται με την ακτίνα του κύκλου, δηλαδή \(d(Ο,ε) = ρ\). Είναι
\begin{align}&d(O,ε)=ρ\\ \iff&\frac{|λ\cdot 0+0+λ+2|}{\sqrt{λ^2+1}}=2\\ \iff&\frac{|λ-2|}{\sqrt{λ^2+1}}=2\\ \iff&|λ-2|=2\sqrt{λ^2+1}\\ \iff&|λ-2|^2=(2\sqrt{λ^2+1})^2\\ \iff&λ^2-4λ+4=4(λ^2+1)\\ \iff&3λ^2+4λ=0\\ \iff&λ(3λ+4)=0.\end{align}
Έχουμε \(λ=0\), που απορρίπτεται λόγω της υπόθεσης \((λ\neq0)\), ή \(λ=-\dfrac{4}{3}\).
Θέμα: 22264
ΘΕΜΑ 4
Δίνεται η εξίσωση
$$x^2+y^2+λx+λy+λ-1=0\quad (1)$$
με \(λ\in\mathbb{R}\).
α) Να αποδείξετε ότι η εξίσωση \((1)\) παριστάνει κύκλο για κάθε \(λ\in\mathbb{R}\).
(Μονάδες 7)
β) Να βρείτε το κέντρο και την ακτίνα του κύκλου που ορίζεται από την εξίσωση \((1)\), ο οποίος εφάπτεται της ευθείας \(ε:x+y+2=0\).
(Μονάδες 9)
γ) Για \(λ=1\), στον κύκλο που προκύπτει από την εξίσωση \((1)\), να βρείτε τις εξισώσεις των εφαπτομένων του που διέρχονται από το σημείο \(Μ\left(-\dfrac{3}{2},-\dfrac{1}{2}\right)\).
(Μονάδες 9)
Απάντηση Θέματος: 22264
α) Έχουμε την εξίσωση
$$x^2+y^2+λx+λy+λ-1=0\quad (1)$$
με \(λ\in\mathbb{R}\), για την οποία \(Α=λ\), \(Β=λ\) και \(Γ=λ-1\), οπότε
\begin{align}Α^2+Β^2-4Γ&=λ^2+λ^2-4(λ-1)\\ &=2λ^2-4λ+4\\ &=2(λ^2-2λ+2)>0\end{align}
για κάθε \(λ\in\mathbb{R}\), εφόσον η διακρίνουσα του τριωνύμου είναι \(Δ=-4< 0\). Άρα η εξίσωση \((1)\) παριστάνει κύκλο για κάθε \(λ\in\mathbb{R}\).
β) Το κέντρο και η ακτίνα των κύκλων που ορίζονται από την \((1)\), συναρτήσει του \(λ\in\mathbb{R}\), είναι το
$$Κ\left(-\dfrac{Α}{2},-\dfrac{Β}{2}\right)=\left(-\dfrac{λ}{2},-\dfrac{λ}{2}\right)$$
και η
\begin{align}ρ&=\frac{1}{2}\sqrt{A^2+B^2-4Γ}\\ &=\frac{1}{2}\sqrt{2(λ^2-2λ+2)}\\ &=\frac{1}{2}\sqrt{2}\sqrt{λ^2-2λ+2},\end{align}
αντίστοιχα. Για να εφάπτεται ο κύκλος που ορίζεται από την \((1)\) της ευθείας \(ε:x+y+2=0\), θα πρέπει
\begin{align}&d(K,ε)=ρ\\ \iff&\frac{|-\frac{λ}{2}-\frac{λ}{2}+2|}{\sqrt{1^2+1^2}}=\frac{1}{2}\sqrt{2}\sqrt{λ^2-2λ+2}\\ \iff&\frac{|-λ+2|}{\sqrt{2}}=\frac{1}{2}\sqrt{2}\sqrt{λ^2-2λ+2}\\ \iff&|2-λ|=\sqrt{λ^2-2λ+2}\\ \iff&|2-λ|^2=\sqrt{λ^2-2λ+2}^2\\ \iff&(2-λ)^2=λ^2-2λ+2\\ \iff&4-4λ+λ^2=λ^2-2λ+2\\ \iff&2λ=2\\ \iff&λ=1.\end{align}
Για \(λ = 1\), το κέντρο του εφαπτόμενου κύκλου στην \(ε\) είναι το \(Κ\left(-\dfrac{1}{2},-\dfrac{1}{2}\right)\) και ακτίνα η \(ρ=\frac{\sqrt{2}}{2}\).
γ) Για \(λ=1\), από την εξίσωση \((1)\) παίρνουμε τον κύκλο \(C:x^2+y^2+x+y=0\), που λόγω του ερωτήματος (β) έχει κέντρο το \(K\left(-\dfrac{1}{2},-\dfrac{1}{2}\right)\) και ακτίνα \(ρ=\dfrac{\sqrt{2}}{2}\). Από το σημείο \(Μ\left(-\dfrac{3}{2},-\dfrac{1}{2}\right)\) διέρχονται οι ευθείες \(ζ\) με εξίσωση
\begin{align}&y-y_M=κ(x-x_M)\\ \iff&y+\frac{1}{2}=κ(x+\frac{3}{2})\\ \iff&2κx-2y+3κ-1=0\end{align}
με \(κ\in\mathbb{R}\). Η ευθεία \(ζ\) εφάπτεται του κύκλου \(C\) αν και μόνο αν
\begin{align}&d(K, ζ)=ρ\\ \iff&\frac{|2κ(-\frac{1}{2})-2(-\frac{1}{2})+3κ-1|}{\sqrt{(2κ)^2+(-2)^2}}=\frac{\sqrt{2}}{2}\\ \iff&\frac{|2κ|}{2\sqrt{κ^2+1}}=\frac{\sqrt{2}}{2}\\ \iff&\frac{|κ|}{\sqrt{κ^2+1}}=\sqrt{2}{2}\\ \iff&\frac{κ^2}{κ^2+1}=\frac{1}{2}\\ \iff&2κ^2=κ^2+1\\ \iff&κ^2=1\\ \iff&κ=\pm1.\end{align}
Για \(κ=1\) προκύπτει η \((ζ_1)\) με εξίσωση
$$2x-2y+2=0\iff x-y+1=0,$$
ενώ για \(κ=-1\) προκύπτει η \((ζ_2)\) με εξίσωση
$$-2x-2y-4=0\iff x+y+2=0.$$
Οι \((ζ_1)\), \((ζ_2)\) είναι οι ζητούμενες εφαπτόμενες του κύκλου \(C\) από το σημείο \(Μ\). Παρατηρούμε ότι η \((ζ_2)\) είναι η ευθεία \((ε)\) που δόθηκε στο ερώτημα (β), κάτι που ήταν αναμενόμενο εφόσον το σημείο \(Μ\) ανήκει στην \((ε)\) (οι συντεταγμένες του επαληθεύουν την εξίσωσή της).
Θέμα: 22279
ΘΕΜΑ 2
Δίνεται η εξίσωση:
$$(y-1)^2=(3+x)(1-x)\quad(1)$$
Να αποδείξετε ότι:
α) Η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο \(Κ(-1,1)\) και ακτίνα \(R=2\).
(Μονάδες 9)
β) Η αρχή \(Ο(0,0)\) των αξόνων είναι εσωτερικό σημείο του κύκλου \((Κ,R)\).
(Μονάδες 7)
γ) Η ευθεία \(ε:x+y=2\) είναι τέμνουσα του κύκλου \((Κ,R)\).
(Μονάδες 9)
Απάντηση Θέματος: 22279
α) Η εξίσωση \((1)\) γράφεται διαδοχικά
\begin{align}&(y-1)^2=(3+x)(1-x)\\ \iff&(y-1)^2=3-3x+x-x^2\\ \iff&(y-1)^2=3-2x-x^2\\ \iff&(x^2+2x+1)+(y-1)^2=4\\ \iff&(x+1)^2+(y-1)^2=4.\end{align}
Άρα, η εξίσωση \((1)\) παριστάνει κύκλο με κέντρο \(Κ(-1,1)\) και ακτίνα \(R=2\).
β) Υπολογίζουμε την απόσταση \(ΟΚ\) της αρχής \(Ο(0,0)\) των αξόνων από το κέντρο \(Κ(-1,1)\) του κύκλου. Είναι
\begin{align}(OK)&=\sqrt{(x_K-x_O)^2+(y_K-y_O)^2}\\ &=\sqrt{(-1-0)^2+(1-0)^2}\\ &=\sqrt{2} < R=2.\end{align}
Άρα, η αρχή \(Ο\) των αξόνων είναι εσωτερικό σημείο του κύκλου \((Κ,R)\).
γ) Υπολογίζουμε την απόσταση του κέντρου \(Κ\) του κύκλου από την ευθεία \((ε)\) με εξίσωση \(x+y-2=0\). Είναι
\begin{align}d(K,ε)&=\frac{|-1+1-2|}{\sqrt{1^2+1^2}}\\ &=\frac{2}{\sqrt{2}}\\ &=\sqrt{2} < R=2.\end{align}
Άρα, η ευθεία \((ε)\) είναι τέμνουσα του κύκλου \((Κ,R)\).
Θέμα: 22280
ΘΕΜΑ 4
Σε ορθοκανονικό σύστημα αξόνων με αρχή το σημείο \(Ο(0,0)\) θεωρούμε τους κύκλους \((Κ,R)\) και \((Λ,ρ)\) με εξισώσεις
$$x^2+y^2-6x-8y+21=0\quad(1)$$
και
$$x^2+y^2+2x-2y+1=0\quad(2)$$
αντίστοιχα.
α) Να βρείτε τα κέντρα και τις ακτίνες των δύο κύκλων.
(Μονάδες 12)
β) Να αποδείξετε ότι οι δύο κύκλοι βρίσκονται ο ένας εξωτερικά του άλλου.
(Μονάδες 8)
γ) Έστω \(Μ\), \(Ν\) τυχαία σημεία των κύκλων \((Κ,R)\) και \((Λ,ρ)\), αντίστοιχα. Να υπολογίσετε την ελάχιστη και τη μέγιστη απόσταση των σημείων \(Μ\) και \(Ν\).
(Μονάδες 5)
Απάντηση Θέματος: 22280
α) Η εξίσωση \((1)\) είναι της μορφής
$$x^2+y^2+Αx+Βy+Γ=0,$$
με \(Α=-6\), \(Β=-8\), \(Γ=21\) και
$$Α^2+Β^2-4Γ=36+64-84=16 > 0.$$
Επομένως, το κέντρο \(Κ\) του κύκλου είναι
$$Κ\left(-\dfrac{A}{2},-\dfrac{B}{2}\right)=(3,4)$$
και η ακτίνα του ισούται με
$$R=\frac{\sqrt{A^2+B^2-4Γ}}{2}=\frac{\sqrt{16}}{2}=2.$$
Η εξίσωση \((2)\) είναι της μορφής
$$x^2+y^2+Αx+Βy+Γ=0,$$
με \(Α=2\), \(Β=-2\), \(Γ=1\) και
$$Α^2+Β^2-4Γ=4+4-4=4>0.$$
Επομένως, το κέντρο \(Λ\) του κύκλου είναι
$$Λ\left(-\frac{A}{2},-\frac{B}{2}\right)=(-1,1)$$
και η ακτίνα του ισούται με
$$ρ=\frac{\sqrt{Α^2+Β^2-4Γ}}{2}=\frac{\sqrt{4}}{2}=1.$$
β) Η απόσταση των κέντρων των δύο κύκλων είναι
\begin{align}(KΛ)&=\sqrt{(x_Λ-x_K)^2+(y_Λ-y_K)^2}\\ &=\sqrt{16+9}\\ &=5.\end{align}
Επίσης, \(R+ρ=3\). Αφού \((KΛ) > R+ρ\), συμπεραίνουμε ότι οι δύο κύκλοι βρίσκονται ο ένας εξωτερικά του άλλου.
γ) Φέρουμε τη διάκεντρο ευθεία \(ΚΛ\), η οποία τέμνει τον κύκλο \((Κ, R)\) στα σημεία \(Ε\) και \(Ζ\) και τον κύκλο \((Λ, ρ)\) στα σημεία \(Α\) και \(Β\), όπως φαίνεται στο σχήμα. Η ελάχιστη απόσταση του τυχαίου σημείου \(Μ\) του κύκλου \((Κ,R)\) από το τυχαίο σημείο \(Ν\) του κύκλου \((Λ,ρ)\) ισούται με \((ΒΕ)\), οπότε
\begin{align}(ΒΕ)&=(ΚΛ)-(ΕΚ)-(ΛΒ)\\ &=(ΚΛ)-R-ρ\\ &=5-2-1\\ &=2.\end{align}
Η μέγιστη απόσταση του τυχαίου σημείου \(Μ\) του κύκλου \((Κ,R)\) από το τυχαίο σημείο \(Ν\) του κύκλου \((Λ,ρ)\) ισούται με \((ΑΖ)\), οπότε
\begin{align}(ΑΖ)&=(ΚΛ)+(ΑΛ)+(ΚΖ)\\ &=(ΚΛ)+R+ρ\\ &=5+2+1\\ &=8.\end{align}
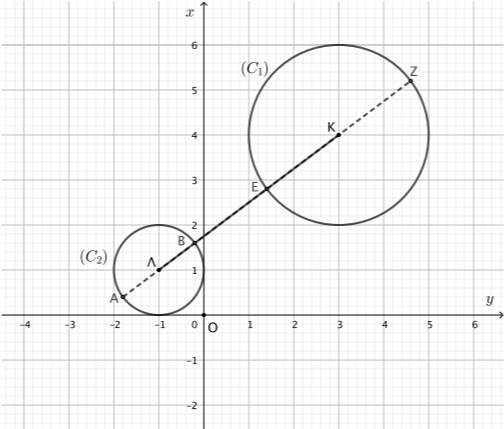
Θέμα: 22508
ΘΕΜΑ 4
Οι κορυφές \(Α\), \(Γ\) ενός τετραγώνου \(ΑΒΓΔ\) είναι τα σημεία \((1,4)\) και \((3,0)\), αντιστοίχως.
α) Να αποδείξετε ότι η εξίσωση της μεσοκαθέτου του ευθυγράμμου τμήματος \(ΑΓ\) γράφεται στη μορφή \(y-2=\dfrac{1}{2}(x-2).\)
(Μονάδες 8)
β) Να αποδείξετε ότι η εξίσωση του κύκλου ο οποίος έχει διάμετρο το ευθύγραμμο τμήμα \(ΑΓ\) γράφεται στη μορφή \((x-2)^2+(y-2)^2=5.\)
(Μονάδες 8)
γ) Να υπολογίσετε τις συντεταγμένες των δύο άλλων κορυφών \(Β\), \(Δ\) του τετραγώνου.
(Μονάδες 9)
Απάντηση Θέματος: 22508
α) Το μέσο \(Κ\) του ευθυγράμμου τμήματος \(ΑΓ\) έχει συντεταγμένες
$$x_K=\frac{x_A+x_Γ}{2}=\frac{1+3}{2}=2$$
και
$$y_K=\frac{y_A+y_Γ}{2}=\frac{4+0}{2}=2.$$
Ο συντελεστής διεύθυνσης της ευθείας \(ΑΓ\) είναι ίσος με
$$λ_1=\frac{4-0}{1-3}=-2,$$
κατά συνέπεια η μεσοκάθετος του τμήματος \(ΑΓ\) έχει συντελεστή διεύθυνσης \(λ_2=\dfrac{1}{2}.\) Άρα η εξίσωση της μεσοκαθέτου του τμήματος \(ΑΓ\) είναι
$$y-2=\frac{1}{2}(x-2).$$
β) Το κέντρο του κύκλου διαμέτρου \(ΑΓ\) είναι το σημείο \(Κ(2,2)\) και η ακτίνα του είναι ίση με
\begin{align}ρ&=(ΑΚ)\\ &=\sqrt{(1-2)^2+(4-2)^2}\\ &=\sqrt{5}.\end{align}
Επομένως η εξίσωση του κύκλου διαμέτρου \(ΑΓ\) είναι
$$(x-2)^2+(y-2)^2=5.$$
γ) Οι ζητούμενες κορυφές \(Β\), \(Δ\) του τετραγώνου \(ΑΒΓΔ\) ισαπέχουν από τα σημεία \(Α\), \(Γ\) και βλέπουν το \(ΑΓ\) υπό ορθή γωνία, άρα είναι τα σημεία τομής της μεσοκαθέτου του τμήματος \(ΑΓ\) και του κύκλου διαμέτρου \(ΑΓ\). Λύνουμε το σύστημα:
$$\begin{cases}y-2=\frac{1}{2}(x-2)\quad&(1)\\(x-2)^2+(y-2)^2=5\quad&(2)\end{cases}$$
Η εξίσωση \((2)\) με τη βοήθεια της \((1)\) γράφεται
\begin{align}&(x-2)^2+\frac{1}{4}(x-2)^2=5\\ \iff&4(x-2)^2+(x-2)^2=20\\ \iff&5(x-2)^2=20\\ \iff&(x-2)^2=4\\ \iff&x-2=\pm2\\ \iff&x=4\text{ ή }x=0.\end{align}
Για \(x=4\) βρίσκουμε \(y=3\) και για \(x=0\) βρίσκουμε \(y=1.\) Επομένως οι ζητούμενες κορυφές είναι τα σημεία \((4,3)\) και \((0,1).\)
Κ32
Θέμα: 18372
ΘΕΜΑ 4
Σε καρτεσιανό επίπεδο \(Οxy\) θεωρούμε τα σημεία \(A(-2,-2)\), \(B(0,-4)\) και την παραβολή \(y^2=4x\).
α) Να βρείτε την παράμετρο, την εστία και την διευθετούσα της παραβολής.
(Μονάδες 9)
β) Να βρείτε το σημείο \(Μ\) της παραβολής στο οποίο η εφαπτομένη της είναι παράλληλη στην \(ΑΒ\).
(Μονάδες 8)
γ) Αν \(Μ(1,-2)\) και \(Κ\) είναι το σημείο τομής της εφαπτομένης ευθείας του προηγούμενου ερωτήματος με τον άξονα \(x'x\), να δείξετε ότι το τετράπλευρο \(ΑΒΜΚ\) είναι παραλληλόγραμμο.
(Μονάδες 8)
Απάντηση Θέματος: 18372
α) Η γενική μορφή της εξίσωσης της παραβολής είναι \(y^2=2px\). Για την \(y^2=4x\) θα έχουμε ότι \(2p=4\), οπότε είναι \(p=2\). Η εστία της \(Ε\) είναι το σημείο \(\left(\dfrac{p}{2},0\right)=(1,0)\).
Η διευθετούσα \((δ)\) έχει εξίσωση \(x=-\dfrac{p}{2}\), δηλαδή \(x=-1\).
β) Η εφαπτομένη της παραβολής στο σημείο της \(Μ(x_1,y_1)\) δίνεται από την εξίσωση \(yy_1=p(x+x_1)\), δηλαδή \(yy_1=2(x+x_1)\). Ο συντελεστής διεύθυνσης της εφαπτομένης, όταν αυτός ορίζεται, είναι \(λ_1=\dfrac{2}{y_1}\), ενώ ο συντελεστής διεύθυνσης της \(ΑΒ\) είναι
$$λ_2=\frac{-4-(-2)}{0-(-2)}=\frac{-2}{2}=-1.$$
Για να είναι η εφαπτομένη παράλληλη στην \(ΑΒ\) πρέπει \(λ_1=λ_2\) ή \(\dfrac{2}{y_1}=-1\), άρα \(y_1=-2\). Επειδή όμως το σημείο \(Μ\) ανήκει στην παραβολή, θα επαληθεύει την εξίσωσή της, δηλαδή \(y_1^2=4x_1\). Αντικαθιστούμε και έχουμε \((-2)^2=4x_1\), άρα \(x_1=1\). Επομένως το σημείο \(Μ\) θα είναι το \((1,-2)\).
γ)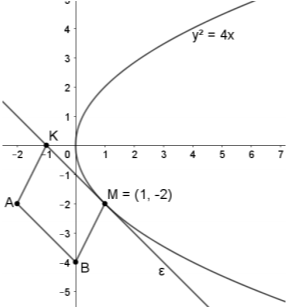
Η εφαπτομένη ευθεία \((ε)\) της παραβολής στο σημείο της \(Μ(1,-2)\) θα είναι
\begin{align}&yy_1=2(x+x_1)\\ \iff&-2y=2(x+1)\\ \iff&-y=x+1\\ \iff&x+y+1=0.\end{align}
Για να βρούμε το σημείο τομής της με τον \(x'x\), βάζουμε όπου $y=0 και έχουμε \(x=-1\). Επομένως το σημείο τομής με τον άξονα \(x'x\) είναι το \(Κ(-1.0)\). Από το ερώτημα (β) γνωρίζουμε ότι \(ΚΜ\parallel ΑΒ\). Επιπλέον,
\begin{align}(ΚΜ)&=\sqrt{(x_M-x_K)^2+(y_M-y_K)^2}\\ &=\sqrt{(1-(-1))^2+(-2-0)^2}\\ &=\sqrt{2^2+2^2}\\ &=\sqrt{8}\end{align}
και
\begin{align}(ΑΒ)&=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\\ &=\sqrt{(0-(-2))^2+(-4-(-2))^2}\\ &=\sqrt{2^2+2^2}\\ &=\sqrt{8}.\end{align}
Τα τμήματα \(ΑΒ\) και \(ΚΜ\) είναι ίσα και παράλληλα, επομένως το τετράπλευρο \(ΑΒΜΚ\) είναι παραλληλόγραμμο, γιατί έχει δύο απέναντι πλευρές του ίσες και παράλληλες.
Θέμα: 18570
ΘΕΜΑ 4
Δίνεται ο κύκλος με εξίσωση
$$x^2+y^2-4x-8y-5=0$$
και η ευθεία
$$ε:3x-4y=μ,\ μ\in\mathbb{R}.$$
α) Να βρείτε το κέντρο του κύκλου και την ακτίνα του.
(Μονάδες 5)
β) Αν η ευθεία \(ε\) τέμνει τον κύκλο σε δύο διαφορετικά σημεία \(Α\), \(Β\):
i. Να αποδείξετε ότι \(-35 < μ < 15\).
(Μονάδες 7)
ii. Να βρείτε για ποια τιμή του \(μ\) η ευθεία \(ε\) διέρχεται από το κέντρο του.
(Μονάδες 4)
iii. Να βρεθεί σημείο \(Γ\) του κύκλου τέτοιο ώστε το τρίγωνο \(ΓΑΒ\) να είναι ισοσκελές με βάση τη χορδή \(ΑΒ\).
(Μονάδες 9)
Απάντηση Θέματος: 18570
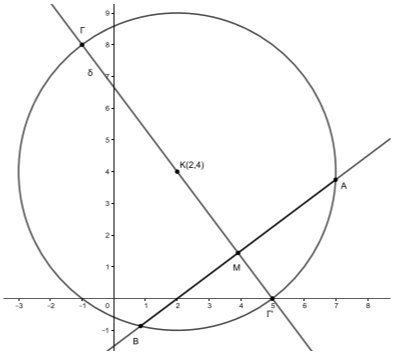
α) Είναι
\begin{align}&x^2+y^2-4x-8y-5=0\\ \iff&x^2-4x+4-4+y^2-8y+16-16-5=0\\ \iff&(x-2)^2+(y-4)^2=25.\end{align}
Άρα το κέντρο του κύκλου είναι το σημείο \(Κ(2,4)\) και η ακτίνα του είναι \(ρ=5\).
β) i. Η ευθεία τέμνει τον κύκλο σε δύο σημεία αν και μόνο αν η απόσταση του κέντρου του από την ευθεία \(ε\) είναι μικρότερη της ακτίνας του. Δηλαδή
\begin{align}&d(K,ε) < ρ\\ \iff&\frac{|3\cdot2-4\cdot4-μ|}{\sqrt{3^2+4^2}} < 5\\ \iff&\frac{|-10-μ|}{5} < 5\\ \iff&|μ+10| < 25\\ \iff&-25 < μ+10 < 25\\ \iff&-35 < μ < 15.\end{align}
ii. Αν η ευθεία \(ε\) διέρχεται από το κέντρο του κύκλου, τότε οι συντεταγμένες του σημείου \(Κ\) θα επαληθεύουν την εξίσωσή της. Δηλαδή
$$3\cdot2-4\cdot4=μ\iff μ=-10.$$
Η τιμή \(μ=-10\) είναι δεκτή, αφού βρίσκεται στο διάστημα \((-35, 15)\) που βρήκαμε στο (β.i) ερώτημα.
iii. Το ζητούμενο σημείο \(Γ\) θα είναι η κορυφή του ισοσκελούς τριγώνου \(ΓΑΒ\) με βάση τη χορδή \(ΑΒ\). Άρα το \(Γ\) θα ανήκει στη μεσοκάθετο ευθεία \(δ\) της χορδής \(ΑΒ\) που είναι ο φορέας του αποστήματος της χορδής αυτής και είναι ευθεία που διέρχεται από το κέντρο \(Κ\) του κύκλου. Ο συντελεστής διεύθυνσης της ευθείας \(ΑΒ\) είναι ο συντελεστής διεύθυνσης της ευθείας \(ε\), δηλαδή \(λ_{ΑΒ}=λ_ε=\dfrac{3}{4}\). Επειδή \(δ\perp ε\), θα είναι
$$λ_δ\cdot λ_ε=-1\iff λ_δ=-\frac{4}{3}.$$
Οπότε η εξίσωση της ευθείας \(δ\) είναι
\begin{align}&y-y_K=-\frac{4}{3}(x-x_K)\\ \iff&y-4=-\frac{4}{3}(x-2)\\ \iff&3y-12=-4x+8\\ \iff&4x+3y=20.\end{align}
Τα σημεία τομής της ευθείας \(δ\) με τον κύκλο είναι τα ζητούμενα σημεία. Λύνουμε το σύστημα των εξισώσεών τους:
\begin{align}&\begin{cases}x^2+y^2-4x-8y-5=0\\y=\frac{1}{3}(20-4x)\end{cases}\\ \iff&\begin{cases}x^2+\frac{1}{9}(20-4x)^2-4x-8\frac{1}{3}(20-4x)-5=0\\y=\frac{1}{3}(20-4x)\end{cases}\\ \iff&\begin{cases}9x^2+400+16x^2-160x-36x-480+96x-45=0\\y=\frac{1}{3}(20-4x)\end{cases}\\ \iff&\begin{cases}x^2-100x-125=0\\y=\frac{1}{3}(20-4x)\end{cases}\\ \iff&\begin{cases}x^2-4x-5=0\\y=\frac{1}{3}(20-4x)\end{cases}\\ \iff&\begin{cases}x=5\\y=0\end{cases}\text{ ή }\begin{cases}x=-1\\y=8\end{cases}\end{align}
Άρα υπάρχουν δύο σημεία του κύκλου τέτοια ώστε το τρίγωνο \(ΓΑΒ\) να είναι ισοσκελές με βάση τη χορδή \(ΑΒ\), τα \(Γ(5,0)\) και \(Γ'(-1,8)\).
Θέμα: 20092
ΘΕΜΑ 4
Δίνεται η παραβολή \(y^2=4x\), το σημείο της \(Μ\left(\dfrac{1}{4},1\right)\) και η ευθεία \(ε\) του επιπέδου με εξίσωση \(ε:\dfrac{x}{3}-\dfrac{y}{4}+1=0\).
α) i. Να δείξετε ότι η ευθεία \(ε\) δεν έχει κοινά σημεία με την παραβολή και να βρείτε την απόστασή του σημείου \(Μ\) από την \(ε\).
(Μονάδες 7)
ii. Αν η ευθεία \(ε\) τέμνει τους άξονες \(x'x\) και \(y'y\) στα σημεία \(Γ\) και \(Δ\) αντίστοιχα, να δείξετε ότι \((ΜΓΔ)=5\) τ.μ.
(Μονάδες 5)
β) i. Να βρείτε την εξίσωση της ευθείας \(ζ\) που εφάπτεται της παραβολής και είναι παράλληλη στην ευθεία \(ε\).
(Μονάδες 8)
ii. Ποια είναι η απόσταση των ευθειών \(ζ\) και \(ε\);
(Μονάδες 5)
Απάντηση Θέματος: 20092
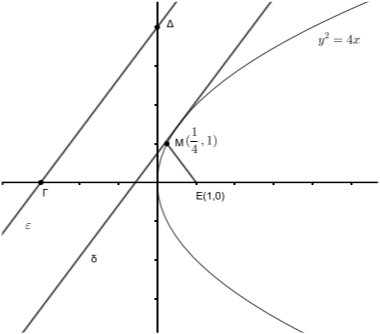
α) i. Αρκεί να δείξουμε ότι το σύστημα των εξισώσεων της παραβολής \(y^2=4x\) και της ευθείας \(\dfrac{x}{3}-\dfrac{y}{4}+1=0\) είναι αδύνατο. Είναι:
\begin{align}&\begin{cases}\frac{x}{3}-\frac{y}{4}+1=0\\y^2=4x\end{cases}\\ \iff&\begin{cases}4x-3y+12=0\\y^2=4x\end{cases}\\ \iff&\begin{cases}y^2-3y+12=0\\y^2=4x\end{cases}\end{align}
Η δευτέρου βαθμού εξίσωση \(y^2-3y+12=0\) δεν έχει πραγματικές ρίζες, αφού \(Δ=9-48< 0\), και άρα το σύστημα είναι πράγματι αδύνατο. Η εξίσωση της ευθείας \(ε\) ισοδύναμα γράφεται \(4x-3y+12=0\), άρα
\begin{align}d(M,ε)&=\frac{|4\cdot\frac{1}{4}-3\cdot 1+12|}{\sqrt{4^2+3^2}}\\ &=\frac{10}{5}\\ &=2.\end{align}
ii. Τα σημεία τομής της ευθείας \(ε\) με τους άξονες τα βρίσκουμε θέτοντας \(y=0\) και \(x=0\) στην εξίσωσή της.
Για \(y=0\) έχουμε \(\dfrac{x}{3}=-1\) ή \(x=-3\), άρα \(Γ(-3,0)\).
Για \(x=0\) έχουμε \(\dfrac{y}{4}=1\) ή \(y=4\), άρα \(Δ(0,4)\).
Για το εμβαδό του τριγώνου \(ΜΓΔ\) θα βρούμε το μήκος του τμήματος \(ΓΔ\) γιατί το ύψος που αντιστοιχεί σε αυτό είναι η απόσταση του σημείου \(Μ\) από την ευθεία \(ε\). Έχουμε
\begin{align}(ΓΔ)&=\sqrt{(-3-0)^2+(0-4)^2}\\ &=\sqrt{9+16}\\ &=\sqrt{25}\\ &=5.\end{align}
Άρα
\begin{align}(MΓΔ)&=\frac{1}{2}(ΓΔ)\cdot d(M,ε)\\ &=\frac{1}{2}\cdot 5\cdot 2\\ &=5\ \text{τ.μ.}\end{align}
β) i. Η εφαπτομένη \(ζ\) της παραβολής σε τυχαίο σημείο της \((x_1,y_1)\) με \(y_1\neq 0\) έχει εξίσωση
$$yy_1=2(x+x_1)\iff y=\frac{2}{y_1}x+\frac{2x_1}{y_1}$$
με συντελεστή διεύθυνσης \(λ_ζ=\dfrac{2}{y_1}\). Η ευθεία \(ε\) έχει συντελεστή διεύθυνσης
$$λ_ε=\frac{4-0}{0-(-3)}=\frac{4}{3}.$$
Για να είναι η ευθεία \(ε\) παράλληλη της εφαπτομένης \(ζ\) πρέπει και αρκεί
\begin{align}&λ_ζ=λ_ε\\ \iff&\frac{4}{3}=\frac{2}{y_1}\\ \iff&y_1=\frac{3}{2}.\end{align}
Το σημείο \((x_1,y_1)\) επαληθεύει την εξίσωση της παραβολής, επομένως
\begin{align}&y_1^2=4x_1\\ \iff&\left(\frac{3}{2}\right)^2=4x_1\\ \iff&x_1=\frac{9}{16}.\end{align}
Για \(x_1=\dfrac{9}{16}\), \(y_1=\dfrac{3}{2}\) η εφαπτομένη \(ζ\) που είναι παράλληλη της ευθείας \(ε\) έχει εξίσωση
\begin{align}&y=\frac{2}{y_1}x+\frac{2x_1}{y_1}\\ \iff&y=\frac{2}{\frac{3}{2}}x+\frac{2\cdot\frac{9}{16}}{\frac{3}{2}}\\ \iff&16x-12y+9=0.\end{align}
ii. Για να βρούμε την απόσταση των ευθειών \(ζ\) και \(ε\), αρκεί να βρούμε ένα σημείο, έστω \(Κ\), της \(ζ\) και να υπολογίσουμε την απόσταση του σημείου αυτού από την ευθεία \(ε\). Θέτοντας \(x=0\) στην εξίσωση της ευθείας \(ζ\) έχουμε \(y=\dfrac{9}{12}=\dfrac{3}{4}\). Άρα το σημείο \(Κ\) της ευθείας \(ζ\) είναι το \(Κ\left(0,\dfrac{3}{4}\right)\). Η εξίσωση της ευθείας \(ε\) είναι \(4x-3y+12=0\), επομένως
\begin{align}d(ζ,ε)&=d(K,ε)\\ &=\frac{|4\cdot 0-3\cdot\frac{3}{4}+12|}{\sqrt{4^2+(-3)^2}}\\ &=\frac{|-\frac{9}{4}+\frac{48}{4}|}{\sqrt{25}}\\ &=\frac{\frac{39}{4}}{5}\\ &=\frac{39}{20}.\end{align}
Θέμα: 20235
ΘΕΜΑ 2
Δίνεται η παραβολή \(C:\ y^2 = 8x\).
α) Να βρείτε την εστία και την διευθετούσα της παραβολής.
(Μονάδες 10)
β) Να αποδείξετε ότι η εφαπτομένη της παραβολής στο σημείο της \(\left(\dfrac{1}{8} ,1\right)\) είναι παράλληλη στην ευθεία \((ε): 8x – 2y + 3 = 0.\)
(Μονάδες 15)
Απάντηση Θέματος: 20235
α) Είναι: \(C:\ y^2 = 2\cdot 4x\), οπότε \(p = 4\), άρα \(Ε\left( \dfrac{p}{2} , 0\right) = (2 , 0)\) είναι η εστία και \((δ):\ x = - \dfrac{p}{2} \Leftrightarrow x = - 2\), είναι η διευθετούσα.
β) Η εφαπτομένη της παραβολής \(C\) στο \(\left(\dfrac{1}{8} ,1\right)\) είναι:
$$\begin{align} (ε_1):\ & yy_1 = p(x + x_1) \\ \Leftrightarrow (ε_1):\ & y\cdot 1 = 4(x + 18) \\ \Leftrightarrow (ε_1):\ & y = 4x + 12 \text{ με } 𝜆_{𝜀_1}=4 \end{align}$$
Επίσης για την ευθεία \((ε):\ 8x – 2y + 3 = 0\) είναι: \(𝜆_𝜀 =-\dfrac{Α}{Β} = -\dfrac{8}{−2} =4.\)
Οπότε \(𝜆_{𝜀_1}= 𝜆_𝜀\) επομένως: \((ε_1)\parallel (ε).\)
Θέμα: 21152
ΘΕΜΑ 1
α) Να χαρακτηρίσετε καθεμιά από τις προτάσεις που ακολουθούν ως Σωστή (Σ) ή Λανθασμένη (Λ), γράφοντας στην κόλλα σας, δίπλα στον αριθμό που αντιστοιχεί σε καθεμιά από αυτές το γράμμα Σ αν η πρόταση είναι Σωστή, ή το γράμμα Λ αν αυτή είναι Λάθος.
i. Κάθε διάνυσμα στον χώρο είναι ίσο με τη διανυσματική ακτίνα του πέρατος μείον τη διανυσματική ακτίνα της αρχής.
ii. Η ευθεία που διέρχεται από το σημείο \(Α(x_0, y_0)\) και είναι παράλληλη στον άξονα \(x΄x\) έχει εξίσωση \(x = x_0.\)
iii. Η ευθεία με εξίσωση \(Ax+By+Γ=0\) είναι παράλληλη στο διάνυσμα \(\vec{η}=(Α,Β).\)
iv. Η παραβολή με εξίσωση \(y^2=4x\) έχει εστία το σημείο \(Ε(1,0).\)
v. Η εφαπτομένη του κύκλου \(x^2+y^2=ρ^2\) στο σημείο του \(Α(x_1,y_1)\) έχει εξίσωση \(xx_1+yy_1=ρ^2.\)
(Μονάδες 10)
β) Να αποδείξετε ότι η εξίσωση της ευθείας που διέρχεται από το σημείο \(Α(x_0, y_0)\) και έχει συντελεστή διεύθυνσης \(λ\) είναι \(y−y_0=λ(x−x_0)\)
(Μονάδες 15)
Απάντηση Θέματος: 21152
Απαντήσεις
α)
- i. Σωστό, Σελίδα 19 σχολικό βιβλίο.
- ii. Λάθος, Η ευθεία που διέρχεται από το σημείο \(Α(x_0, y_0)\) και είναι παράλληλη στον άξονα \(x΄x\) έχει εξίσωση \(y= y_0.\)
- iii. Λάθος, Η ευθεία με εξίσωση \(Ax+By+Γ=0\) είναι κάθετη στο διάνυσμα \(\vec{η}=(Α,Β).\)
- iv. Σωστό, Σελίδα 91 σχολικό βιβλίο.
- v. Σωστό, Σελίδα 83 σχολικό βιβλίο.
β) Σελίδα 60 σχολικό βιβλίο – Εξίσωση ευθείας.
Θέμα: 21306
ΘΕΜΑ 2
Σε καρτεσιανό επίπεδο \(Οxy\) δίνεται η παραβολή με άξονα συμμετρίας τον \(x'x\), κορυφή \(Ο(0,0)\) και εστία \(Ε(2,0)\), όπως στο παρακάτω σχήμα. Το σημείο \(Α\) της παραβολής έχει τετμημένη \(3\) και βρίσκεται στο πρώτο τεταρτημόριο του \(Οxy\).
α) Να αποδείξετε ότι η εξίσωση της παραβολής είναι \(y^2=8x\) και ότι \(A(3,2\sqrt{6})\).
(Μονάδες 10)
β) Να σχεδιάσετε τη διευθετούσα \((δ)\) της παραβολής και να γράψετε την εξίσωσή της.
(Μονάδες 6)
γ) Να βρείτε την εξίσωση της εφαπτομένη \((ε)\) της παραβολής στο σημείο \(Α\).
(Μονάδες 9)
Απάντηση Θέματος: 21306
α) Η παραβολή με άξονα συμμετρίας τον \(x'x\) και κορυφή \(Ο(0,0)\) έχει εξίσωση \(y^2=2px\) και εστία \(E\left(\dfrac{p}{2},0\right)\). Άρα \(\dfrac{p}{2}=2\) ή \(p=4\) και η εξίσωση της παραβολής είναι
$$y^2=2\cdot 4\cdot x\iff y^2=8x.$$
Το σημείο \(A(3,y_A)\) της παραβολής έχει \(y_A > 0\), εφόσον βρίσκεται στο πρώτο τεταρτημόριο του \(Oxy\). Οι συντεταγμένες του επαληθεύουν την εξίσωση της παραβολής. Επομένως
\begin{align}&y_A^2=8\cdot3\\ \iff& y_A^2=24\\ \iff& y_A=\sqrt{24}=2\sqrt{6}.\end{align}
β) Η διευθετούσα \((δ)\) της παραβολής είναι η κατακόρυφη ευθεία \(x=-\dfrac{p}{2}\). Για \(p=4\), δηλαδή, είναι η \(x=-2\), την οποία σχεδιάζουμε στο παρακάτω σχήμα.
γ) Η εξίσωση της εφαπτομένης \((ε)\) της παραβολής στο σημείο της \(Α\) έχει εξίσωση \(yy_A=p(x+x_A)\). Αντικαθιστούμε ως \(x_A\) και \(y_A\) τις συντεταγμένες του σημείου \(Α\) και \(p=4\) και παίρνουμε
\begin{align}&2\sqrt{6}y=4(x+3)\\ \iff&2\sqrt{6}y=4x+12\\ \iff&4x-2\sqrt{6}y+12=0\\ \iff&2x-\sqrt{6}y+6=0.\end{align}
Θέμα: 21307
ΘΕΜΑ 2
Σε καρτεσιανό επίπεδο \(Οxy\) δίνεται η παραβολή με εξίσωση \(x^2=12y\).
α) Να αποδείξετε ότι η εστία της παραβολής είναι το σημείο \(E(0,3)\) και να βρείτε τα σημεία της παραβολής που έχουν τεταγμένη \(3\).
(Μονάδες 12)
β) Να αποδείξετε ότι εφαπτομένες \((ε_1)\) και \((ε_2)\) της παραβολής στα σημεία \(Α(6,3)\) και \(Β(-6,3)\), αντίστοιχα, έχουν εξισώσεις \(y=x-3\) και \(y=-x-3\).
(Μονάδες 8)
γ) Να βρείτε το σημείο τομής των \((ε_1)\) και \((ε_2)\).
(Μονάδες 5)
Απάντηση Θέματος: 21307
α) Για την παραβολή \(x^2=12y\) ή \(x^2=2\cdot 6y\) είναι \(p=6\), άρα η εστία της είναι το \(E\left(0,\dfrac{p}{2}\right)\) ή \(E(0,3)\). Το σημείο \((x_0,3)\) ανήκει στην παραβολή, άρα
\begin{align}&x_0^2=12\cdot 3\\ \iff&x_0^2=36\\ \iff&x_0=\pm6.\end{align}
Επομένως \(A(6,3)\) και \(B(-6,3)\) είναι τα ζητούμενα σημεία.
β) Η εξίσωση της εφαπτομένης της παραβολής στο σημείο της \((x_1,y_1)\) έχει εξίσωση \(xx_1=p(y+y_1)\). Για την \((ε_1)\) με σημείο επαφής το \(A(6,3)\) αντικαθιστούμε ως \(x_1\) και \(y_1\) τις συντεταγμένες του σημείου \(Α\) και \(p=6\), άρα έχουμε
\begin{align}&6x=6(y+3)\\ \iff&6x=6y+18\\ \iff&x=y+3\\ \iff&y=x-3.\end{align}
Αντίστοιχα, για την \((ε_2)\) με σημείο επαφής το \(Β(-6,3)\) αντικαθιστούμε ως \(x_1\) και \(y_1\) τις συντεταγμένες του σημείου \(B\) και \(p=6\). Έτσι έχουμε
\begin{align}&-6x=6(y+3)\\ \iff&-6x=6y+18\\ \iff&-x=y+3\\ \iff&y=-x-3.\end{align}
γ) Βρίσκουμε το σημείο τομής των \((ε_1): y=x-3\) και \((ε_2): y=-x-3\) λύνοντας το σύστημα των εξισώσεών τους:
\begin{align}&\begin{cases}y=x-3\\y=-x-3\end{cases}\\ \iff&\begin{cases}y=x-3\\2y=-6\end{cases}\\ \iff&\begin{cases}-3=x-3\\y=-3\end{cases}\\ \iff&\begin{cases}x=0\\y=-3\end{cases}\end{align}
Άρα το σημείο τομής των \((ε_1)\) και \((ε_2)\) είναι το σημείο \((0,-3)\).
Θέμα: 21883
ΘΕΜΑ 4
Δίνεται η παραβολή \(C:x^2=4y\) και η ευθεία \(ε:y=x-2.\)
α) Να βρείτε την εστία \(Ε\) και τη διευθετούσα \((δ)\) της παραβολής.
(Μονάδες 5)
β) Να αποδείξετε ότι η ευθεία και η παραβολή δεν έχουν κοινά σημεία. Στη συνέχεια, σε ένα ορθοκανονικό σύστημα αξόνων \(Oxy\) να σχεδιαστούν οι γραφικές παραστάσεις της παραβολής \(C\) και της ευθείας \(ε\).
(Μονάδες 8)
γ) Αν \(Μ(x,y)\) είναι σημείο της παραβολής, τότε:
i. Nα αποδείξετε ότι η απόσταση του \(M\) από την ευθεία \((ε)\) είναι \(d(M,ε)=\dfrac{\frac{1}{4}x^2-x+2}{\sqrt{2}}.\)
(Μονάδες 6)
ii. Να βρείτε την ελάχιστη απόσταση του σημείου \(Μ\) από την ευθεία \((ε)\) καθώς και τις συντεταγμένες του σημείου \(Μ\) της παραβολής που απέχει την ελάχιστη απόσταση από την ευθεία.
(Μονάδες 6)
Απάντηση Θέματος: 21883
α) Η παράμετρος της παραβολής είναι \(p=2\), άρα η εστία είναι το \(E\left(0,\dfrac{p}{2}\right)=(0,1)\) και η εξίσωση της διευθετούσας \(δ:y=-1.\)
β) Τα κοινά σημεία της παραβολής και της ευθείας είναι οι λύσεις του συστήματος των εξισώσεών τους
\begin{align}&\begin{cases}x^2=4y\\y=x-2\end{cases}\\ \iff&\begin{cases}x^2=4(x-2)\\y=x-2\end{cases}\\ \iff&\begin{cases}x^2-4x+8=0\\y=x-2\end{cases}\end{align}
το οποίο είναι αδύνατο εφόσον \(Δ < 0\). Άρα η ευθεία και η παραβολή δεν έχουν κοινά σημεία.
γ) i. Έστω σημείο \(Μ(x,y)\) σημείο της παραβολής, οπότε \(Μ\left(x,\dfrac{1}{4}x^2\right).\) Η απόστασή του από την ευθεία \(ε: x-y-2=0\) είναι
\begin{align}d(M,ε)&=\frac{|x-\frac{1}{4}x^2-2|}{\sqrt{2}}\\ &=\frac{|\frac{1}{4}x^2-x+2|}{\sqrt{2}}\\ &=\frac{\frac{1}{4}x^2-x+2}{\sqrt{2}},\end{align}
διότι η διακρίνουσα του τριωνύμου \(\dfrac{1}{4}x^2-x+2\) είναι
$$Δ=1-4\cdot\frac{1}{4}\cdot2=-1 < 0$$
και άρα \(\dfrac{1}{4}x^2-x+2 > 0\) για κάθε πραγματικό αριθμό \(x.\)
ii. Είναι
\begin{align}d(M,ε)&=\frac{\frac{1}{4}x^2-x+2}{\sqrt{2}}\\ &=\frac{\left(\frac{1}{2}x-1\right)^2+1}{\sqrt{2}}\\ &\geq\frac{1}{\sqrt{2}}\\ &=\frac{\sqrt{2}}{2}.\end{align}
Η απόσταση του \(Μ\) από την ευθεία γίνεται ελάχιστη όταν
\begin{align}&\left(\frac{1}{2}x-1\right)^2=0\\ \iff&\frac{1}{2}x-1=0\\ \iff&x=2.\end{align}
Επομένως το ζητούμενο σημείο της παραβολής που απέχει ελάχιστη απόσταση από την ευθεία \((ε)\) είναι το \(Μ(2,1).\)
Θέμα: 22190
ΘΕΜΑ 2
Δίνεται η παραβολή \((C)\) με εξίσωση:
$$y^2=x\quad(1)$$
α) Να βρείτε τις συντεταγμένες της εστίας \(Ε\) και την εξίσωση της διευθετούσας \((δ)\).
(Μονάδες 12)
β) Να αποδείξετε ότι το σημείο \(Α(1,-1)\) είναι σημείο της παραβολής.
(Μονάδες 5)
γ) Να βρείτε την εξίσωση της εφαπτομένης παραβολής στο σημείο της \(Α(1,-1)\).
(Μονάδες 8)
Απάντηση Θέματος: 22190
α) Αρχικά υπολογίζουμε την παράμετρο \(p\) της παραβολής. Είναι
$$2p=1\iff p=\frac{1}{2}.$$
Η εστία \(Ε\) της παραβολής έχει συντεταγμένες \(E\left(\dfrac{p}{2},0\right)=\left(\dfrac{1}{4},0\right)\). Η διευθετούσα \((δ)\) της παραβολής έχει εξίσωση \(x=-\dfrac{p}{2}=-\dfrac{1}{4}\).
β) Εξετάζουμε αν οι συντεταγμένες του σημείου \(Α\) επαληθεύουν την εξίσωση της παραβολής. Για \(x=1\) και \(y=-1\) είναι \((-1)^2=1\). Η τελευταία ισότητα είναι αληθής, οπότε το σημείο \(Α\) είναι σημείο της παραβολής.
γ) Η εξίσωση της εφαπτομένης της παραβολής \(y^2=2px\) στο σημείο της \(Α(x_1,y_1)\) είναι \(yy_1=p(x+x_1)\). Αφού δίνεται \(Α(1,-1)\), η ζητούμενη εξίσωση θα είναι
$$-1\cdot y=\frac{1}{2}(x+1)\iff x+2y+1=0.$$
Θέμα: 22267
ΘΕΜΑ 2
Δίνεται η εξίσωση:
$$y^2=4x\quad (1)$$
α) Να γράψετε στο τετράδιό σας συμπληρωμένη την παρακάτω πρόταση: «Τα σημεία του επιπέδου που επαληθεύουν την εξίσωση \((1)\) βρίσκονται σε μια καμπύλη που ονομάζεται ………………….. Η εστία της, \(Ε\), έχει συντεταγμένες \(Ε(\dots, \dots)\) και η διευθετούσα έχει εξίσωση ………….».
(Μονάδες 9)
β) Να βρείτε την εξίσωση της ευθείας \((ε)\) που εφάπτεται στην παραπάνω καμπύλη στο σημείο \(Α(1,-2)\).
(Μονάδες 8)
γ) Να αποδείξετε ότι το σημείο τομής της ευθείας \((ε)\) με τον άξονα \(x'x\) είναι σημείο της διευθετούσας της παραβολής.
(Μονάδες 8)
Απάντηση Θέματος: 22267
α) Η εξίσωση \((1)\) είναι της μορφής \(y^2=2px\), όπου \(2p=4\), άρα \(p=2\). Η εξίσωση αυτής της μορφής παριστάνει τα σημεία του επιπέδου που βρίσκονται σε παραβολή με εστία στον άξονα \(x'x\). Η εστία της είναι το σημείο \(Ε\left(\dfrac{p}{2}, 0\right)\) και η διευθετούσα της έχει εξίσωση \(x=-\dfrac{p}{2}\). «Τα σημεία του επιπέδου που επαληθεύουν την εξίσωση \((1)\) βρίσκονται σε μια καμπύλη που ονομάζεται παραβολή. Η εστία της, \(Ε\), έχει συντεταγμένες \(Ε(1, 0)\) και η διευθετούσα έχει εξίσωση \(x=-1\) ».
β) Η εφαπτόμενη ευθεία σε σημείο με συντεταγμένες \((x_1,y_1)\) της παραβολής έχει εξίσωση \(yy_1=p(x+x_1)\), και επειδή \(p=2\), η εφαπτόμενη \((ε)\) θα είναι \(ε:yy_1=2(x+x_1)\). Δίνεται το σημείο επαφής \(Α(1,-2)\), οπότε η εξίσωση της ευθείας \((ε)\) για \(x_1=1\) και \(y_1=-2\) θα είναι
$$-2y=2(x+1)\iff y=-x-1.$$
γ) Για να βρούμε το σημείο τομής της ευθείας \((ε)\) με τον άξονα \(x'x\) θέτουμε \(y=0\) στην εξίσωση της ευθείας \((ε)\). Οπότε, έχουμε
$$-x-1=0\iff x=-1,$$
δηλαδή το σημείο τομής της ευθείας \((ε)\) με τον άξονα \(x'x\) είναι το σημείο \((-1,0)\), το οποίο είναι σημείο της διευθετούσας, αφού η εξίσωσή της είναι η \(x=-1\).
Θέμα: 22465
ΘΕΜΑ 4
Έστω παραβολή \((C)\) με κορυφή την αρχή των αξόνων \(Ο\) και άξονα συμμετρίας τον \(x'x\). Η απόσταση της εστίας \(Ε\) από την διευθετούσα \((δ)\) της παραβολής \((C)\) είναι \(4\) και η γραφική της παράσταση φαίνεται στο παρακάτω ορθοκανονικό σύστημα αξόνων.
α) Να αποδείξετε ότι η εστία της είναι η \(Ε(2,0)\), η διευθετούσα της είναι η \(δ: x=-2\), και η εξίσωσή της παραβολής είναι \(y^2=8x.\)
(Μονάδες 9)
β) Να αποδείξετε ότι η εξίσωση της εφαπτομένης της παραβολής στο σημείο της \(Α(2,4)\) είναι η \(ε:y=x+2.\)
(Μονάδες 9)
γ) Να βρείτε την εξίσωση του κύκλου που διέρχεται από την εστία της παραβολής και εφάπτεται στην ευθεία \((ε)\) στο σημείο της \(Α(2,4)\).
(Μονάδες 7)
Απάντηση Θέματος: 22465
α) Αν \(p\) η παράμετρος της παραβολής, τότε η τιμή \(|p|\) παριστάνει την απόσταση της εστίας από την διευθετούσα, και εφόσον η εστία της παραβολής μας είναι στο θετικό ημιάξονα \(x'x\), είναι \(p > 0\), άρα \(p=4\). Οι συντεταγμένες της εστίας της είναι \(Ε\left(\dfrac{p}{2},0\right)\), άρα \(Ε(2,0)\). Η διευθετούσα της έχει εξίσωση \(x=-\dfrac{p}{2}=-2\) και η εξίσωση της παραβολής είναι \(y^2=2px=8x.\)
β) Η εξίσωση της εφαπτομένης της παραβολής \(y^2=2px\) στο σημείο της \(Α(x_1,y_1)\) είναι η \(yy_1=p(x+x_1)\), άρα η εφαπτομένη \((ε)\) της παραβολής μας στο σημείο της \(Α(2,4)\) έχει εξίσωση
$$4y=4(x+2)\iff y=x+2.$$
γ)
Αν \(Κ\) το κέντρο του ζητούμενου κύκλου, η ευθεία \(ΚΑ\) είναι κάθετη στην ευθεία \((ε)\), επομένως το γινόμενο των συντελεστών διεύθυνσης των είναι \(-1\), και αφού ο συντελεστής διεύθυνσης της \((ε)\) είναι \(1\), έχουμε \(λ_{ΑΚ}=-1\). Η ευθεία \(ΑΚ\) διέρχεται από το σημείο \(Α(2,4)\) και έχει συντελεστή διεύθυνσης \(-1\), επομένως η εξίσωσή της είναι
$$y-4=-(x-2)\iff y=-x+6.$$
Το κέντρο \(Κ\) του κύκλου ισαπέχει από το σημείο \(Α(2,4)\) και την εστία \(Ε(2,0)\), άρα βρίσκεται πάνω στη μεσοκάθετη του τμήματος \(ΑΕ\). Εφόσον τα σημεία \(Α\) και \(Ε\) έχουν την ίδια τετμημένη, η ευθεία \(ΑΕ\) είναι κάθετη στον άξονα \(x'x.\)
Το μέσον του τμήματος \(ΑΕ\) είναι το σημείο \((2,2)\). Έτσι, η μεσοκάθετη του τμήματος \(ΑΕ\) είναι η ευθεία \(y=2\), και επομένως η τεταγμένη του κέντρου \(Κ\) είναι \(y=2.\) Θέτοντας \(y=2\) στην εξίσωση της ευθείας \(ΑΚ\) έχουμε \(2=-x+6\), άρα \(x=4.\)
Άρα, το κέντρο του ζητούμενου κύκλου είναι το \(Κ(4,2).\) Η ακτίνα του ζητούμενου κύκλου είναι
$$ρ=(ΚΕ)=\sqrt{(4-2)^2+2^2}=\sqrt{8}.$$
Τελικά η εξίσωση του ζητούμενου κύκλου είναι
$$(x-4)^2+(y-2)^2=8.$$
ΚΕΕ ΕΛΛΕΙΨΗ
Θέμα: 20883
ΘΕΜΑ 2
Δίνεται η εξίσωση της έλλειψης \(C: 16x^2+25y^2=400\).
α) Να βρείτε τα μήκη \(ΒΒ'\), \(ΑΑ'\) του μικρού και τον μεγάλου άξονα της έλλειψης, καθώς και τις εστίες της \(Ε\) και \(Ε'\).
(Μονάδες 12)
β) Αν \(Ε'(-3,0)\) και \(Ε(3,0)\), να γράψετε την εξίσωση της παραβολής που έχει εστία το σημείο \(Ε'\) και διευθετούσα την ευθεία που διέρχεται από το \(Ε\) και είναι παράλληλη στον άξονα \(y'y\).
(Μονάδες 13)
Απάντηση Θέματος: 20883
α) Είναι \(C: 16x^2+25y^2=400\) ή \(C:\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\), οπότε
$$α^2=25\iff α=5$$
και άρα
$$(Α'Α)=2α=2\cdot 5=10$$
είναι το μήκος του μεγάλου άξονα. Επίσης
$$β^2=16\iff β=4,$$
άρα
$$(Β'Β)=2β=2\cdot 4=8$$
είναι το μήκος του μικρού άξονα. Ακόμη
$$γ^2=α^2-β^2=25-16=9,$$
οπότε \(γ=3\). Άρα \(Ε'(-γ,0)\) και \(Ε(γ,0)\) ή \(Ε'(-3,0)\) και \(Ε(3,0)\) είναι οι εστίες της έλλειψης.
β) Έχουμε \(Ε'(-3,0)\) και \(Ε(3,0)\). Θέλουμε η \(Ε'\) να είναι εστία της ζητούμενης παραβολής, άρα
$$\frac{p}{2}=-3\iff p=-6,$$
και επομένως η ζητούμενη εξίσωση είναι
\begin{align}&y^2=2px\\ \iff&y^2=2\cdot(-6)x\\ \iff&y^2=-12x.\end{align}
Θέμα: 21308
ΘΕΜΑ 2
Σε καρτεσιανό επίπεδο \(Οxy\) δίνεται η έλλειψη \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\). Να βρείτε:
α) Τις συντεταγμένες των εστιών \(Ε\) και \(E'\) της έλλειψης και την απόστασή τους.
(Μονάδες 9)
β) Το μήκος του μικρού άξονα και το μήκος του μεγάλου άξονα της έλλειψης.
(Μονάδες 8)
γ) Την εξίσωση της εφαπτομένης \((ε)\) της έλλειψης στο σημείο της \(B(0,4)\).
(Μονάδες 8)
Απάντηση Θέματος: 21308
α) Η εξίσωση της έλλειψης είναι της μορφής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1\) με \(α=5\) και \(β=4\). Επομένως έχει εστίες της μορφής \(Ε(γ,0)\) και \(E'(-γ,0)\), με \(γ>0\), όπου
\begin{align}&β=\sqrt{α^2-γ^2}\\ \iff&β^2=α^2-γ^2\\ \iff&γ^2=α^2-β^2.\end{align}
Αντικαθιστώντας \(α=5\) και \(β=4\) έχουμε
\begin{align}&γ^2=5^2-4^2\\ \iff&γ^2=25-16\\ \iff&γ^2=9\\ \iff&γ=3,\end{align}
εφόσον \(γ >0\). Άρα οι εστίες της έλλειψης είναι οι \(Ε(3,0)\) και \(E'(-3,0)\). Η απόσταση των εστιών είναι \(2γ=2\cdot 3=6\).
β) Ο μικρός άξονας της έλλειψης έχει μήκος \(2β=2\cdot 4=8\). Ο μεγάλος άξονας της έλλειψης έχει μήκος \(2α=2\cdot 5=10\).
γ) Από τη θεωρία, η εφαπτομένη \((ε)\) της έλλειψης της μορφής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1\) στο σημείο της \((x_1,y_1)\) έχει εξίσωση
$$\frac{x\cdot x_1}{α^2}+\frac{y\cdot y_2}{β^2}=1.$$
Αντικαθιστώντας όπου \(x_1\) και \(y_1\) τις συντεταγμένες του σημείου \(Β\) της έλλειψης και όπου \(α=5\) και \(β=4\), έχουμε
$$\frac{0x}{25}+\frac{4y}{16}=1\iff y=4$$
που είναι η εξίσωση της (\(ε\)).
Θέμα: 22168
ΘΕΜΑ 2
Δίνονται η παραβολή \(y^2=2px\) και η έλλειψη \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1\).
α) Αν η παραβολή διέρχεται από το σημείο \(Α(1,2)\), να βρείτε:
i. Την εξίσωση της παραβολής.
(Μονάδες 10)
ii. Την εστία \(Ε\) της παραβολής.
(Μονάδες 5)
β) Να βρεθεί η εξίσωση της έλλειψης με κέντρο το \(Ο\), αν η μια εστία της είναι το σημείο \(Ε(1,0)\) και ο μεγάλος άξονας της έχει μήκος ίσο με \(4\).
(Μονάδες 10)
Απάντηση Θέματος: 22168
α) i. Η παραβολή \(y^2=2px\) διέρχεται από το \(Α(1,2)\), οπότε οι συντεταγμένες του σημείου \(Α\) επαληθεύουν την εξίσωσή της, δηλαδή
$$2^2=2p\cdot 1\iff 4=2p\iff p=2.$$
Επομένως,
$$y^2=2\cdot 2x\iff y^2=4x.$$
ii. Η εστία \(Ε\) της παραβολής είναι \(Ε\left(\dfrac{p}{2},0\right)\), δηλαδή \(Ε(1,0)\).
β) Μία από τις εστίες της έλλειψης είναι το σημείο \(Ε(γ,0)\) και ο μεγάλος άξονας έχει μήκος \(2α\). Αφού η εστία είναι το σημείο \(Ε(1,0)\), έχουμε ότι \(γ=1\). Επειδή ο μεγάλος άξονας έχει μήκος ίσο με \(4\), έχουμε ότι \(2α=4\), οπότε \(α=2\). Είναι
\begin{align}β^2&=α^2-γ^2\\ &=2^2-1^2\\ &=4-1\\ &=3.\end{align}
Οπότε, η εξίσωση της έλλειψης γίνεται
$$\frac{x^2}{2^2}+\frac{y^2}{3}=1\iff\frac{x^2}{4}+\frac{y^2}{3}=1.$$
Θέμα: 22192
ΘΕΜΑ 2
Δίνεται η έλλειψη \((C)\) με εξίσωση:
$$\frac{x^2}{225}+\frac{y^2}{81}=1\quad(1)$$
α) Να βρείτε τις συντεταγμένες των εστιών \(Ε\) και \(Ε'\).
(Μονάδες 10)
β) Να αποδείξετε ότι το σημείο \(Β(0,9)\) είναι σημείο της έλλειψης.
(Μονάδες 5)
γ) Να βρείτε την εξίσωση της εφαπτομένης έλλειψης στο σημείο της \(Β(0,9)\).
(Μονάδες 10)
Απάντηση Θέματος: 22192
α) Η έλλειψη με εξίσωση την \((1)\) έχει \(α^2=225\), \(β^2=81\) και εστίες τα σημεία \(Ε(γ,0)\), \(Ε'(-γ,0)\). Είναι
$$γ^2=α^2-β^2=225-81=144.$$
Άρα, \(γ=12\). Επομένως, οι εστίες της έλλειψης είναι \(Ε(12,0)\) και \(Ε'(-12,0)\).
β) Εξετάζουμε αν οι συντεταγμένες του σημείου \(Β\) επαληθεύουν την εξίσωση της έλλειψης. Για \(x=0\) και \(y=9\) είναι
$$\frac{0^2}{225}+\frac{9^2}{81}=1.$$
Η τελευταία ισότητα είναι αληθής, οπότε το σημείο \(Β\) είναι σημείο της έλλειψης.
γ) Η εξίσωση της εφαπτομένης της έλλειψης στο σημείο της \(B(x_1,y_1)\) είναι
$$\frac{xx_1}{225}+\frac{yy_1}{81}=1.$$
Αφού δίνεται ότι \(B(0,9)\), η ζητούμενη εξίσωση θα είναι
$$\frac{0x}{225}+\frac{9y}{81}=1\iff y=9.$$
Η καμπύλη της έλλειψης, οι εστίες \(Ε\), \(Ε'\) της, και η εφαπτομένη \((ε)\) απεικονίζονται στο ακόλουθο σχήμα:
Θέμα: 22268
ΘΕΜΑ 2
Δίνεται η εξίσωση:
$$\frac{x^2}{9}+\frac{y^2}{4}=1\quad(1)$$
α) Να γράψετε στο τετράδιό σας συμπληρωμένη την παρακάτω πρόταση: «Τα σημεία του επιπέδου που επαληθεύουν την εξίσωση \((1)\) βρίσκονται σε μια καμπύλη που ονομάζεται ……………….. Οι εστίες της, \(Ε\) και \(Ε'\), έχουν συντεταγμένες \(Ε(\dots,\dots)\) και \(Ε'(\dots,\dots)\). Το μήκος του μεγάλου άξονα είναι ίσο με ….. και η εκκεντρότητα της είναι ίση με ………».
(Μονάδες 15)
β) Να βρείτε την εξίσωση της ευθείας \((ε)\) η οποία εφάπτεται στην καμπύλη που περιγράφει η εξίσωση \((1)\), στο σημείο της \(Β(0,-2)\).
(Μονάδες 10)
Απάντηση Θέματος: 22268
Η εξίσωση \((1)\) είναι της μορφής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1\), όπου \(α^2=9\) και \(β^2=4\). Η εξίσωση αυτής της μορφής παριστάνει τα σημεία του επιπέδου που βρίσκονται σε έλλειψη με εστίες στον άξονα \(x'x\). Οι εστίες έχουν συντεταγμένες \(Ε(γ,0)\) και \(Ε'(-γ, 0)\), όπου \(γ=\sqrt{α^2-β^2}=\sqrt{5}\). Η εκκεντρότητα της έλλειψης είναι \(ε=\dfrac{γ}{α}=\dfrac{\sqrt{5}}{3}\). Το μήκος του μεγάλου άξονα της έλλειψης είναι ίσο με \(2α=2\cdot 3 =6\).
α) «Τα σημεία του επιπέδου που επαληθεύουν την εξίσωση \((1)\) βρίσκονται σε μια καμπύλη που ονομάζεται έλλειψη. Οι εστίες της, \(Ε\) και \(Ε'\), έχουν συντεταγμένες \(Ε(\sqrt{5},0)\) και \(Ε'(-\sqrt{5},0)\). Το μήκος του μεγάλου άξονα είναι ίσο με \(6\) και η εκκεντρότητα της είναι ίση με \(\dfrac{\sqrt{5}}{3}\) ».
β)
Η εφαπτόμενη ευθεία σε σημείο με συντεταγμένες \((x_1, y_1)\) της έλλειψης είναι της μορφής
$$\frac{xx_1}{9}+\frac{yy_1}{4}=1\iff 4xx_1+9yy_1=36.$$
Δίνεται το σημείο επαφής \(Β(0,-2)\), οπότε η ζητούμενη ευθεία \((ε)\) θα έχει εξίσωση
\begin{align}&4x\cdot 0+9y\cdot(-2)=36\\ \iff& -18y=36\\ \iff& y=-2.\end{align}
Θέμα: 22556
ΘΕΜΑ 2
Η έλλειψη του παρακάτω σχήματος έχει κορυφές τα σημεία \(Α'(-5,0)\), \(Α(5,0)\), \(Β'(0,-4)\) και \(Β(0,4).\)
α) Να αποδείξετε ότι:
i. Τα μήκη των αξόνων της έλλειψης είναι \((A'A)=10\) και \((B'B)=8.\)
(Μονάδες 10)
ii. Οι εστίες της έλλειψης είναι τα σημεία \(E'(-3,0)\) και \(E(3,0).\)
(Μονάδες 10)
β) Έστω \(M\) ένα σημείο της έλλειψης. Να αποδείξετε ότι \((ME')+(ME)=10.\)
(Μονάδες 5)
Απάντηση Θέματος: 22556
α) i. Είναι
$$(A'A)=|x_A-x_{A'}|=|5+5|=10$$
και
$$(B'B)=|y_B-y_{B'}|=|4+4|=8,$$
άρα ο μεγάλος άξονας έχει μήκος \((A'A)=10\) και ο μικρός άξονας έχει μήκος \((B'B)=8.\)
ii. Είναι
$$(A'A)=2α\iff 2α=10\iff α=5$$
και
$$(B'B)=2β\iff 2β=8\iff β=4.$$
Επομένως
\begin{align}&α^2=β^2+γ^2\\ \iff&5^2=4^2+γ^2\\ \iff&γ^2=9\\ \iff&γ=3.\end{align}
Άρα οι εστίες της έλλειψης είναι τα σημεία \(E'(-3,0)\) και \(E(3,0).\)
β) Επειδή το \(M\) είναι σημείο της έλλειψης, σύμφωνα με τον ορισμό της έλλειψης θα είναι
$$(ME')+(ME)=2α$$ $$\iff (ME')+(ME)=10.$$
Θέμα: 22558
ΘΕΜΑ 2
Η έλλειψη του παρακάτω σχήματος έχει εστίες τα σημεία \(E'(-2,0)\) και \(E(2,0)\) και μήκος μεγάλου άξονα \((A'A)=8.\)
α) Να αποδείξετε ότι η έλλειψη έχει εξίσωση \(\dfrac{x^2}{16}+\dfrac{y^2}{12}=1.\)
(Μονάδες 12)
β) Έστω \(Σ\) και \(Ρ\) τα σημεία της έλλειψης που έχουν την ίδια τετμημένη με την εστία \(Ε(2,0).\) Επίσης το \(Σ\) έχει θετική τεταγμένη και το \(Ρ\) αρνητική τεταγμένη.
i. Να αποδείξετε ότι \(Σ(2,3)\) και \(Ρ(2,-3).\)
(Μονάδες 8)
ii. Να βρείτε το μήκος του τμήματος \(ΣΡ.\)
(Μονάδες 5)
Απάντηση Θέματος: 22558
α) Οι εστίες της έλλειψης είναι τα σημεία \(E'(-2,0)\) και \(E(2,0),\) άρα
$$2γ=(Ε'Ε)=4\iff γ=2.$$
Το μήκος του μεγάλου άξονα είναι \((A'A)=8,\) άρα
$$2α=(Α'Α)=8\iff α=4.$$
Επομένως
$$β^2=α^2-γ^2=4^2-2^2=12.$$
Επειδή οι εστίες βρίσκονται στον άξονα \(x'x,\) η έλλειψη έχει εξίσωση της μορφής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1,\) οπότε με αντικατάσταση προκύπτει \(\dfrac{x^2}{16}+\dfrac{y^2}{12}=1.\)
β) i. Από την εξίσωση της έλλειψης \(\dfrac{x^2}{16}+\dfrac{y^2}{12}=1,\) για \(x=x_E=2\) βρίσκουμε
\begin{align}&\frac{2^2}{16}+\frac{y^2}{12}=1\\ \iff&\frac{1}{4}+\frac{y^2}{12}=1\\ \iff&3+y^2=12\\ \iff&y^2=9\\ \iff&y=\pm3.\end{align}
Επειδή το \(Σ\) έχει θετική τεταγμένη και το \(Ρ\) αρνητική, θα είναι \(Σ(2,3)\) και \(Ρ(2,-3).\)
ii. Είναι
\begin{align}(ΣΡ)&=|y_Ρ-y_Σ|\\ &=|-3-3|\\ &=|-6|\\ &=6.\end{align}
Θέμα: 22564
ΘΕΜΑ 2
Δίνονται οι ελλείψεις \((C_1):\ \dfrac{x^2}{12}+\dfrac{y^2}{6}=1\) και \((C_2):\ \dfrac{x^2}{6}+\dfrac{y^2}{12}=1.\)
α) Να αποδείξετε ότι τα σημεία \(Α(2,2)\) και \(Β(-2,2)\) ανήκουν και στις δύο ελλείψεις.
(Μονάδες 10)
β) Να αποδείξετε ότι η εξίσωση της εφαπτομένης \((ε_1)\) της έλλειψης \(C_1\) στο σημείο \(Α\), και η εξίσωση της εφαπτομένης \(ε_2\) της έλλειψης \((C_2)\) στο σημείο \(Β\) είναι αντίστοιχα \(x+2y-6=0\) και \(-2x+y-6=0.\)
(Μονάδες 10)
γ) Να αποδείξετε ότι οι εφαπτομένες \((ε_1),\) \((ε_2)\) είναι κάθετες.
(Μονάδες 5)
Απάντηση Θέματος: 22564
α) Οι συντεταγμένες του σημείου \(Α\) επαληθεύουν τις εξισώσεις των δύο ελλείψεων αφού
$$\frac{2^2}{12}+\frac{2^2}{6}=\frac{4}{12}+\frac{4}{6}=\frac{2}{3}+\frac{1}{3}=1$$
και
$$\frac{2^2}{6}+\frac{2^2}{12}=\frac{4}{6}+\frac{4}{12}=\frac{1}{3}+\frac{2}{3}=1.$$
Το σημείο \(Β\) είναι συμμετρικό του σημείο \(Α\) ως προς τον άξονα \(y'y,\) επομένως επίσης θα ανήκει στις δύο ελλείψεις.
β) Η εφαπτομένη \((ε_1)\) της έλλειψης \((C_1)\) στο σημείο \(Α\) έχει εξίσωση
\begin{align}&\frac{2x}{12}+\frac{2y}{6}=1\\ \iff&\frac{x}{6}+\frac{2y}{6}=1\\ \iff&x+2y=6\\ \iff&x+2y-6=0.\end{align}
Αντίστοιχα, η εφαπτομένη \((ε_2)\) της έλλειψης \((C_2)\) στο σημείο \(Β\) έχει εξίσωση
\begin{align}&\frac{-2x}{6}+\frac{2y}{12}=1\\ \iff&\frac{-2x}{6}+\frac{y}{6}=1\\ \iff&-2x+y=6\\ \iff&-2x+y-6=0.\end{align}
γ) Ο συντελεστής διεύθυνσης της εφαπτομένης \((ε_1)\) είναι \(λ_1=-\dfrac{1}{2}\) και ο συντελεστής διεύθυνσης της εφαπτομένης \((ε_2)\) είναι \(λ_2=2.\) Οι εφαπτομένες \((ε_1),\) \((ε_2)\) είναι κάθετες, εφόσον
$$λ_1λ_2=-\frac{1}{2}\cdot2=-1.$$
Κ34
Θέμα: 16128
ΘΕΜΑ 2
Δίνεται η υπερβολή
$$(𝐶): \dfrac{𝑥^2}{16}−\dfrac{𝑦^2}{9}=1.$$
α) Να βρείτε τις συντεταγμένες των εστιών \(𝛦'\) και \(𝛦.\)
(Μονάδες 10)
β) Αν το \(𝑁\) είναι τυχαίο σημείο της \((𝐶)\), να βρείτε την τιμή της διαφοράς \(|(𝛮𝛦')−(𝛮𝛦)|.\)
(Μονάδες 5)
γ) Να σχεδιάσετε την υπερβολή \((𝐶).\)
(Μονάδες 10)
Απάντηση Θέματος: 16128
α) Καθώς η υπερβολή έχει εξίσωση της μορφής \(\dfrac{𝑥^2}{𝛼^2}−\dfrac{𝑦^2}{𝛽^2}=1\), θα είναι \(𝛼^2=16\) και \(𝛽^2=9\), οπότε \(𝛾^2=𝛼^2+𝛽^2=25\), άρα \(𝛾=5.\)
Έτσι, οι εστίες είναι τα σημεία \(𝛦'(−5,0)\) και \(𝛦(5,0).\)
β) Από τον ορισμό της υπερβολής γνωρίζουμε ότι η απόλυτη τιμή της διαφοράς των αποστάσεων ενός σημείου της υπερβολής από τις εστίες ισούται με \(2𝛼.\) Έτσι, θα έχουμε ότι
$$|(𝛮𝛦')−(𝛮𝛦)|=2\cdot 4=8.$$
γ) Γνωρίζουμε ότι η υπερβολή \(\dfrac{𝑥^2}{𝛼^2}−\dfrac{𝑦^2}{𝛽^2}=1\) τέμνει τον άξονα \(𝑥'𝑥\) στα σημεία \((−𝛼,0)\) και \((𝛼,0)\), δηλαδή στα σημεία \((−4,0)\) και \((4,0).\) Επίσης, δεν τέμνει τον άξονα \(y'y\), αφού αν αυτό συνέβαινε θα είχαμε \(0−\dfrac{𝑦^2}{𝛽^2}=1\), αδύνατο. Έτσι, έχουμε το παρακάτω σχήμα.
Θέμα: 17944
ΘΕΜΑ 3
Δίνεται η υπερβολή με εξίσωση της μορφής
$$C:\frac{x^2}{a^2}-\frac{y^2}{β^2}=1,$$
εστιακή απόσταση \(ΕΕ'=2\sqrt{7}\) και εκκεντρότητα \(ε=\dfrac{\sqrt{7}}{2}\).
α) Να αποδείξετε ότι \(α=2\), \(β=\sqrt{3}\).
(Μονάδες 8)
β) i. Να βρείτε τις συντεταγμένες των κορυφών \(A\), \(A'\) της υπερβολής \((C)\).
ii. Να βρείτε τις εξισώσεις των ασύμπτωτων ευθειών της υπερβολής \((C)\).
(Μονάδες 8)
γ) Να σχεδιάσετε στο ίδιο σύστημα αξόνων την υπερβολή \((C)\), τις ασύμπτωτές της, τις εστίες της και τις κορυφές της.
(Μονάδες 9)
Απάντηση Θέματος: 17944
α) Ισχύει ότι η εστιακή απόσταση είναι
$$2γ=2\sqrt{7}\iff γ=\sqrt{7}.$$
Για την εκκεντρότητα της υπερβολής ισχύει ότι
\begin{align}&ε=\frac{γ}{α}\\ \iff&\frac{\sqrt{7}}{2}=\frac{\sqrt{7}}{a}\\ \iff& α=2.\end{align}
Για τους συντελεστές \(α\), \(β\) ισχύει ότι
\begin{align}β^2&=γ^2-α^2\\ &=\sqrt{7}^2-2^2\\ &=3,\end{align}
άρα \(β=\sqrt{3}\).
β) i. Οι κορυφές της υπερβολής έχουν συντεταγμένες \(Α(α,0)\), \(Α'(-α,0)\), άρα θα είναι οι \(Α(2,0)\), \(Α'(-2,0)\).
ii. Οι ασύμπτωτες της υπερβολής είναι
$$ε_1:y=-\dfrac{β}{α}x,\quad ε_2:y=\dfrac{β}{α}x$$
οπότε θα έχουμε
\begin{align}&ε_1:y=-\frac{\sqrt{3}}{2}x,\\ &ε_2:y=\frac{\sqrt{3}}{2}x.\end{align}
γ) Η γραφική παράσταση και τα υπόλοιπα στοιχεία φαίνονται στο παρακάτω σχήμα.

Θέμα: 21651
ΘΕΜΑ 2
Η υπερβολή \(C\) έχει εστίες τα σημεία \(Ε(5,0)\), \(Ε'(-5,0)\) και διέρχεται από το σημείο \(Α(4,0)\).
α) Να αποδείξετε ότι έχει εκκεντρότητα \(\dfrac{5}{4}\).
(Μονάδες 10)
β) Να βρείτε την εξίσωση της \(C\).
(Μονάδες 8)
γ) Να βρείτε την εξίσωση της εφαπτομένης της \(C\) στο σημείο της \(Μ(5,\dfrac{9}{4})\).
(Μονάδες 7)
Απάντηση Θέματος: 21651
ΛΥΣΗ
α) Η \(C\) έχει εστίες τα σημεία \(Ε(5,0)\), \(Ε'(-5,0)\) οπότε έχει εξίσωση της μορφής \(\dfrac{x^{2}}{α^{2}}-\dfrac{y^{2}}{β^{2}}=1\) και \(γ=5\). Αφού διέρχεται από το σημείο \(Α(4,0)\) έχουμε ότι:
$$\dfrac{4^{2}}{α^{2}}-\dfrac{0^{2}}{β^{2}}=1$$ $$\Leftrightarrow \dfrac{16}{α^{2}}=1$$ $$\Leftrightarrow α^{2}=16$$
και επειδή \(α>0\) έχουμε τελικά ότι \(α=4\). Συνεπώς έχει εκκεντρότητα:
$$ε=\dfrac{γ}{α}=\dfrac{5}{4}$$
β) Από τη σχέση \(γ^{2}=α^{2}+β^{2}\) έχουμε ότι:
$$5^{2}=4^{2}+β^{2}$$ $$\Leftrightarrow β^{2}=9$$
και επειδή \(β>0\) έχουμε \(β=3\).
Τελικά η ζητούμενη εξίσωση είναι η:
$$\dfrac{x^{2}}{16}-\dfrac{y^{2}}{9}=1$$
γ) Η εφαπτόμενη στο \(Μ(5,\dfrac{9}{4})\) έχει εξίσωση:
$$\dfrac{5⋅x}{16}-\dfrac{\dfrac{9}{4}⋅y}{9}=1$$ $$\Leftrightarrow \dfrac{5x}{16}-\dfrac{y}{4}=1$$
Θέμα: 21973
ΘΕΜΑ 1
α) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στην κόλλα σας δίπλα στον αριθμό που αντιστοιχεί σε κάθε πρόταση τη λέξη ΣΩΣΤΟ, αν η πρόταση είναι σωστή ή ΛΑΘΟΣ, αν η πρόταση είναι λανθασμένη.
i. Αν ισχύει \(| \vec{α} | = λ | \vec{β} |\) τότε υποχρεωτικά \(\vec{α} \parallel \vec{β}\).
ii. Η εφαπτομένη του κύκλου \((C): x^2 + y^2 = ρ^2\) σε ένα σημείο του \(Α(x_1, y_1)\), έχει εξίσωση \(xx_1 + yy_1 = ρ^2.\)
iii. Η διευθετούσα της παραβολής \(y^2 =2px\), έχει εξίσωση \(x = - \dfrac{𝑝}{2}\).
iv. Η εκκεντρότητα μιας έλλειψης είναι μικρότερη της μονάδας.
v. Η εξίσωση: \(x^2 + y^2 = α^2\) είναι εξίσωση ισοσκελούς υπερβολής.
(Μονάδες 10)
β) Να αποδείξετε ότι η εξίσωση της ευθείας που διέρχεται από το σημείο \(Α(x_0, y_0)\) και έχει συντελεστή διεύθυνσης \(λ\) είναι \(y -y_0 = λ(x -x_0).\)
(Μονάδες 15)
Απάντηση Θέματος: 21973
Απαντήσεις
α)
- i. Λάθος
- ii. Σωστό
- iii. Σωστό
- iv. Σωστό
- v. Λάθος
β) Πρόταση σελίδα 60, 61.
Θέμα: 22169
ΘΕΜΑ 2
Δίνεται η υπερβολή \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) με ασύμπτωτη την \(y=\dfrac{3}{4}x.\) Η απόσταση των κορυφών της, \(Α\) και \(Α',\) είναι \(8\).
α) i. Να βρείτε την εξίσωση της υπερβολής.
(Μονάδες 10)
ii. Ποιες είναι οι εστίες της υπερβολής;
(Μονάδες 5)
β) Να βρείτε την εφαπτομένη της \(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1\) στο σημείο της \(\left(5,\dfrac{9}{4}\right).\)
(Μονάδες 10)
Απάντηση Θέματος: 22169
α) i. Οι ασύμπτωτες της υπερβολής είναι η \(y=\dfrac{β}{α}x\) και η \(y=-\dfrac{β}{α}x.\) Εφόσον η \(y=\dfrac{3}{4}x\) είναι ασύμπτωτη και \(α, β > 0\), έχουμε ότι
$$\frac{β}{α}=\frac{3}{4}\iff 4β=3α\iff β=\frac{3}{4}α.$$
Η απόσταση των κορυφών της \(ΑΑ'\) είναι ίση με \(2α\), οπότε
$$2α=8\iff α=4.$$
Άρα έχουμε \(β=\dfrac{3}{4}\cdot 4=3.\) Επομένως η εξίσωση της υπερβολής \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) γίνεται \(\dfrac{x^2}{4^2}-\dfrac{y^2}{3^2}=1\) ή \(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1.\)
ii. Είναι \(α^2+β^2=γ^2\) και από το (α.i) ερώτημα έχουμε ότι \(α=4\) και \(β=3\). Επομένως
$$4^2+3^2=γ^2\iff γ^2=25\overset{γ>0}{\Leftrightarrow} γ=5.$$
Οι εστίες είναι της μορφής \(Ε(γ,0)\) και \(Ε'(-γ,0)\), επομένως \(Ε(5,0)\) και \(Ε'(-5,0).\)
β) Η εφαπτόμενη της υπερβολής \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) στο σημείο της \((x_1,y_1)\) δίνεται από τον τύπο
$$\frac{xx_1}{α^2}-\frac{yy_1}{β^2}=1\iff\frac{xx_1}{16}-\frac{yy_1}{9}=1.$$
Στο σημείο \(\left(5,\dfrac{9}{4}\right)\) θα έχουμε
$$\frac{5x}{16}-\frac{\frac{9}{4}y}{9}=1\iff \frac{5x}{16}-\frac{y}{4}=1.$$
Θέμα: 22174
ΘΕΜΑ 4
Πλανήτης κινείται πάνω σε επίπεδο, ελλειπτικά γύρω από τον ήλιο του. Στο καρτεσιανό επίπεδο ο ήλιος βρίσκεται στην εστία της έλλειψης \(Ε(γ,0),\) ενώ η άλλη εστία είναι στο \(Ε'(-γ,0).\) Η εκκεντρότητα της τροχιάς είναι \(0,6\) ενώ ο μεγάλος άξονας έχει μήκος \(10.\)
α) Να βρεθεί η εξίσωση της τροχιάς.
(Μονάδες 9)
β) Θεωρούμε ότι ο πλανήτης κινείται πάνω στην \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1.\)
i. Τη στιγμή που ο πλανήτης βρίσκεται στο σημείο \(Γ\left(3,\dfrac{16}{5}\right)\), εκπέμπεται από αυτόν σήμα που κινείται κατά τη διεύθυνση της εφαπτομένης της τροχιάς του προς τη μεριά του άξονα \(Οy\). Να εξετάσετε αν αυτό το σήμα θα περάσει από το σημείο \(Δ(0,5).\)
(Μονάδες 9)
ii. Κομήτης κινείται στο ίδιο επίπεδο με τον πλανήτη και πάνω στην καμπύλη \(\dfrac{x^2}{25}-\dfrac{y^2}{16}=1\) με \(x > 0.\) Ποια είναι τα σημεία συνάντησης των δύο τροχιών;
(Μονάδες 7)
Απάντηση Θέματος: 22174
α) Ο μεγάλος άξονας της έλλειψης είναι μήκους \(2α,\) οπότε \(2α =10,\) και άρα \(α=5.\) Η εκκεντρότητα της έλλειψης είναι \(ε=\dfrac{γ}{α}\), οπότε
$$\frac{γ}{α}=0.6\iff\frac{γ}{5}=0.6\iff γ=3.$$
Όμως
$$β^2=α^2-γ^2=5^2-3^2=25-9=16,$$
άρα η εξίσωση της έλλειψης δίνεται από τον τύπο
$$\frac{x^2}{α^2}+\frac{y^2}{β^2}=1\iff\frac{x^2}{25}+\frac{y^2}{16}=1.$$
β) i. Η εφαπτομένη της έλλειψης σε σημείο \((x_1,y_1)\) δίνεται από τον τύπο \(\dfrac{xx_1}{α^2}+\dfrac{yy_1}{β^2}=1.\) Εφόσον το σημείο επαφής είναι το \(Γ\left(1,\dfrac{16}{5}\right)\), η εξίσωση της εφαπτομένης θα γίνει
$$\frac{3x}{25}+\frac{\frac{16}{5}y}{16}=1\iff\frac{3x}{25}+\frac{y}{5}=1.$$
Για να διέρχεται από το σημείο \(Δ(0,5)\) θα πρέπει οι συντεταγμένες του σημείου να την επαληθεύουν. Πράγματι,
$$\frac{3\cdot0}{25}+\frac{5}{5}=1\iff 1=1,$$
που σημαίνει ότι η εφαπτομένη διέρχεται από το σημείο \(Δ.\)
ii. Σημεία συνάντησης των τροχιών είναι οι λύσεις του συστήματος των εξισώσεών τους, εφόσον υπάρχουν. Οι εξισώσεις είναι \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\) και \(\dfrac{x^2}{25}-\dfrac{y^2}{16}=1.\) Προσθέτοντας κατά μέλη έχουμε
$$2\frac{x^2}{25}=2\iff x^2=25\overset{x>0}{\Longleftrightarrow} x=5$$
Η \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\) για \(x=5\) μας δίνει
\begin{align}&\frac{5^2}{25}+\frac{y^2}{16}=1\\ &\iff1+\frac{y^2}{16}=1\\ &\iff\frac{y^2}{16}=0\\ &\iff y=0.\end{align}
Σημείο συνάντησης είναι λοιπόν το \((5,0).\)
Θέμα: 22196
ΘΕΜΑ 2
Δίνεται η υπερβολή \((C)\) με εξίσωση:
$$x^2-y^2=25\quad(1)$$
α) Να βρείτε τις συντεταγμένες των εστιών \(Ε\) και \(Ε'\).
(Μονάδες 10)
β) Να βρείτε τις ασύμπτωτες \((ε_1)\), \((ε_2)\) της υπερβολής.
(Μονάδες 10)
γ) Τι γωνία σχηματίζουν οι ασύμπτωτες \((ε_1)\), \((ε_2)\); Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 5)
Απάντηση Θέματος: 22196
α) Η εξίσωση \((1)\) γράφεται ισοδύναμα
$$\frac{x^2}{25}-\frac{y^2}{25}=1.$$
Επομένως, είναι
\begin{align}α^2=25\iff α=5,\\ β^2=25\iff β=5\end{align}
και
$$γ^2=α^2+β^2=25+25=50.$$
Άρα, \(γ=\sqrt{50}=5\sqrt{2}\). Οι εστίες της έλλειψης είναι τα σημεία \(Ε(γ,0)\), \(Ε'(-γ,0)\), δηλαδή \(Ε(5\sqrt{2},0)\) και \(Ε'(-5\sqrt{2},0)\).
β) Οι ασύμπτωτες της υπερβολής \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) είναι οι ευθείες \((ε_1): y=\dfrac{β}{α}x\) και \((ε_2): y=-\dfrac{β}{α}x\) δηλαδή \((ε_1): y=x\) και \((ε_2): y=-x\).
γ) Οι ευθείες \((ε_1)\), \((ε_2)\) έχουν συντελεστές διεύθυνσης \(λ_1=1\) και \(λ_2=-1\) αντίστοιχα. Αφού \(λ_1λ_2=-1\), συμπεραίνουμε ότι οι ασύμπτωτες \((ε_1)\), \((ε_2)\) είναι κάθετες. Η καμπύλη της υπερβολής, οι εστίες \(Ε\), \(Ε'\) της, και οι ασύμπτωτες απεικονίζονται στο ακόλουθο σχήμα:
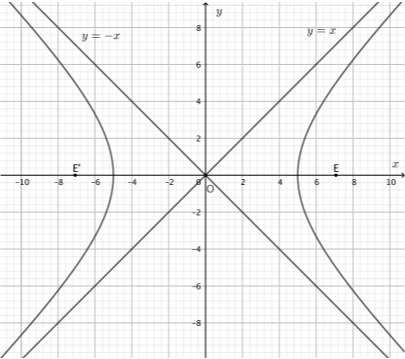
Θέμα: 22269
ΘΕΜΑ 2
Δίνεται η υπερβολή με εξίσωση:
$$\frac{x^2}{4}-y^2=1\quad(1)$$
α) Να προσδιορίσετε, δικαιολογώντας την απάντησή σας,:
i. τις συντεταγμένες των εστιών της,
ii. την εκκεντρότητά της,
iii. και τις εξισώσεις των ασύμπτωτων της υπερβολής.
(Μονάδες 15)
β) Να βρείτε την εξίσωση της ευθείας \((ε)\) που εφάπτεται στην υπερβολή στο σημείο της \(Α\left(\sqrt{5},\dfrac{1}{2}\right).\)
(Μονάδες 10)
Απάντηση Θέματος: 22269
α) Η υπερβολή με εξίσωση \(\dfrac{x^2}{4}-y^2=1\) έχει \(α^2=4\) και \(β^2=1\). Οι εστίες της βρίσκονται στον άξονα \(x'x\) και έχουν συντεταγμένες \(Ε(γ, 0)\) και \(Ε'(-γ, 0)\), όπου \(γ=\sqrt{α^2+β^2}=\sqrt{5}\).
i. Οι εστίες της υπερβολής έχουν συντεταγμένες \(Ε(\sqrt{5},0)\) και \(Ε'(-\sqrt{5},0)\).
ii. Η εκκεντρότητα της υπερβολής είναι \(ε=\dfrac{γ}{α}=\dfrac{\sqrt{5}}{2}\).
iii. Οι ασύμπτωτες της υπερβολής είναι οι \(y=\dfrac{β}{α}x=\dfrac{1}{2}x\) και \(y=-\dfrac{β}{α}x=-\dfrac{1}{2}x\).
β) Η εξίσωση της εφαπτόμενης της υπερβολής στο σημείο της με συντεταγμένες \((x_1, y_1)\) θα έχει τη μορφή
$$\frac{xx_1}{4}-yy_1=1\iff xx_1-4yy_1=4.$$
Οπότε για \(x_1=\sqrt{5}\) και \(y_1=\dfrac{1}{2}\) θα έχουμε την \((ε)\) με εξίσωση
$$\sqrt{5}x-4\frac{1}{2}y=4\iff \sqrt{5}x-2y=4.$$
Θέμα: 22559
ΘΕΜΑ 2
Η υπερβολή στο παρακάτω σχήμα έχει εστίες τα σημεία \(E'(-10,0)\) και \(E(10,0)\) και κορυφές τα σημεία \(A'(-8,0)\) και \(A(8,0).\)
α) Να αποδείξετε ότι η υπερβολή έχει εξίσωση \(\dfrac{x^2}{64}+\dfrac{y^2}{36}=1.\)
(Μονάδες 12)
β) Έστω \(M\) ένα σημείο της υπερβολής.
i. Να αποδείξετε ότι \(|(ME')-(ME)|=16.\)
(Μονάδες 8)
ii. Αν \((ME)=9,\) να βρείτε την απόσταση του σημείου \(M\) από την εστία \(E'.\)
(Μονάδες 5)
Απάντηση Θέματος: 22559
α) Επειδή η υπερβολή έχει τις εστίες της \(Ε'(-10,0),\) \(Ε(10,0)\) και τις κορυφές της \(Α'(-8,0),\) \(Α(8,0)\) στον άξονα \(x'x,\) η εξίσωση της είναι της μορφής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1.\) Είναι \(γ=10\) και \(α=8,\) άρα
\begin{align}&β^2=γ^2-α^2\\ \iff&β^2=10^2-8^2\\ \iff&β^2=36\\ \iff&β=6.\end{align}
Επομένως η υπερβολή έχει εξίσωση \(\dfrac{x^2}{64}+\dfrac{y^2}{36}=1.\)
β) i. To \(M\) είναι σημείο της υπερβολής, αν και μόνο αν η απόλυτη τιμή της διαφοράς των αποστάσεών του από τις εστίες \(Ε'\) και \(E\) είναι \(2α,\) δηλαδή \(|(ΜΕ')-(ΜΕ)|=2α.\) Επειδή \(α=8,\) θα είναι \(|(ME')-(ME)|=16.\)
ii. Δίνεται \((ME)=9\), οπότε έχουμε
\begin{align}&|(ME')-9|=16\\ \iff&(ME')-9=\pm16\\ \iff&(ME')=-7\text{ ή }(ME')=25,\end{align}
και επειδή \((ME')>0\), θα είναι \((ME')=25.\)
Θέμα: 22561
ΘΕΜΑ 2
Στο παρακάτω σχήμα η υπερβολή \(C\) έχει εξίσωση \(x^2-y^2=9,\) οι ευθείες \((δ_1)\) και \((δ_2)\) είναι οι ασύμπτωτές της, και η \((ε)\) είναι η εφαπτομένη της στo σημείο της \(Μ(5,4).\)
α) Να αποδείξετε ότι:
i. Οι εξισώσεις των ασυμπτώτων είναι \((δ_1):\ y=x\) και \((δ_2):\ y=-x.\)
(Μονάδες 8)
ii. Η εξίσωση της εφαπτομένης στο \(M\) είναι \((ε):\ 5x-4y=9.\)
(Μονάδες 8)
β) Να βρείτε τις συντεταγμένες του σημείου τομής των ευθειών \((ε)\) και \((δ_1),\) καθώς και τις συντεταγμένες του σημείου τομής των ευθειών \((ε)\) και \((δ_2).\)
(Μονάδες 9)
Απάντηση Θέματος: 22561
α) i. Οι ασύμπτωτες της υπερβολής \(\dfrac{x^2}{α^2}+\dfrac{y^2}{β^2}=1\) είναι οι ευθείες \(y=\dfrac{β}{α}x\) και \(y=-\dfrac{β}{α}x.\)
Επειδή \((C):\ x^2-y^2=9\), είναι \(α^2=β^2=9,\) άρα \(α=β=3,\) οπότε οι ασύμπτωτες της \((C)\) είναι οι ευθείες \((δ_1):\ y=\dfrac{3}{3}x=x\) και \(δ_2:y=-\dfrac{3}{3}x=-x.\)
ii. H εφαπτομένη \(ε\) της υπερβολής \((C):\ x^2-y^2=9\) στο σημείο της \(M(5,4)\) έχει εξίσωση
$$xx_1-yy_1=9\iff5x-4y=9.$$
β) Τα σημεία τομής της \((ε):\ 5x-4y=9\) με τις \((δ_1):\ y=x\) και \((δ_2):\ y=-x\) προκύπτουν από τη λύση του συστήματος των εξισώσεών τους.
Επομένως θα έχουμε
\begin{align}&\begin{cases}5x-4y=9\\y=x\end{cases}\\ \iff&\begin{cases}5x-4x=9\\y=x\end{cases}\\ \iff&\begin{cases}x=9\\y=9\end{cases}\end{align}
και
\begin{align}&\begin{cases}5x-4y=9\\y=-x\end{cases}\\ \iff&\begin{cases}5x+4x=9\\y=-x\end{cases}\\ \iff&\begin{cases}9x=9\\y=-x\end{cases}\\ \iff&\begin{cases}x=1\\y=-1\end{cases}.\end{align}
Επομένως το σημείο τομής των \((ε)\) και \((δ_1)\) έχει συντεταγμένες \((9,9)\) και το σημείο τομής των \((ε)\) και \((δ_2)\) έχει συντεταγμένες \((1,-1).\)
Θέμα: 22567
ΘΕΜΑ 2
Στο καρτεσιανό επίπεδο \(Oxy\) η υπερβολή \((C):\ \dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) τέμνει τον άξονα \(x'x\) στα σημεία \(A'(-4,0)\) και \(A(4,0)\) και έχει ασύμπτωτες τις ευθείες \(y=\dfrac{3}{4}x\) και \(y=-\dfrac{3}{4}x.\)
α) Να αποδείξετε ότι:
i. \(α=4\) και \(β=3.\)
(Μονάδες 10)
ii. Οι εστίες της \((C)\) είναι τα σημεία \(E'(-5,0)\) και \(E(5,0).\)
(Μονάδες 10)
β) Να σχεδιάσετε το παρακάτω σχήμα, συμπληρώνοντάς το με την παραπάνω υπερβολή \((C).\)
(Μονάδες 5)
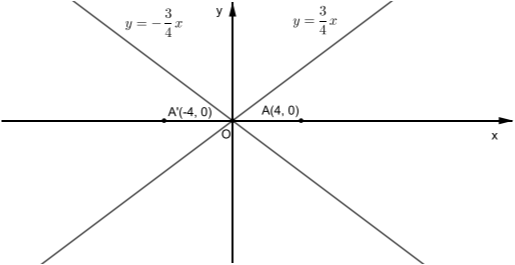
Απάντηση Θέματος: 22567
α) i. Η υπερβολή με εξίσωση \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) τέμνει τον άξονα \(x'x\) στα σημεία \(A'(-α,0)\) και \(Α(α,0).\) Δίνεται \(A'(-4,0)\) και \(A(4,0),\) άρα θα έχουμε \(α=4.\)
Οι ασύμπτωτες της υπερβολής \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) είναι οι ευθείες \(y=\dfrac{β}{α}x\) και \(y=-\dfrac{β}{α}x.\) Δίνεται ότι οι ασύμπτωτες της υπερβολής είναι οι ευθείες \(y=\dfrac{3}{4}x\) και \(y=-\dfrac{3}{4}x,\) άρα θα έχουμε \(\dfrac{β}{α}=\dfrac{3}{4}\), και επειδή \(α=4,\) προκύπτει \(β=3.\)
ii. Οι εστίες της υπερβολής \(\dfrac{x^2}{α^2}-\dfrac{y^2}{β^2}=1\) είναι τα σημεία \(E'(-γ,0)\) και \(Ε(γ,0)\), \((γ\gt0)\). Είναι
\begin{align}&γ^2=α^2+β^2\\ \iff&γ^2=4^2+3^2\\ \iff&γ^2=25\\ \iff&γ=5.\end{align}
Επομένως οι εστίες της υπερβολής είναι τα σημεία \(E'(-5,0)\) και \(E(5,0).\)
β)
3.5 Η ΕΞΙΣΩΣΗ Ax2 + By2 + Γx + Δy + E
Θέμα: 21657
ΘΕΜΑ 4
Έστω υπερβολή \(C\) με κέντρο το \((0,0)\), εστίες πάνω στον άξονα \(xx'\) της οποίας το ορθογώνιο βάσης είναι τετράγωνο.
α) Να βρείτε:
-
τις εξισώσεις των ασυμπτώτων της \(C\).
(Μονάδες 6) -
την εκκεντρότητα της \(C\).
(Μονάδες 6)
β) Αν η υπερβολή διέρχεται από το σημείο \((2,0)\) και \((ζ)\) τυχαίαευθεία παράλληλη σε κάποια εκ των ασύμπτωτων της \(C\) (που δεν ταυτίζεται με κάποια από αυτές),
-
να δείξετε ότι η \((ζ)\) έχει ένα μόνο κοινό σημείο με την \(C\).
(Μονάδες 8) -
είναι η ευθεία \((ζ)\) εφαπτόμενη της \(C\); Αιτιολογείστε την απάντησή σας.
(Μονάδες 5)
Απάντηση Θέματος: 21657
ΛΥΣΗ
α) Η υπερβολή \(C\) έχει κέντρο το \((0,0)\) και εστίες στον άξονα \(xx'\), οπότε θα έχει ασύμπτωτες της μορφής \(y=\dfrac{β}{α}x , y=-\dfrac{β}{α}x\). Αφού το ορθογώνιο βάσης είναι τετράγωνο, συμπεραίνουμε ότι \(α=β\) δηλαδή είναι ισοσκελής υπερβολή. Συνεπώς:
- οι εξισώσεις των ασυμπτώτων της υπερβολής \(C\) είναι \(y=x,y=-x\).
- για την εκκεντρότητα \(ε\) της \(C\) ισχύει ότι \(ε^{2}=1+(\dfrac{β}{α})^{2}=1+1=2\) και επειδή \(ε>0\) έχουμε τελικά ότι \(ε=\sqrt{2}\).
β) Αφού η \((ζ)\) είναι παράλληλη σε κάποια εκ των ασύμπτωτων της \(C\), θα έχει εξίσωση της μορφής \(y=x+κ\) ή \(y=-x+κ\) με \(κ≠0\). Η ισοσκελής υπερβολή \(C\) θα έχει εξίσωση της μορφής \(x^{2}-y^{2}=α^{2}\). Αφού διέρχεται από το σημείο \((2,0)\) έχουμε ότι:
$$2^{2}-0^{2}=α^{2}$$ $$\Leftrightarrow 4=α^{2}$$ $$\overset{α>0}{\Leftrightarrow }α=2$$
Το πλήθος των κοινών σημείων της \(C\) και της ευθείας \((ζ)\) είναι ίδιο με το πλήθος των λύσεων καθενός από τα συστήματα \(\begin{cases}x^{2} - y^{2} =4 \\ y=x+κ\end{cases}\) και \(\begin{cases}x^{2} - y^{2} =4 \\ y= - x+κ\end{cases}\).
Λύνουμε το 1ο σύστημα με αντικατάσταση της 2ης εξίσωσης στην 1η και έχουμε:
$$x^{2}-(x+κ)^{2}=4$$ $$\Leftrightarrow x^{2}-x^{2}-2xκ-κ^{2}=4$$ $$\Leftrightarrow -2xκ=4+κ^{2}$$ $$\overset{κ≠0}{\Leftrightarrow }x=-\dfrac{4+κ^{2}}{2κ}$$
και από τη 2η εξίσωση έχουμε ότι:
$$y=-\dfrac{4+κ^{2}}{2κ}+κ$$
Ομοίως λύνουμε το 2ο σύστημα με αντικατάσταση της 2ης εξίσωσης στην 1η και έχουμε:
$$x^{2}-(-x+κ)^{2}=4$$ $$\Leftrightarrow x^{2}-x^{2}+2xκ-κ^{2}=4$$ $$\Leftrightarrow 2xκ=4+κ^{2}$$ $$\overset{κ≠0}{\Leftrightarrow }x=\dfrac{4+κ^{2}}{2κ}$$
και από τη 2η εξίσωση έχουμε ότι:
$$y=-\dfrac{4+κ^{2}}{2κ}+κ$$
-
Σε κάθε περίπτωση το σύστημα έχει μοναδική λύση που σημαίνει ότι η \((ζ)\) έχει ένα μόνο κοινό σημείο με την \(C\).
-
Επειδή σε κάθε περίπτωση η μοναδική λύση του συστήματος προέκυψε από εξίσωση 1ου βαθμού και όχι από 2ου με διακρίνουσα \(0\), η ευθεία \((ζ)\) δεν είναι εφαπτόμενη της \(C\). Απλά την τέμνει σε ένα σημείο χωρίς όμως το σημείο αυτό να είναι σημείο επαφής. Δηλαδή η \((ζ)\) διαπερνά τη \(C\).
Σημείωση: το παραπάνω συμπέρασμα ισχύει για κάθε υπερβολή και ευθεία παράλληλη σε κάποια από τις ασύμπτωτες και όχι μόνο για τις ισοσκελείς.
