Μάθημα : Β΄ΛΥΚΕΙΟΥ - ΜΑΘΗΜΑΤΙΚΑ ΠΡ. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
Κωδικός : G217111
G217111 - ΧΡΗΣΤΟΣ ΤΡΙΑΝΤΗΣ
Ενότητες μαθήματος - Κεφάλαιο 1ο: ΔΙΑΝΥΣΜΑΤΑ - Λυμένα θέματα από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
Κεφάλαιο 1ο: ΔΙΑΝΥΣΜΑΤΑ - Λυμένα θέματα από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
Θέματα με απαντήσεις από την ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ του ΙΕΠ
Θέμα: 16147 (ΘΕΜΑ 2ο)
Δίνονται διανύσματα:
$$\vec{α}=3\vec{i}+3\sqrt{3}\ \vec{j},\ \vec{β}=\sqrt{2}\ \vec{i},\ \vec{γ}=-3\vec{j}\text{ και }\vec{δ}=(-1,1).$$
α) Να βρείτε το συντελεστή διεύθυνσης καθενός από τα διανύσματα \(\vec{α},\vec{β},\vec{δ}\).
(Μονάδες 9)
β) Να γράψετε τη γωνία που σχηματίζει καθένα από τα διανύσματα \(\vec{α},\vec{β},\vec{γ}\) και \(\vec{δ}\) με το θετικό ημιάξονα \(Ox\).
(Μονάδες 10)
γ) Να βρείτε τα μέτρα των διανυσμάτων \(\vec{α}\) και \(\vec{γ}\).
(Μονάδες 6)
Απάντηση
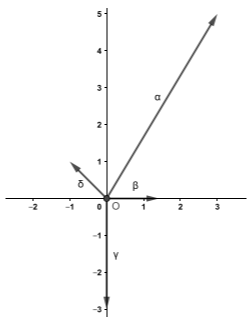
Τα διανύσματα που δίνονται έχουν συντεταγμένες:
$$\vec{α}=(3, 3\sqrt{3})$$ $$\vec{β}=(\sqrt{2}, 0)$$ $$\vec{γ}=(0 ,-3)$$ $$\text{ και } \vec{δ}=(-1, 1)$$
α) Ο συντελεστής διεύθυνσης διανύσματος, όταν η τετμημένη του δεν είναι μηδέν, ορίζεται ως το πηλίκο τεταγμένη του διανύσματος προς τετμημένη του διανύσματος. Οπότε
$$λ_\vec{α}=\frac{3\sqrt{3}}{3}=\sqrt{3}$$ $$λ_\vec{β}=\frac{0}{\sqrt{2}}=0$$ $$λ_\vec{δ}=\frac{1}{-1}=-1.$$
β) Γνωρίζουμε ότι η εφαπτομένη της γωνίας που σχηματίζει ένα διάνυσμα με το θετικό ημιάξονα \(Οx\) ισούται με το συντελεστή διεύθυνσης του διανύσματος. Αν \(ω\) είναι η γωνία που σχηματίζει το διάνυσμα \(\vec{α}\) με το θετικό ημιάξονα \(Οx\), επειδή \(λ_\vec{α}=\sqrt{3}\) (από ερώτημα (α)), θα ισχύει \(εφω = \sqrt{3}\). Επιπλέον το πέρας του διανύσματος βρίσκεται στο \(1^ο\) τεταρτημόριο, αφού έχει θετικές συντεταγμένες, άρα \(ω=60^ο\).
Το διάνυσμα \(\vec{β}=(\sqrt{2}, 0)\) έχει τεταγμένη \(0\), άρα \(\vec{β}//x'x\), και επειδή το \(\vec{β}\) έχει θετική τετμημένη σχηματίζει με το θετικό ημιάξονα \(Οx\) γωνία \(0^ο\).
Το διάνυσμα \(\vec{δ}=(0, -3)\) έχει τετμημένη \(0\), άρα \(\vec{γ}//y'y\), και επειδή το \(\vec{γ}\) έχει αρνητική τεταγμένη σχηματίζει με το θετικό ημιάξονα \(Οx\) γωνία \(270^ο\).
Αν \(φ\) είναι η γωνία που σχηματίζει το διάνυσμα \(\vec{δ}\) με το θετικό ημιάξονα \(Οx\), επειδή \(λ_\vec{δ}=-1\) (από ερώτημα (α)), θα ισχύει \(εφφ=-1\). Επιπλέον το διάνυσμα έχει αρνητική τετμημένη και θετική τεταγμένη, οπότε το πέρας του βρίσκεται στο \(2^ο\) τεταρτημόριο, άρα \(φ=135^ο\).
γ) Είναι:
$$|\vec{α}|=\sqrt{3^2+(3\sqrt{3})^2}=\sqrt{36}=6$$ $$|\vec{γ}|=\sqrt{0^2+(-3)^2}=3$$
Θέμα: 17070 (ΘΕΜΑ 2ο)
Στο καρτεσιανό επίπεδο \(Oxy\) δίνονται τα σημεία \(A(3,4)\), \(B(2,1)\), \(Γ(3,-1)\) και \(Δ(4,2)\).
α) Να σχεδιάσετε τα παραπάνω σημεία \(A\), \(B\), \(Γ\) και \(Δ\).
(Μονάδες 8)
β) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{ΔΓ}\).
(Μονάδες 9)
γ) Να αποδείξετε ότι το τετράπλευρο \(ΑΒΓΔ\) είναι παραλληλόγραμμο.
(Μονάδες 8)
Απάντηση
α)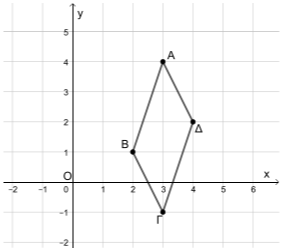
β) Είναι \(A(3,4)\), \(B(2,1)\), \(Γ(3,-1)\) και \(Δ(4,2)\), οπότε οι συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{ΔΓ}\) θα είναι
\begin{align}\overrightarrow{ΑΒ}&=(x_B-x_A,y_B-y_A)\\ &=(2-3,1-4)\\ &=(-1,-3),\\ \overrightarrow{ΔΓ}&=(x_Γ-x_Δ,y_Γ-y_Δ)\\ &=(3-4,-1-2)\\ &=(-1,-3).\end{align}
γ) Από το προηγούμενο ερώτημα προκύπτει ότι \(\overrightarrow{ΑΒ}=\overrightarrow{ΔΓ}\). Άρα τα διανύσματα \(\overrightarrow{AB}\) και \(\overrightarrow{ΔΓ}\) θα έχουν ίσα μέτρα και θα είναι παράλληλα χωρίς να συμπίπτουν. Επομένως οι πλευρές \(AB\) και \(ΔΓ\) του τετραπλεύρου \(ΑΒΓΔ\) θα είναι ίσες και παράλληλες, οπότε το τετράπλευρο \(ΑΒΓΔ\) είναι παραλληλόγραμμο.
Θέμα: 22557 (ΘΕΜΑ 2ο)
Το ισοσκελές τρίγωνο \(ABΓ\) έχει βάση \(ΒΓ\) και ύψος \(ΑΟ.\) Η κορυφή \(Α\) είναι σημείο του θετικού ημιάξονα \(Oy\) και οι κορυφές \(B\) και \(Γ\) είναι σημεία του άξονα \(x'x,\) όπως φαίνεται στο παρακάτω σχήμα. Έστω \((BΓ)=12,\) \((AO)=8\) και \(M\) το μέσο της πλευράς \(AΓ.\)
α) Να αποδείξετε ότι:
i. \(A(0,8),\) \(B(-6,0)\) και \(Γ(6,0).\)
(Μονάδες 9)
ii. \(M(3,4).\)
(Μονάδες 9)
β) Να βρείτε το μήκος της διαμέσου \(BM.\)
(Μονάδες 7)
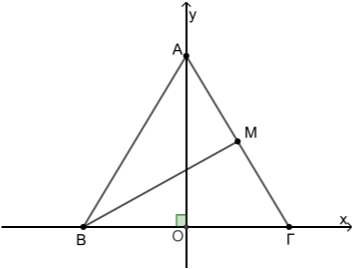
Απάντηση
α) i. Επειδή το \(A\) είναι σημείο του θετικού ημιάξονα \(Oy\) και \((OA)=8,\) θα είναι \(y_A=8,\) επομένως \(A(0,8).\) Το \(O\) είναι το μέσο του \(ΒΓ\) και τα \(Β\) και \(Γ\) είναι σημεία του αρνητικού και του θετικού ημιάξονα των \(x,\) αντίστοιχα. Επειδή \((BΓ)=12,\) θα είναι
$$|x_B|=|x_Γ|=\frac{(ΒΓ)}{2}=\frac{12}{2}=6,$$
επομένως \(B(-6,0)\) και \(Γ(6,0).\)
ii. Οι συντεταγμένες του μέσου \(M\) της πλευράς \(ΑΓ\) είναι
$$x_M=\frac{x_A+x_Γ}{2}=\frac{0+6}{2}=3$$
και
$$y_M=\frac{y_A+y_Γ}{2}=\frac{8+0}{2}=4.$$
Άρα \(Μ(3,4).\)
β) Το μήκος της διαμέσου \(ΒΜ\) είναι
\begin{align}(ΒΜ)&=\sqrt{(x_M-x_B)^2+(y_M-y_B)^2}\\ &=\sqrt{(3+6)^2+(4-0)^2}\\ &=\sqrt{97}.\end{align}
Θέμα: 14666 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}=(1,-3)\) και \(\vec{β}=(-2,-1)\).
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\vec{u}=3\vec{α}-5\vec{β}\) και \(\vec{v}=5\vec{α}-9\vec{β}\).
(Μονάδες 9)
β) Αν \(\vec{w}=2\vec{u}-\vec{v}\), να γράψετε το \(\vec{w}\) ως γραμμικό συνδυασμό των \(\vec{α},\ \vec{β}\).
(Μονάδες 9)
γ) Αν τα \(\vec{β}\), \(\vec{w}\), \(\vec{u}\) είναι τα διανύσματα θέσης των σημείων \(Κ\), \(Λ\) και \(Μ\), αντιστοίχως, να αποδείξετε ότι τα σημεία αυτά είναι συνευθειακά.
(Μονάδες 7)
Απάντηση
α) Είναι
\begin{align}\vec{u}&=3\vec{α}-5\vec{β}\\ &=3(1,-3)-5(-2,-1)\\ &=(3,-9)-(-10,-5)\\ &=(13,-4)\end{align}
και
\begin{align}\vec{v}&=5\vec{α}-9\vec{β}\\ &=5(1,-3)-9(-2,-1)\\ &=(5,-15)-(-18,-9)\\ &=(23,-6).\end{align}
β) Έχουμε
\begin{align}\vec{w}&=2\vec{u}-\vec{v}\\ &=2(3\vec{α}-5\vec{β})-(5\vec{α}-9\vec{β})\\ &=6\vec{α}-10\vec{β}-5\vec{α}+9\vec{β}\\ &=\vec{α}-\vec{β}.\end{align}
γ) Είναι
\begin{align}\overrightarrow{ΚΛ}&=\vec{w}-\vec{β}\\ &=\vec{α}-\vec{β}-\vec{β}\\ &=\vec{α}-2\vec{β}\end{align}
και
\begin{align}\overrightarrow{ΛΜ}&=\vec{u}-\vec{w}\\ &=3\vec{α}-5\vec{β}-\vec{α}+\vec{β}\\ &=2\vec{α}-4\vec{β}\\ &=2(\vec{α}-2\vec{β})\\ &=2\cdot\overrightarrow{ΚΛ}.\end{align}
Άρα τα διανύσματα \(\overrightarrow{ΚΛ}\) και \(\overrightarrow{ΛΜ}\) είναι παράλληλα, οπότε τα σημεία \(Κ\), \(Λ\), \(Μ\) είναι συνευθειακά.
Θέμα: 15002 (ΘΕΜΑ 2ο)
Δίνονται τα σημεία \(Α(0,5)\) και \(Δ(4,5)\) και τα διανύσματα \(\overrightarrow{ΑΒ}=(3,-3)\) και \(\overrightarrow{AΓ}=(3,1)\).
α)Να αποδείξετε ότι το σημείο \(Γ\) έχει συντεταγμένες \(Γ(3,6)\).
(Μονάδες 11)
β) Να βρείτε τις συντεταγμένες του διανύσματος \(\overrightarrow{ΓΔ}\).
(Μονάδες 6)
Να αποδείξετε ότι \(\overrightarrow{AΒ}//\overrightarrow{ΓΔ}\).
(Μονάδες 8)
Απάντηση
α) Αν \(Γ(x_{Γ},y_{Γ})\) τότε:
$$\overrightarrow{ΑΓ}=(3,1)$$ $$\Leftrightarrow (x_{Γ}-0,y_{Γ}-5)=(3,1)$$ $$\Leftrightarrow x_{Γ}=3 \text{ και } y_{Γ}-5=1$$ $$\Leftrightarrow y_{Γ}=6$$
Άρα, \(Γ(3,6)\).
β)
i.Είναι
$$\overrightarrow{ΓΔ}=(4-3,5-6)$$ $$\Leftrightarrow \overrightarrow{ΓΔ}=(1,-1)$$
ii.Έχουμε ότι:
$$\begin{align}\det{(\overrightarrow{AB},\overrightarrow{ΓΔ})}&=|\array{3\ \ -3 \cr 1\ \ -1}|\\ &=3(-1)-(-3)⋅1\\ &=-3+3=0 \end{align}$$
(Εναλλακτικά: \(\overrightarrow{AB}=(3,-3)=3(1,-1)=3\overrightarrow{ΓΔ}\).)
Άρα, τα διανύσματα \(\overrightarrow{ΑΒ}\) και \(\overrightarrow{ΓΔ}\) είναι παράλληλα.
Θέμα: 16151 (ΘΕΜΑ 2ο)
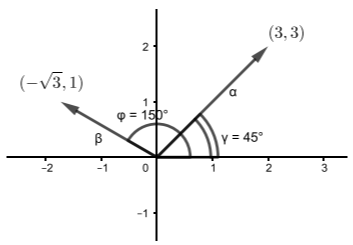
Δίνονται τα διανύσματα \(\vec{α}=(3,3)\) και \(\vec{β}=(-\sqrt{3},1)\).
α) Να βρείτε το συντελεστή διεύθυνσης των διανυσμάτων \(\vec{α}\) και \(\vec{β}\) καθώς και τη γωνία που σχηματίζει το καθένα από αυτά με τον άξονα \(x'x\).
(Μονάδες 16)
β) Να βρείτε τη γωνία \((\widehat{\vec{α},\vec{β}})\).
(Μονάδες 9)
Απάντηση
α) Είναι \(λ_\vec{α}=\dfrac{3}{3}=1\) και \(λ_\vec{β}=\dfrac{1}{-\sqrt{3}}=-\dfrac{\sqrt{3}}{3}\). Αν \(ω\) είναι η γωνία που σχηματίζει το διάνυσμα \(\vec{α}\) με τον άξονα \(x'x\) και \(φ\) η γωνία που σχηματίζει το διάνυσμα \(\vec{β}\) με τον άξονα \(x'x\), τότε \(εφω=λ_\vec{α}=1\) και \(εφφ=λ_\vec{β}=-\dfrac{\sqrt{3}}{3}\).
Το διάνυσμα \(\vec{α}\) βρίσκεται στο \(1^ο\) τεταρτημόριο, άρα \(ω=45^ο\) και το διάνυσμα \(\vec{β}\) βρίσκεται στο \(2^ο\) τεταρτημόριο, άρα \(φ=150^ο\).
β) Η γωνία \((\widehat{\vec{α},\vec{β}})\) ισούται με τη γωνία που σχηματίζει το διάνυσμα \(\vec{β}\) με τον άξονα \(x'x\) αν αφαιρέσουμε τη γωνία που σχηματίζει το διάνυσμα \(\vec{α}\) με τον \(x'x\).
Δηλαδή \((\widehat{\vec{α},\vec{β}})=150^o-45^o=105^o\).
Θέμα: 16579 (ΘΕΜΑ 2ο)
Δίνονται τα σημεία \(Α(2,1)\) και \(Β(6,7)\) του καρτεσιανού επιπέδου \(Οxy.\)
α) Να σχεδιάσετε το διάνυσμα \(\vec{AB}.\)
(Μονάδες 7)
β) Αν \(\vec{v}=\vec{AB}\) να βρείτε τις συντεταγμένες του διανύσματος \(\vec{v}.\)
(Μονάδες 8)
γ) Να αποδείξετε ότι τα διανύσματα \(\vec{u}=(−8,−12)\) και \(\vec{v}\) του β) ερωτήματος είναι αντίρροπα.
(Μονάδες 10)
Απάντηση
α) Σχεδιάζουμε τους άξονες του καρτεσιανού επιπέδου και τα δύο σημεία \(𝛢(2,1)\) και \(𝛣(6,7).\) Στη συνέχεια σχεδιάζουμε το διάνυσμα \(\vec{AB}\) με αρχή το \(Α\) και πέρας το \(Β.\)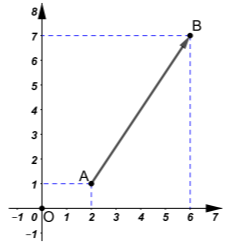
β)
$$\begin{align} \vec{v}=\vec{AB} & =(𝑥_𝛣−𝑥_𝛢, 𝑦_𝛣−𝑦_𝐴) \\ & =(6−2,\ 7−1)\\ &=(4,\ 6).\end{align}$$
γ) Παρατηρούμε ότι:
$$\begin{align} \vec{u} & =(−8,−12)\\ & =(−2\cdot 4,\ −2\cdot 6) \\ &=−2\cdot (4,\ 6)\\ &=−2\cdot \vec{v}.\end{align}$$
Εφόσον υπάρχει αρνητικός πραγματικός αριθμός \(𝜆=−2\), ώστε \(\vec{u}=𝜆\cdot \vec{v}\), τα διανύσματα \(\vec{u}\) και \(\vec{v}\) είναι αντίρροπα.
Θέμα: 16580 (ΘΕΜΑ 2ο)
Σε καρτεσιανό επίπεδο \(Οxy\) δίνονται τα σημεία \(Α(2,4), Β(11,5), Γ(3,7)\) και ένα σημείο \(Δ\) ώστε το \(\overrightarrow{ΑΔ}\) να είναι ίσο με το άθροισμα των \(\overrightarrow{ΑΒ}\) και \(\overrightarrow{ΑΓ}\). Να υπολογίσετε τις συντεταγμένες:
α) των διανυσμάτων \(\overrightarrow{ΑΒ}\) και \(\overrightarrow{ΑΓ}\).
(Μονάδες 12)
β) του διανύσματος \(\overrightarrow{ΑΔ}\).
(Μονάδες 8)
γ) του σημείου \(Δ\).
(Μονάδες 5)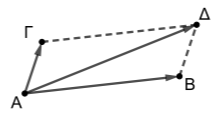
Απάντηση
α) Για τις συντεταγμένες του \(\overrightarrow{ΑB}\) είναι:
$$\overrightarrow{ΑΒ}=(x_Β-x_Α,y_Β-y_Α)=(11-2,5-4)=(9,1).$$
Όμοια:
$$\overrightarrow{ΑΓ}=(x_Γ-x_A, y_Γ-y_A)=(3-2,7-4)=(1,3).$$
β) Το διάνυσμα \(\overrightarrow{ΑΔ}\) είναι ίσο με το διάνυσμα \(\overrightarrow{ΑΒ}+\overrightarrow{ΑΓ}\). Άρα
$$\overrightarrow{ΑΔ}=\overrightarrow{ΑΒ}+\overrightarrow{ΑΓ}=(9+1,1+3)=(10,4).$$
γ) Έχουμε \(\overrightarrow{ΑΔ}=(x_Δ-x_Α ,y_Δ−y_Α)\). Αντικαθιστώντας τις συντεταγμένες του σημείου \(Α\) και τις συντεταγμένες του διανύσματος \(\overrightarrow{ΑΔ}\), η τελευταία ισότητα γίνεται:
\begin{align}&(10,4)=(x_Δ-2, y_Δ-4)\\ \iff&\begin{cases}x_Δ-2=10\\y_Δ-4=4\end{cases}\\ \iff&\begin{cases}x_Δ=12\\y_Δ=8\end{cases}.\end{align}
Άρα \(Δ(12,8)\).
Θέμα: 16581 (ΘΕΜΑ 2ο)
Σε καρτεσιανό επίπεδο \(Οxy\) δίνονται τα σημεία \(𝛢(−1,6),\ 𝛣(1,2)\) και \(𝛤(3,−2).\)
α) Να υπολογίσετε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{BΓ}.\)
(Μονάδες 12)
β) Να αποδείξετε ότι τα σημεία \(Α,\ Β\) και \(Γ\) είναι συνευθειακά.
(Μονάδες 6)
γ) Να αποδείξετε ότι το \(Β\) είναι μέσο του ευθύγραμμου τμήματος \(ΑΓ.\)
(Μονάδες 7)
Απάντηση
α) Είναι:
$$\begin{align} \overrightarrow{AB} & =(𝑥_𝛣−𝑥_𝐴,\ 𝑦_𝐵−𝑦_𝐴) \\ &=(1−(−1),\ 2−6)\\ & =(2,−4).\end{align}$$
Επίσης:
$$\begin{align} \overrightarrow{ΒΓ} & =(𝑥_𝛤−𝑥_𝛣,\ 𝑦_𝛤−𝑦_𝛣)\\ &=(3−1,\ −2−2)\\ &=(2,−4).\end{align}$$
β) Από την απάντηση στο ερώτημα α) παρατηρούμε ότι \(\overrightarrow{AB} =\overrightarrow{BΓ}.\)
Επομένως τα διανύσματα είναι συγγραμμικά και εφόσον το \(Β\) είναι κοινό σημείο συμπεραίνουμε ότι τα σημεία \(Α,\ Β\) και \(Γ\) είναι συνευθειακά.
γ) Εφόσον \(\overrightarrow{AB} =\overrightarrow{BΓ}\) συμπεραίνουμε ότι το \(Β\) είναι μέσο του ευθύγραμμου τμήματος \(ΑΓ.\)
Θέμα: 14586 (ΘΕΜΑ 2ο)
Δίνονται τα σημεία \(Α(1,2)\), \(Β(3,4)\) και \(Γ(5,-2)\).
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\), \(\overrightarrow{ΑΓ}\) και να αποδείξετε ότι η γωνία \(\hat{A}\) είναι ορθή.
(Μονάδες 9)
β) Αν \(Μ\) είναι το μέσο του \(ΒΓ\), να βρείτε τα μέτρα των \(\overrightarrow{AM}\) και \(\overrightarrow{ΒΓ}\).
(Μονάδες 8)
γ) Να γραφτεί το \(\overrightarrow{ΒΓ}\) ως γραμμικός συνδυασμός των \(\overrightarrow{ΑΓ}\) και \(\overrightarrow{AM}\).
(Μονάδες 8)
Απάντηση
α) Είναι
$$\overrightarrow{AB}=(3-1,4-2)=(2,2)$$
και
$$\overrightarrow{AΓ}=(5-1,-2-2)=(4,-4).$$
Οπότε
$$\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}=2\cdot4+2\cdot(-4)=0$$
που σημαίνει ότι \(\overrightarrow{AB}\perp\overrightarrow{ΑΓ}\), οπότε \(\hat{A}=90^0\).
β) Το \(Μ\) είναι το μέσο του \(ΒΓ\), άρα οι συντεταγμένες του είναι \(\left(\dfrac{3+5}{2},\dfrac{-2+4}{2}\right)\), δηλαδή \(Μ(4,1)\) και \(\overrightarrow{AM}=(3,-1)\), άρα
$$|\overrightarrow{AM}|=\sqrt{3^2+(-1)^2}=\sqrt{10}.$$
To τρίγωνο \(ΑΒΓ\) είναι ορθογώνιο στο \(Α\) και η \(ΑΜ\) είναι διάμεσος, άρα \((ΒΓ)=2(ΑΜ)\) και επομένως
$$|\overrightarrow{ΒΓ}|=2|\overrightarrow{AM}|=2\sqrt{10}.$$
γ) Είναι
\begin{align}\overrightarrow{ΒΓ}&=2\overrightarrow{ΜΓ}\\ &=2(\overrightarrow{MA}+\overrightarrow{AΓ})\\ &=-2\overrightarrow{AM}+2\overrightarrow{ΑΓ}.\end{align}
Θέμα: 15010 (ΘΕΜΑ 2ο)
Δίνονται τα μη συνευθειακά σημεία του επιπέδου \(Α\), \(Β\), \(Γ\) και τα διανύσματα \(\overrightarrow{ΒΔ}\) και \(\overrightarrow{ΓΕ}\) τέτοια ώστε \(\overrightarrow{ΒΔ}=\overrightarrow{ΒΑ}+\overrightarrow{BΓ}\) και \(\overrightarrow{ΓΕ}=\overrightarrow{ΓΑ}+\overrightarrow{ΓΒ}\).
α) i. Να δείξετε ότι \(\overrightarrow{ΑΔ}=\overrightarrow{ΒΓ}\) και \(\overrightarrow{AE}=\overrightarrow{ΓΒ}\).
(Μονάδες 8)
ii. Να δείξετε ότι τα διανύσματα \(\overrightarrow{ΑΔ}\) και \(\overrightarrow{AE}\) είναι αντίθετα.
(Μονάδες 8)
β) Να δικαιολογήσετε γιατί τα σημεία \(A\), \(Δ\) και \(Ε\) είναι συνευθειακά.
(Μονάδες 9)
Απάντηση
α) i. Είναι
$$\overrightarrow{ΑΔ}=\overrightarrow{AB}+\overrightarrow{ΒΔ}=\overrightarrow{AB}+(\overrightarrow{BA}+\overrightarrow{ΒΓ})=\overrightarrow{ΒΓ}\quad(1)$$
και
$$\overrightarrow{AE}=\overrightarrow{ΑΓ}+\overrightarrow{ΓΕ}=\overrightarrow{ΑΓ}+(\overrightarrow{ΓΑ}+\overrightarrow{ΓΒ})=\overrightarrow{ΓΒ}\quad(2)$$
ii. Από τις σχέσεις \((1)\) και \((2)\) συμπεραίνουμε ότι \(\overrightarrow{ΑΔ}=-\overrightarrow{ΑΕ}\), δήλαδη τα διανύσματα \(\overrightarrow{ΑΔ}\) και \(\overrightarrow{ΑΕ}\) είναι αντίθετα.
β) Από το (α) ερώτημα είναι \(\overrightarrow{ΑΔ}=(-1)\overrightarrow{ΑΕ}\), οπότε τα διανύσματα \(\overrightarrow{ΑΔ}\) και \(\overrightarrow{AE}\) είναι παράλληλα. Επιπλέον έχουν κοινό σημείο το \(Α\), άρα τα \(Α\), \(Δ\) και \(Ε\) είναι συνευθειακά.
Θέμα: 22554 (ΘΕΜΑ 2ο)
Στο καρτεσιανό επίπεδο \(Oxy\), με μοναδιαία διανύσματα των αξόνων \(x'x\), \(y'y\) τα \(\vec{i}\), \(\vec{j}\), αντίστοιχα, τα σημεία \(Α\) και \(Β\) έχουν διανύσματα θέσεως \(\overrightarrow{OA}=3\vec{i}+2\vec{j}\) και \(\overrightarrow{OB}=6\vec{i}-\vec{j}.\) Έστω \(Μ\) ένα σημείο τέτοιο ώστε \(\overrightarrow{OM}=\frac{1}{5}(2\overrightarrow{OA}-\overrightarrow{OB}).\)
α) Να δείξετε ότι:
i. \(\overrightarrow{AB}=3\vec{i}-3\vec{j}.\)
(Μονάδες 8)
ii. \(\overrightarrow{OM}=\vec{j}.\)
(Μονάδες 8)
β) Να βρείτε το εσωτερικό γινόμενο \(\overrightarrow{AB}\cdot\overrightarrow{OM}.\)
(Μονάδες 9)
Απάντηση
α) Είναι:
i.
\begin{align}\overrightarrow{AB}&=\overrightarrow{OB}-\overrightarrow{OA}\\ &=6\vec{i}-\vec{j}-(3\vec{i}+2\vec{j})\\ &=6\vec{i}-\vec{j}-3\vec{i}-2\vec{j}\\ &=3\vec{i}-3\vec{j}.\end{align}
ii.
\begin{align}\overrightarrow{OM}&=\frac{1}{5}(2\overrightarrow{OA}-\overrightarrow{OB})\\ &=\frac{1}{5}(2(3\vec{i}+2\vec{j})-(6\vec{i}-\vec{j}))\\ &=\frac{1}{5}(6\vec{i}+4\vec{j}-6\vec{i}+\vec{j})\\ &=\frac{1}{5}5\vec{j}\\ &=\vec{j}.\end{align}
β) Για τα μοναδιαία διανύσματα \(\vec{i}\) και \(\vec{j}\) ισχύουν \(\vec{i}\cdot\vec{j}=0\) και \(\vec{j}^2=1\). Επομένως,
\begin{align}\overrightarrow{AB}\cdot\overrightarrow{OM}&=(3\vec{i}-3\vec{j})\cdot\vec{j}\\ &=3\vec{i}\cdot\vec{j}-3\vec{j}^2\\ &=3\cdot 0-3\cdot 1\\ &=-3.\end{align}
Θέμα: 22170 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}=(-1,3)\), \(\vec{β}=(-2,-\dfrac{1}{2})\) και \(\vec{v}=(x^2,x-1)\).
α) Να βρείτε τις συντεταγμένες του διανύσματος \(\vec{u}=\vec{α}-2\vec{β}\).
(Μονάδες 7)
β) Να βρείτε τους αριθμούς \(x\) για τους οποίους τα διανύσματα \(\vec{u}=(3,4)\) και \(\vec{v}\) είναι κάθετα.
(Μονάδες 9)
γ) Να βρείτε τους αριθμούς \(x\) για τους οποίους τα διανύσματα \(\vec{v}\) και \(\vec{β}\) είναι συγγραμμικά.
(Μονάδες 9)
Απάντηση
α) Είναι
\begin{align}\vec{u}&=\vec{α}-2\vec{β}\\ &=(-1,3)-2(-2,-\frac{1}{2})\\ &=(-1,3)+(4,1)\\ &=(-1+4,3+1)\\ &=(3,4).\end{align}
β) Για να είναι κάθετα τα διανύσματα θα πρέπει το εσωτερικό τους γινόμενο να είναι ίσο με μηδέν, δηλαδή
\begin{align}&\vec{u}\cdot\vec{v}=0\\ \iff&(3,4)\cdot(x^2,x-1)=0\\ \iff&3x^2+4(x-1)=0\\ \iff&3x^2+4x-4=0.\end{align}
Η διακρίνουσα είναι \(64\) και οι ρίζες \(x=\dfrac{2}{3}\) και \(x=-2\).
γ) Για να είναι τα διανύσματα \(\vec{v}\) και \(\vec{β}\) συγγραμμικά πρέπει η ορίζουσα των συντελεστών τους να είναι μηδέν. Είναι
\begin{align}&\begin{vmatrix}x^2&x-1\\-2&-\frac{1}{2}\end{vmatrix}=0\\ \iff&-\frac{1}{2}x^2-(-2)(x-1)=0\\ \iff&-\frac{1}{2}x^2+2x-2\\ \iff&x^2-4x+4=0\\ \iff&x=2.\end{align}
Θέμα: 21885 (ΘΕΜΑ 4ο)
Δίνεται τρίγωνο \(ΑΒΓ\) και \(Δ,Ε\) σημεία εσωτερικά των πλευρών \(ΑΒ\) και \(ΑΓ\), αντίστοιχα, τέτοια ώστε \(\overrightarrow{AB}=κ\cdot\overrightarrow{ΑΔ}\) και \(\overrightarrow{ΑΓ}=λ\cdot\overrightarrow{AE}\), όπου \(κ\) και \(λ\) θετικοί πραγματικοί αριθμοί. Αν \(\overrightarrow{AB}=\vec{α}\) και \(\overrightarrow{ΑΓ}=\vec{β}\), τότε:
α) Να εκφράσετε τα διανύσματα \(\overrightarrow{ΔΕ}\) και \(\overrightarrow{ΒΓ}\) ως γραμμικό συνδυασμό των \(\vec{α}\) και \(\vec{β}\).
(Μονάδες 8)
β) i. Αν \(κ=λ\), να αποδείξετε ότι \(\overrightarrow{ΒΓ}\parallel \overrightarrow{ΔΕ}\) και \(|\overrightarrow{ΒΓ}|=κ\cdot|\overrightarrow{ΔΕ}|\).
(Μονάδες 10)
ii. Aν \(κ=λ=2\), να γράψετε τη σχέση που συνδέει τα διανύσματα \(\overrightarrow{ΔΕ}\) και \(\overrightarrow{ΒΓ}\) και να διατυπώσετε λεκτικά ποιο γνωστό θεώρημα της Ευκλείδειας Γεωμετρίας έχει αποδειχθεί.
(Μονάδες 7)
Απάντηση
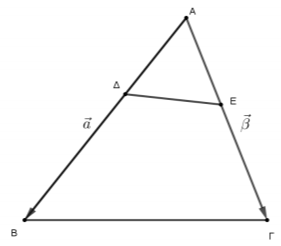
α) Είναι
\begin{align}\overrightarrow{ΔΕ}&=\overrightarrow{ΔΑ}+\overrightarrow{AE}\\ &=-\frac{1}{κ}\cdot\vec{α}+\frac{1}{λ}\cdot\vec{β}\end{align}
και
\begin{align}\overrightarrow{ΒΓ}&=\overrightarrow{BA}+\overrightarrow{ΑΓ}\\ &=-\vec{α}+\vec{β}.\end{align}
β) i. Αν \(κ=λ\) τότε
\begin{align}\overrightarrow{ΒΓ}&=-\vec{α}+\vec{β}\\ &=κ(-\frac{1}{κ}\vec{α}+\frac{1}{κ}\vec{β})\\ &=κ\cdot\overrightarrow{ΔΕ}\end{align}
άρα \(\overrightarrow{ΒΓ}//\overrightarrow{ΔΕ}\) και \(|\overrightarrow{ΒΓ}|=κ\cdot|\overrightarrow{ΔΕ}|\).
ii.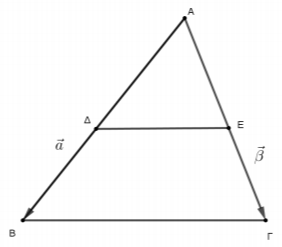
Αν \(κ=λ=2\), τότε τα σημεία \(Δ\) και \(Ε\) είναι τα μέσα των \(ΑΒ\) και \(ΑΓ\), αντίστοιχα, και δείξαμε ότι \(\overrightarrow{ΒΓ}\parallel \overrightarrow{ΔΕ}\) και \(|\overrightarrow{ΒΓ}|=2\cdot|\overrightarrow{ΔΕ}|\), επομένως \(ΔΕ\parallel ΒΓ\) και \(ΒΓ=2\cdot ΔΕ\). Αποδείξαμε δηλαδή ότι το ευθύγραμμο τμήμα που ενώνει τα μέσα δύο πλευρών τριγώνου είναι παράλληλο με την τρίτη πλευρά του τριγώνου και ισούται με το μισό της τρίτης πλευράς.
Θέμα: 21165 (ΘΕΜΑ 2ο)
Θεωρούμε το παραλληλόγραμμο \(ΑΒΓΔ\) και έστω \(\overrightarrow{ΑΒ}=\vec{α}\) και \(\overrightarrow{ΑΔ}=\vec{β}\). Τα σημεία \(Ε\) και \(Ζ\) είναι τέτοια ώστε \(\overrightarrow{AE}=-\dfrac{1}{2}\cdot\overrightarrow{AB}\) και \(\overrightarrow{AZ}=\dfrac{1}{3}\cdot\overrightarrow{ΑΔ}\).
α) Να αποδείξετε ότι \(\overrightarrow{EZ}=\dfrac{1}{2}\cdot\vec{α}+\dfrac{1}{3}\vec{β}\) και \(\overrightarrow{ZΓ}=\vec{α}+\dfrac{2}{3}\cdot\vec{β}\).
(Μονάδες 10)
β) Να αποδείξετε ότι \(\overrightarrow{ZΓ}=2\overrightarrow{EZ}\).
(Μονάδες 9)
γ) Να δείξετε ότι τα σημεία \(Ζ\), \(Ε\) και \(Γ\) είναι συνευθειακά.
(Μονάδες 6)

Απάντηση
α) Αφού είναι \(\overrightarrow{ΑΒ}=\vec{α}\) και \(\overrightarrow{ΑΔ}=\vec{β}\), έχουμε ότι τα διανύσματα \(\overrightarrow{ΑΕ}\) και \(\overrightarrow{ΑΖ}\) γράφονται
$$\overrightarrow{AE}=-\frac{1}{2}\cdot\overrightarrow{AB}=-\frac{1}{2}\cdot\vec{α}$$
και
$$\overrightarrow{AZ}=\frac{1}{3}\cdot\overrightarrow{ΑΔ}=\frac{1}{3}\cdot\vec{β}.$$
Tότε για τα διανύσματα \(\overrightarrow{ΕΖ}\) και \(\overrightarrow{ΖΓ}\) έχουμε ότι
\begin{align}\overrightarrow{EZ}&=\overrightarrow{AZ}-\overrightarrow{AE}\\ &=\frac{1}{3}\cdot\vec{β}-(-\frac{1}{2}\cdot\vec{α})\\ &=\frac{1}{2}\cdot\vec{α}+\frac{1}{3}\cdot\vec{β}\end{align}
και
\begin{align}\overrightarrow{ΖΓ}&=\overrightarrow{AΓ}-\overrightarrow{AZ}\\ &=\overrightarrow{AB}+\overrightarrow{ΑΔ}-\overrightarrow{AZ}\\ &=\vec{α}+\vec{β}-\frac{1}{3}\cdot\vec{β}\\ &=\vec{α}+\frac{2}{3}\cdot\vec{β}.\end{align}
β) Επειδή \(\overrightarrow{ΕΖ}=\frac{1}{2}\cdot\vec{α}+\frac{1}{3}\cdot\vec{β}\) και \(\overrightarrow{ΖΓ}=\vec{α}+\frac{2}{3}\vec{β}\), έχουμε ότι
$$\overrightarrow{ΖΓ}=\vec{α}+\frac{2}{3}\cdot\vec{β}=2\left(\frac{1}{2}\vec{α}+\frac{1}{3}\vec{β}\right)=2\overrightarrow{EZ}.$$
γ) Επειδή είναι \(\overrightarrow{ΖΓ}//\overrightarrow{ΕΖ}\) και τα διανύσματα έχουν κοινό άκρο το σημείο \(Ζ\), έχουμε το συμπέρασμα ότι τα σημεία \(Ζ\), \(Ε\) και \(Γ\) είναι συνευθειακά.
Θέμα: 20888 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}\), \(\vec{β}\) και \(\vec{γ}\), για τα οποία ισχύουν \(|\vec{α}|=4\), \(|\vec{β}|=5\), \((\widehat{\vec{α},\vec{β}})=\dfrac{2π}{3}\) και \(\vec{γ}=2\vec{α}+3\vec{β}\). Να υπολογίσετε:
α) Το εσωτερικό γινόμενο \(\vec{α}\cdot\vec{β}\).
(Μονάδες 10)
β) το μέτρο του διανύσματος \(\vec{γ}\).
(Μονάδες 15)
Απάντηση
α) Έχουμε
\begin{align}\vec{α}\cdot\vec{β}&=|\vec{α}|\cdot|\vec{β}|\cdot συν(\widehat{\vec{α},\vec{β}})\\ &=4\cdot 5\cdot συν\frac{2π}{3}\\ &=20\cdot\left(-\frac{1}{2}\right)\\ &=-10.\end{align}
β) Έχουμε
\begin{align}&\vec{γ}=2\vec{α}+3\vec{β}\\ \implies&\vec{γ}^2=(2\vec{α}+3\vec{β})^2\\ \implies&|\vec{γ}|^2=4\vec{α}^2+12\vec{α}\cdot\vec{β}+9\vec{β}^2\\ \implies&|\vec{γ}|^2=4|\vec{α}|^2+12\vec{α}\cdot\vec{β}+9|\vec{β}|^2\\ \implies&|\vec{γ}|^2=4\cdot 4^2+12\cdot(-10)+9\cdot 5^2\\ \implies&|\vec{γ}|^2=64-120+225\\ \implies&|\vec{γ}|^2=169\\ \implies&|\vec{γ}|=13.\end{align}
Θέμα: 20685 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{u}=(1,1)\), \(\vec{w}=(-10,2)\) και τα σημεία \(Α(-1,2)\), \(Β(β,0)\), \(Γ(0,γ)\). Τα διανύσματα \(\vec{u}\), \(\overrightarrow{ΑΒ}\) είναι κάθετα και το διάνυσμα \(\vec{w}\) είναι παράλληλο στο διάνυσμα \(\overrightarrow{ΑΓ}\).
α) Να βρείτε τις συντεταγμένες του διανύσματος \(\overrightarrow{AB}\) και να αποδείξετε ότι \(β=1\).
(Μονάδες 9)
β) Να βρείτε τις συντεταγμένες του διανύσματος \(\overrightarrow{ΑΓ}\) και να αποδείξετε ότι \(γ=\dfrac{9}{5}\).
(Μονάδες 9)
γ) Να υπολογίσετε το εσωτερικό γινόμενο \(\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}\).
(Μονάδες 7)
Απάντηση
α) Οι συντεταγμένες του διανύσματος \(\overrightarrow{AB}\) είναι
$$\overrightarrow{AB}=(β-(-1),0-2)=(β+1,-2).$$
Αφού τα διανύσματα \(\vec{u}\), \(\overrightarrow{AB}\) είναι κάθετα, θα ισχύει \(\vec{u}\cdot\overrightarrow{AB}=0\). Άρα
\begin{align}&1\cdot(β+1)+1\cdot(-2)=0\\ \iff&β+1-2=0\\ \iff&β=1.\end{align}
β) Οι συντεταγμένες του διανύσματος \(\overrightarrow{AΓ}\) είναι
$$\overrightarrow{AΓ}=(0-(-1),γ-2)=(1,γ-2).$$
Αφού τα διανύσματα \(\vec{w}\), \(\overrightarrow{ΑΓ}\) είναι παράλληλα, η ορίζουσα τους θα ισούται με μηδέν, δηλαδή
\begin{align}&\begin{vmatrix}-10&2\\1&γ-2\end{vmatrix}=0\\ \iff&-10(γ-2)-2\cdot 1=0\\ \iff&γ=\frac{9}{5}.\end{align}
γ) Από τα ερωτήματα (α), (β) έχουμε ότι \(\overrightarrow{AB}=(2,-2)\) και \(\overrightarrow{ΑΓ}=\left(1,-\dfrac{1}{5}\right)\). Tο εσωτερικό γινόμενο των διανυσμάτων \(\overrightarrow{AB}\), \(\overrightarrow{ΑΓ}\) είναι
\begin{align}\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}&=2\cdot 1+(-2)\cdot\left(-\frac{1}{5}\right)\\ &=2+\frac{2}{5}\\ &=\frac{12}{5}.\end{align}
Θέμα: 19038 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}=(2,3)\), \(\vec{β}=(-1,1)\) και \(\vec{γ}=(-5,-5)\).
α) Να υπολογίσετε τη γωνία που σχηματίζει το διάνυσμα \(\vec{β}\) με τον άξονα \(x'x\).
(Μονάδες 9)
β) Να αποδείξετε ότι \(|\vec{γ}|=5|\vec{β}|\).
(Μονάδες 8)
γ) Να υπολογίσετε τους πραγματικούς αριθμούς \(λ\), \(μ\) ώστε το διάνυσμα \(\vec{γ}\) να γραφεί στη μορφή \(\vec{γ}=λ\vec{α}+μ\vec{β}\).
(Μονάδες 8)
Απάντηση
α) Για τη γωνία \(ω\) που σχηματίζει το διάνυσμα \(\vec{β}\) με τον άξονα \(x'x\) είναι
$$εφω=\frac{y_{\vec{β}}}{x_{\vec{β}}}=\frac{1}{-1}=-1.$$
Αφού είναι \(x_\vec{β} < 0\) και \(y_\vec{β} > 0\), για τη γωνία \(ω\) θα ισχύει \(\dfrac{π}{2} < ω < π\). Άρα,
$$ω=π-\frac{π}{4}=\frac{3π}{4}.$$
β) Είναι
$$|\vec{γ}|=\sqrt{x_\vec{γ}^2+y_\vec{γ}^2}=\sqrt{50}=5\sqrt{2}$$
και
$$|\vec{β}|=\sqrt{x_\vec{β}^2+y_\vec{β}^2}=\sqrt{2}.$$
Επομένως, \(|\vec{γ}|=5|\vec{β}|\).
γ) Ζητάμε τους πραγματικούς αριθμούς \(λ\), \(μ\) για τους οποίους ισχύει η ισότητα
$$\vec{γ}=λ\vec{α}+μ\vec{β}.$$
Έχουμε
\begin{align}&(-5,-5)=λ(2,3)+μ(-1,1)\\ \iff&(-5,-5)=(2λ-μ,3λ+μ).\end{align}
Επομένως, είναι
$$2λ-μ=-5\quad(1)$$
και
$$3λ+μ=-5.\quad(2)$$
Με πρόσθεση κατά μέλη προκύπτει ότι
$$5λ=-10\iff λ=-2.$$
Αντικαθιστούμε στην \((2)\), οπότε
$$3\cdot(-2)+μ=-5\iff μ=-5+6=1.$$
Άρα, το διάνυσμα \(\vec{γ}\) γράφεται ως εξής:
$$\vec{γ}=-2\vec{α}+\vec{β}.$$
Θέμα: 18547 (ΘΕΜΑ 4ο)
Δίνονται τα σημεία \(Α(0,-1)\), \(Β(λ,1)\) και \(Γ(λ-2,λ-3)\), όπου \(λ\in\mathbb{R}\).
α) Να βρείτε τις τιμές του \(λ\in\mathbb{R}\) ώστε:
i. Tα σημεία \(Α\), \(Β\) και \(Γ\) να είναι κορυφές τριγώνου.
(Μονάδες 8)
ii. Το τρίγωνο \(ΑΒΓ\) να είναι ορθογώνιο με \(\hat{A}=90^ο\).
(Μονάδες 7)
β) Για \(λ=-2\), να βρείτε:
i. Το εσωτερικό γινόμενο \(\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}\).
(Μονάδες 4)
ii. Το εμβαδό του τριγώνου \(ΑΒΓ\).
(Μονάδες 6)
Απάντηση
α) i. Για να σχηματίζουν τα σημεία \(Α\), \(Β\) και \(Γ\) τρίγωνο θα πρέπει να μην βρίσκονται στην ίδια ευθεία ή αλλιώς τα διανύσματα \(\overrightarrow{AB}\), \(\overrightarrow{AΓ}\) να μην είναι παράλληλα. Είναι
$$\overrightarrow{AB}=(λ, 1+1)=(λ, 2)$$
και
$$\overrightarrow{ΑΓ}=(λ-2, λ-3+1)=(λ-2, λ-2).$$
Γνωρίζουμε ότι
\begin{align}&\overrightarrow{AB}//\overrightarrow{AΓ}\\ \iff&\det(\overrightarrow{AB},\overrightarrow{ΑΓ})=0\\ \iff&\begin{vmatrix}λ&2\\λ-2&λ-2\end{vmatrix}=0\\ \iff&λ(λ-2)-2(λ-2)=0\\ \iff&(λ-2)^2=0\\ \iff&λ=2.\end{align}
Δηλαδή τα διανύσματα \(\overrightarrow{AB}\), \(\overrightarrow{AΓ}\) είναι παράλληλα αν και μόνο αν \(λ=2\). Οπότε τα σημεία \(Α\), \(Β\) και \(Γ\) σχηματίζουν τρίγωνο για κάθε τιμή του \(λ\) που είναι διαφορετική από το \(2\).
ii. Αν το τρίγωνο \(ΑΒΓ\) είναι ορθογώνιο με \(\hat{A}=90^ο\), το εσωτερικό γινόμενο \(\overrightarrow{AB}\cdot\overrightarrow{AΓ}\) θα ισούται με μηδέν. Όμως
\begin{align}&\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}=0\\ \iff&λ(λ-2)+2(λ-2)=0\\ \iff&(λ+2)(λ-2)=0\\ \iff&λ+2=0\text{ ή }λ-2=0\\ \iff&λ=-2\text{ ή }λ=2.\end{align}
Στο ερώτημα (α.i) δείξαμε ότι για \(λ=2\) τα σημεία \(Α\), \(Β\) και \(Γ\) δεν ορίζουν τρίγωνο, οπότε το τρίγωνο \(ΑΒΓ\) είναι ορθογώνιο με \(\hat{A}=90^ο\) μόνο για την τιμή \(λ=-2\).
β) Για \(λ=-2\), έχουμε \(\overrightarrow{AB}=(-2, 2)\), \(\overrightarrow{AΓ}=(-4, -4)\) και από ερώτημα (α.ii) τα σημεία \(Α(0, -1)\), \(Β(-2, 1)\) και \(Γ(-4, -5)\) ορίζουν ορθογώνιο τρίγωνο με \(\hat{A}=90^ο\).
i. \(\overrightarrow{AB}\cdot\overrightarrow{AΓ}=0\).
ii. Είναι
\begin{align}(ABΓ)&=\frac{1}{2}|\det(\overrightarrow{AB},\overrightarrow{ΑΓ})|\\ &=\frac{1}{2}|\!\begin{vmatrix}-2&2\\-4&-4\end{vmatrix}|\\ &=\frac{1}{2}\cdot 16\\ &=8.\end{align}
Β’ τρόπος:
Είναι
$$(ΑΒΓ)=\frac{1}{2}|\overrightarrow{ΑΒ}|\cdot |\overrightarrow{AΓ}|.$$
Έχουμε
$$|\overrightarrow{AB}|=\sqrt{(-2)^2+2^2}=2\sqrt{2}$$
και
$$|\overrightarrow{ΑΓ}=\sqrt{(-4)^2+(-4)^2}=4\sqrt{2},$$
οπότε
$$(AΒΓ)=\frac{1}{2}2\sqrt{2}\cdot4\sqrt{2}=8.$$
Θέμα: 18243 (ΘΕΜΑ 3ο)
Θεωρούμε τα διανύσματα \(\vec{α}\), \(\vec{β}\) με \(|\vec{α}|=2\), \(|\vec{β}|=4\), \((\widehat{\vec{α},\vec{β}})=\dfrac{π}{3}\), και τα διανύσματα \(\vec{γ}=\vec{α}-\vec{β}\) και \(\vec{δ}=2\vec{α}+\vec{β}\).
α) Να βρείτε το \(\vec{α}\cdot\vec{β}\).
(Μονάδες 5)
β) Να βρείτε το \(\vec{γ}\cdot\vec{δ}\).
(Μονάδες 7)
γ) Να βρείτε τα \(|\vec{γ}|\), \(|\vec{δ}|\).
(Μονάδες 8)
δ) Να βρείτε τη γωνία \((\widehat{\vec{γ},\vec{δ}})\).
(Μονάδες 5)
Απάντηση
α) Είναι
\begin{align}\vec{α}\cdot\vec{β}&=|\vec{α}|\cdot|\vec{β}|\cdot συν\frac{π}{3}\\ &=2\cdot 4\cdot\frac{1}{2}\\ &=4.\end{align}
β) Είναι
\begin{align}\vec{γ}\cdot\vec{δ}&=(\vec{α}-\vec{β})\cdot(2\vec{α}+\vec{β})\\ &=2\vec{α}^2+\vec{α}\cdot\vec{β}-2\vec{α}\cdot\vec{β}-\vec{β}^2\\ &=2|\vec{α}|^2-\vec{α}\cdot\vec{β}-|\vec{β}|^2\\ &=2\cdot 2^2-4-4^2\\ &=-12.\end{align}
γ) Είναι
\begin{align}|\vec{γ}|^2&=\vec{γ}^2\\ &=(\vec{α}-\vec{β})^2\\ &=\vec{α}^2-2\vec{α}\cdot\vec{β}+\vec{β}^2\\ &=12,\end{align}
οπότε
$$|\vec{γ}|=\sqrt{12}=2\sqrt{3}.$$
Επίσης
\begin{align}|\vec{δ}|^2&=\vec{δ}^2\\ &=(2\vec{α}+\vec{β})^2\\ &=4\vec{α}^2+4\vec{α}\cdot\vec{β}+\vec{β}^2\\ &=48,\end{align}
οπότε
$$|\vec{δ}|=\sqrt{48}=4\sqrt{3}.$$
δ) Είναι
\begin{align}συν(\widehat{\vec{γ},\vec{δ}})&=\frac{\vec{γ}\cdot\vec{δ}}{|\vec{γ}|\cdot|\vec{δ}|}\\ &=\frac{-12}{2\sqrt{3}\cdot 4\sqrt{3}}\\ &=-\frac{1}{2},\end{align}
οπότε \((\widehat{\vec{γ},\vec{δ}})=\dfrac{2π}{3}\).
Θέμα: 17077 (ΘΕΜΑ 4ο)
Στο καρτεσιανό επίπεδο \(Oxy\) τα σημεία \(A\) και \(B\) έχουν διανύσματα θέσεως
$$\overrightarrow{OA}=2\vec{i}+λ\vec{j}$$
και
$$\overrightarrow{OB}=(λ+1)\vec{i}+(λ+3)\vec{j},$$
με \(λ\in\mathbb{R}\).
α) Να αποδείξετε ότι
$$\overrightarrow{AB}=(λ-1)\vec{i}+3\vec{j}.$$
(Μονάδες 6)
β) Να βρείτε την απόσταση των σημείων \(A\) και \(B\) ως συνάρτηση του \(λ\).
(Μονάδες 7)
γ) Για ποιές τιμές του \(λ\) η απόσταση των σημείων \(A\) και \(B\) είναι ίση με \(5\);
(Μονάδες 7)
δ) Θεωρήστε τον ισχυρισμό:
Υπάρχει πραγματικός αριθμός \(λ\) τέτοιος ώστε η απόσταση των σημείων \(A\) και \(B\) να παίρνει τη μικρότερη δυνατή τιμή.
Είναι αληθής ή ψευδής ο παραπάνω ισχυρισμός; Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 5)
Απάντηση
α) Είναι
\begin{align}\overrightarrow{AB}&=\overrightarrow{OB}-\overrightarrow{OA}\\ &=(λ+1)\vec{i}+(λ+3)\vec{j}-2\vec{i}-λ\vec{j}\\ &=(λ+1-2)\vec{i}+(λ+3-λ)\vec{j}\\ &=(λ-1)\vec{i}+3\vec{j}.\end{align}
β) Η απόσταση των σημείων \(A\) και \(B\) είναι ίση με
\begin{align}(AB)&=|\overrightarrow{AB}|\\ &=\sqrt{(λ-1)^2+3^2}\\ &=\sqrt{(λ-1)^2+9}\end{align}
με \(λ\in\mathbb{R}\).
γ) Είναι
\begin{align}&(AB)=5\\ \iff&\sqrt{(λ-1)^2+3^2}=5\\ \iff&(λ-1)^2+9=25\\ \iff&(λ-1)^2=16\\ \iff&(λ-1)^2=4^2\\ \iff&λ-1=\pm 4\\ \iff&λ=5\text{ ή }λ=-3.\end{align}
δ) Για κάθε πραγματικό αριθμό \(λ\) έχουμε
\begin{align}&(λ-1)^2\geq 0\\ \iff&(λ-1)^2+9\geq 9\\ \iff&\sqrt{(λ-1)^2+9}\geq\sqrt{9}\\ \iff&(AB)\geq 3,\end{align}
όπου η ισότητα ισχύει αν και μόνο αν
\begin{align}&(λ-1)^2=0\\ \iff&λ-1=0\\ \iff&λ=1.\end{align}
Άρα, για κάθε πραγματικό αριθμό \(λ\neq 1\) η απόσταση των σημείων \(A\) και \(B\) είναι \((AB) > 3\). Όταν \(λ=1\) η απόσταση των σημείων \(Α\) και \(Β\) είναι \((ΑΒ)=3\) και αυτή είναι η μικρότερη δυνατή τιμή της.
(Άλλος τρόπος: Η απόσταση των σημείων \(Α\) και \(Β\) γράφεται
\begin{align}(AB)&=\sqrt{(λ-1)^2+9}\\ &=\sqrt{λ^2-2λ+10},\ λ\in\mathbb{R}\end{align}
και παίρνει τη μικρότερη δυνατή τιμή όταν το τριώνυμο \(λ^2-2λ+10\) παρουσιάζει ελάχιστο, το οποίο συμβαίνει διότι ο συντελεστής του δευτεροβάθμιου όρου είναι \(1 > 0\). Συγκεκριμένα, συμβαίνει όταν \(λ=-\dfrac{β}{2α}\). Είναι \(α=1\), \(β=-2\) και \(γ=10\), οπότε το τριώνυμο παρουσιάζει ελάχιστο για \(λ=-\dfrac{-2}{2\cdot1}=1\).)
Επομένως ο ισχυρισμός είναι αληθής.
Θέμα: 17076 (ΘΕΜΑ 4ο)
Δίνονται τα σημεία \(Α(-3,-1)\), \(B(0,3)\) και \(M(x,y)\) του καρτεσιανού επιπέδου \(Oxy\).
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AM}\), \(\overrightarrow{MB}\) και \(\overrightarrow{AB}\).
(Μονάδες 6)
β) Να βρείτε τα μέτρα των διανυσμάτων \(\overrightarrow{AM}\), \(\overrightarrow{MB}\) και \(\overrightarrow{AB}\).
(Μονάδες 6)
γ) Να αποδείξετε ότι \(|\overrightarrow{AM}|+|\overrightarrow{MB}|\geq 5\).
(Μονάδες 6)
δ) Θεωρήστε τον ισχυρισμό:
Υπάρχει ζεύγος πραγματικών αριθμών \((x,y)\) τέτοιο ώστε να ισχύει:
$$\sqrt{(x+3)^2+(y+1)^2}+\sqrt{x^2+(y-3)^2}=4.$$
Είναι αληθής ή ψευδής ο παραπάνω ισχυρισμός; Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 7)
Απάντηση
α) Οι συντεταγμένες των διανυσμάτων \(\overrightarrow{AM}\), \(\overrightarrow{MB}\) και \(\overrightarrow{AB}\) είναι αντίστοιχα
\begin{align}&\overrightarrow{AM}=(x_M-x_A,y_M-y_A)=(x+3,y+1),\\ &\overrightarrow{MB}=(x_B-x_M,y_B-y_M)=(-x,3-y),\\ &\overrightarrow{AB}=(x_B-x_A,y_B-y_A)=(3,4).\end{align}
β) Τα μέτρα των διανυσμάτων \(\overrightarrow{AM}\), \(\overrightarrow{MB}\) και \(\overrightarrow{AB}\) είναι αντίστοιχα
\begin{align}&|\overrightarrow{AM}|=\sqrt{(x+3)^2+(y+1)^2},\\ &|\overrightarrow{MB}|=\sqrt{x^2+(y-3)^2},\\ &|\overrightarrow{AB}|=\sqrt{3^2+4^2}=\sqrt{25}=5.\end{align}
γ) Για το μέτρο του αθροίσματος δύο διανυσμάτων ισχύει
\begin{align}&|\overrightarrow{AM}+\overrightarrow{MB}|\leq |\overrightarrow{AM}|+|\overrightarrow{MB}|\\ \iff&|\overrightarrow{AB}|\leq |\overrightarrow{AM}|+|\overrightarrow{MB}|\\ \iff&5\leq |\overrightarrow{AM}|+|\overrightarrow{MB}|\\ \iff&|\overrightarrow{AM}|+|\overrightarrow{MB}|\geq 5.\end{align}
δ) Από το (γ) ερώτημα, για οποιοδήποτε σημείο \(M(x,y)\) του καρτεσιανού επιπέδου ισχύει
$$|\overrightarrow{AM}|+|\overrightarrow{MB}|\geq 5,$$
οπότε αντικαθιστώντας από το (β) ερώτημα θα έχουμε
$$\sqrt{(x+3)^2+(y+1)^2}+\sqrt{x^2+(y-3)^2}\geq 5.$$
Οπότε δεν υπάρχει ζεύγος \((x,y)\) πραγματικών αριθμών ώστε να ισχύει
$$\sqrt{(x+3)^2+(y+1)^2}+\sqrt{x^2+(y-3)^2}=4.$$
Επομένως ο ισχυρισμός είναι ψευδής.
Θέμα: 17075 (ΘΕΜΑ 2ο)
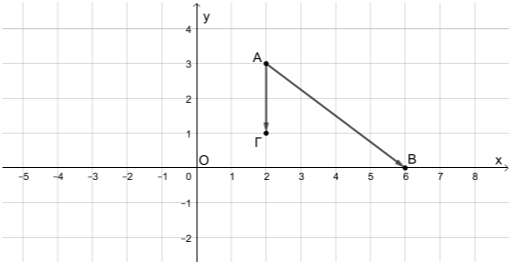
Στο παρακάτω σχήμα δίνονται τα διανύσματα \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}\) του καρτεσιανού επιπέδου \(Oxy\).
α) Να αποδείξετε ότι \(\overrightarrow{AB}=(4,-3)\) και \(\overrightarrow{ΑΓ}=(0,-2)\).
(Μονάδες 12)
β) Να υπολογίσετε το εσωτερικό γινόμενο των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}\).
(Μονάδες 13)
Απάντηση
α) Παρατηρούμε ότι τα σημεία \(A\), \(B\) και \(Γ\) έχουν συντεταγμένες \(A(2,3)\), \(B(6,0)\) και \(Γ(2,1)\). Επομένως οι συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{ΑΓ}\) θα είναι
\begin{align}\overrightarrow{AB}&=(x_B-x_A,y_B-y_A)\\ &=(6-2,0-3)\\ &=(4,-3)\end{align}
και
\begin{align}\overrightarrow{ΑΓ}&=(x_Γ-x_A,y_Γ-y_A)\\ &=(2-2,1-3)\\ &=(0,-2).\end{align}
β) Το εσωτερικό γινόμενο των διανυσμάτων \(\overrightarrow{ΑΒ}\) και \(\overrightarrow{ΑΓ}\) είναι
$$\overrightarrow{ΑB}\cdot\overrightarrow{ΑΓ}=x_1\cdot x_2+y_1\cdot y_2,$$
όπου \((x_1,y_1)\) και \((x_2,y_2)\) είναι οι συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}\), αντίστοιχα. Aντικαθιστώντας τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\) και \(\overrightarrow{AΓ}\), από το προηγούμενο ερώτημα, θα έχουμε
$$\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}=4\cdot 0+(-3)\cdot(-2)=0+6=6.$$
Θέμα: 16428 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}\) και \(\vec{α}\) με \(|\vec{α}|=\dfrac{\sqrt{3}}{2}\), \(|\vec{β}|=\dfrac{1}{2}\) και \(|3\vec{α}+2\vec{β}|=|\vec{α}-2\vec{β}|\).
α) Να αποδείξετε ότι \(\vec{α}\cdot\vec{β}=-\dfrac{3}{8}\).
(Μονάδες 15)
β) Να υπολογίσετε τη γωνία των διανυσμάτων \(\vec{α}\) και \(\vec{β}\).
(Μονάδες 10)
Απάντηση
Έχουμε:
\begin{align}&|\vec{α}|=\frac{\sqrt{3}}{2}\quad &(1)\\ &|\vec{β}|=\frac{1}{2}\quad &(2)\\ &|3\vec{α}+2\vec{β}|=|\vec{α}-2\vec{β}|\quad &(3)\end{align}
α) Από την \((3)\) έχουμε
\begin{align}&|3\vec{α}+2\vec{β}|^2=|\vec{α}-2\vec{β}|^2\\ \iff&(3\vec{α}+2\vec{β})^2=(\vec{α}-2\vec{β})^2\\ \iff&9\vec{α}^2+12\vec{α}\cdot\vec{β}+4\vec{β}^2=\vec{α}^2-4\vec{α}\cdot\vec{β}+4\vec{β}^2\\ \iff&16\vec{α}\cdot\vec{β}=-8\vec{α}^2\\ \iff&\vec{α}\cdot\vec{β}=-\frac{1}{2}\vec{α}^2=-\frac{1}{2}|\vec{α}|^2.\end{align}
Η τελευταία σχέση, λόγω της \((1)\), δίνει
$$\vec{α}\cdot\vec{β}=-\frac{1}{2}\cdot\left(\frac{\sqrt{3}}{2}\right)^2=-\frac{1}{2}\cdot\frac{3}{4}=-\frac{3}{8}.$$
β) Είναι
$$συν(\widehat{\vec{α},\vec{β}})=\frac{\vec{α}\cdot\vec{β}}{|\vec{α}|\cdot|\vec{β}|}.$$
Η τελευταία ισότητα λόγω του ερωτήματος (α) και των \((1)\), \((2)\) δίνει
\begin{align}συν(\widehat{\vec{α},\vec{β}})&=\dfrac{-\dfrac{3}{8}}{\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{2}}\\ &=-\frac{3\cdot 4}{8\cdot\sqrt{3}}\\ &=-\frac{3}{2\cdot\sqrt{3}}\\ &=-\frac{\sqrt{3}}{2},\end{align}
άρα \((\widehat{\vec{α},\vec{β}})=\dfrac{5π}{6}\) ή \(150^o\).
Θέμα: 16427 (ΘΕΜΑ 2ο)
Δίνονται τα σημεία \(A(-2,3)\), \(B(0,8)\), \(Γ(5,3)\) και \(Δ(10,5)\). Να υπολογίσετε:
α) το εσωτερικό γινόμενο \(\overrightarrow{ΑΒ}\cdot\overrightarrow{ΓΔ}\).
(Μονάδες 12)
β) τη γωνία που σχηματίζει το διάνυσμα \(\vec{u}=\overrightarrow{AB}+\overrightarrow{ΓΔ}\) με τον άξονα \(x'x\).
(Μονάδες 13)
Απάντηση
α) Είναι:
\begin{align}\overrightarrow{AB}&=(x_B-x_A,y_B-y_A)\\ &=(0+2,8-3)\\ &=(2,5).\end{align}
Επίσης:
\begin{align}\overrightarrow{ΓΔ}&=(x_Δ-x_Γ,y_Δ-y_Γ)\\ &=(10-5,5-3)\\ &=(5,2).\end{align}
Οπότε:
\begin{align}\overrightarrow{AB}\cdot\overrightarrow{ΓΔ}&=(2,5)\cdot(5,2)\\ &=2\cdot 5+5\cdot 2\\ &=10+10\\ &=20.\end{align}
β) Αν \(ω\) είναι η γωνία που σχηματίζει το διάνυσμα \(\vec{u}\) με τον άξονα \(x'x\), τότε \(λ_\vec{u}=εφω\). Είναι
$$\vec{u}=\overrightarrow{AB}+\overrightarrow{ΓΔ}=(2,5)+(5,2)=(7,7),$$
άρα
$$λ_\vec{u}=\frac{y_\vec{u}}{x_\vec{u}}=\frac{7}{7}=1.$$
Επομένως \(εφω=1\), άρα \(ω=\dfrac{π}{4}\).
Θέμα: 16426 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}=(2,-1)\) και \(\vec{β}=(-3,2)\).
α) Να υπολογίσετε το γινόμενο \(\vec{α}\cdot(2\vec{α}-\vec{β})\).
(Μονάδες 10)
β) Να βρείτε το διάνυσμα \(\vec{γ}=(x,y)\) όταν \(\vec{γ}\perp\vec{α}\) και \(|\vec{γ}|=\sqrt{5}\).
(Μονάδες 15)
Απάντηση
α) Είναι
\begin{align}2\vec{α}-\vec{β}&=2\cdot(2,-1)-(-3,2)\\ &=(4,-2)+(3,-2)\\ &=(7,-4),\end{align}
οπότε
\begin{align}\vec{α}\cdot(2\vec{α}-\vec{β})&=(2,-1)\cdot(7,-4)\\ &=14+4\\ &=18.\end{align}
β) Έχουμε \(\vec{γ}=(x,y)\) και
\begin{align}&\vec{γ}\perp\vec{α}\\ \iff&\vec{γ}\cdot\vec{α}=0\\ \iff&(x,y)\cdot(2,-1)=0\\ \iff&2x-y=0\\ \iff&y=2x.\quad(1)\end{align}
Λόγω της \((1)\), είναι \(\vec{γ}=(x,2x)\). Έτσι,
\begin{align}&|\vec{γ}|=\sqrt{5}\\ \iff&\sqrt{x^2+4x^2}=\sqrt{5}\\ \iff&\sqrt{5x^2}=\sqrt{5}\\ \iff&5x^2=5\\ \iff&x^2=1\\ \iff&x=\pm 1.\end{align}
Για \(x=-1\) είναι \(\vec{γ}=(-1,-2)\), ενώ για \(x=1\) έχουμε \(\vec{γ}=(1,2)\).
Θέμα: 16144 (ΘΕΜΑ 2ο)
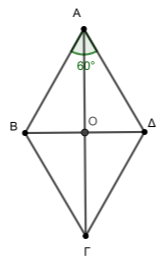
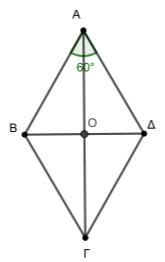
Δίνεται ρόμβος \(ΑΒΓΔ\) με κέντρο \(Ο\), πλευρά \(4\) και \(\hat{Α}=60^ο\). Να υπολογίσετε τα εσωτερικά γινόμενα:
α) \(\overrightarrow{ΑΒ}\cdot\overrightarrow{ΑΔ}\)
β) \(\overrightarrow{ΑΔ}\cdot\overrightarrow{ΒΓ}\)
γ) \(\overrightarrow{ΟΔ}\cdot\overrightarrow{ΑΟ}\)
δ) \(\overrightarrow{ΟΔ}\cdot\overrightarrow{ΟΒ}\)
ε) \(\overrightarrow{ΑΔ}\cdot\overrightarrow{ΓΔ}\)
(Μονάδες 25)
Απάντηση
α)
\begin{align}\overrightarrow{ΑΒ}\cdot\overrightarrow{ΑΔ}&=|\overrightarrow{ΑΒ}|\cdot|\overrightarrow{ΑΔ}|\cdot συν(\widehat{\overrightarrow{ΑΒ},\overrightarrow{ΑΔ}})\\ &=4\cdot 4\cdot συν60^ο\\ &=16\cdot\frac{1}{2}\\ &=8.\end{align}
β) Τα διανύσματα \(\overrightarrow{ΑΔ}\) και \(\overrightarrow{ΒΓ}\) είναι ομόρροπα οπότε σχηματίζουν γωνία \(0^ο\). Οπότε,
\begin{align}\overrightarrow{ΑΔ}\cdot\overrightarrow{ΒΓ}&=|\overrightarrow{ΑΔ}|\cdot|\overrightarrow{ΒΓ}|\cdot συν(\widehat{\overrightarrow{ΑΔ},\overrightarrow{ΒΓ}})\\ &=4\cdot 4\cdot συν0^ο\\ &=16\cdot 1\\ &=16.\end{align}
γ) Οι διαγώνιες του ρόμβου διχοτομούνται, οπότε \(\overrightarrow{ΑΟ}=\overrightarrow{ΟΓ}\), και τέμνονται κάθετα, οπότε τα διανύσματα \(\overrightarrow{ΟΔ}\) και \(\overrightarrow{ΟΓ}\) σχηματίζουν γωνία \(90^ο\) και έχουν εσωτερικό γινόμενο μηδέν. Συνεπώς
$$\overrightarrow{ΟΔ}\cdot\overrightarrow{ΑΟ}=\overrightarrow{ΟΔ}\cdot\overrightarrow{ΟΓ}=0.$$
δ) Το τρίγωνο \(ΑΒΔ\) είναι ισοσκελές αφού οι δυο πλευρές του είναι πλευρές του ρόμβου, με γωνία της κορυφής \(60^ο\). Άρα το τρίγωνο \(ΑΒΔ\) είναι ισόπλευρο με πλευρά \(4\). Το \(Ο\) είναι το σημείο τομής των διαγωνίων του ρόμβου, οπότε \(ΒΟ=ΟΔ=2\). Άρα είναι
\begin{align}\overrightarrow{ΟΔ}\cdot\overrightarrow{ΟΒ}&=|\overrightarrow{ΟΔ}|\cdot|\overrightarrow{ΟΒ}|\cdot συν(\widehat{\overrightarrow{ΟΔ},\overrightarrow{ΟΒ}})\\ &=2\cdot 2\cdot συν180^ο\\ &=4\cdot (-1)\\ &=-4.\end{align}
ε) Για τη γωνία \((\widehat{\overrightarrow{ΑΔ},\overrightarrow{ΓΔ}})\) ισχύει
$$(\widehat{\overrightarrow{ΑΔ},\overrightarrow{ΓΔ}})=(\widehat{\overrightarrow{ΑΔ},\overrightarrow{ΒΑ}})=180^ο-60^ο=120^ο.$$
Οπότε,
\begin{align}\overrightarrow{ΑΔ}\cdot\overrightarrow{ΓΔ}&=|\overrightarrow{ΑΔ}|\cdot|\overrightarrow{ΓΔ}|\cdot συν(\widehat{\overrightarrow{ΑΔ},\overrightarrow{ΓΔ}})\\ &=4\cdot 4\cdot συν120^ο\\ &=16\cdot \left(-\frac{1}{2}\right)\\ &=-8.\end{align}
Θέμα: 16141 (ΘΕΜΑ 2ο)
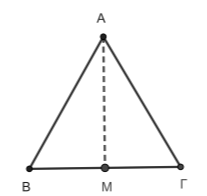
Δίνεται ισόπλευρο τρίγωνο \(ΑΒΓ\) πλευράς \(10\) και το μέσο \(Μ\) της πλευράς \(ΒΓ\).
α) Να βρεθούν τα μέτρα των γωνιών:
i. \((\widehat{\overrightarrow{ΑΒ},\overrightarrow{ΑΓ}})\).
ii. \((\widehat{\overrightarrow{ΑΜ},\overrightarrow{ΒΓ}})\).
iii. \((\widehat{\overrightarrow{ΑΜ},\overrightarrow{ΓΑ}})\).
iv. \((\widehat{\overrightarrow{ΒΜ},\overrightarrow{ΓΜ}})\).
v. \((\widehat{\overrightarrow{ΓΜ},\overrightarrow{ΓΒ}})\).
β) Να υπολογιστούν τα εσωτερικά γινόμενα:
i. \(\overrightarrow{ΑΜ}\cdot\overrightarrow{ΒΓ}\).
ii. \(\overrightarrow{ΑΜ}\cdot\overrightarrow{ΓΑ}\).
iii. \(\overrightarrow{ΓΜ}\cdot\overrightarrow{ΓΒ}\).
Απάντηση
α)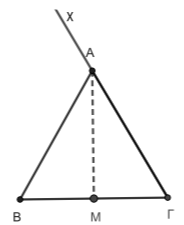
i. \((\widehat{\overrightarrow{ΑΒ},\overrightarrow{ΑΓ}})=60^\circ\).
ii. \((\widehat{\overrightarrow{ΑΜ},\overrightarrow{ΒΓ}})=90^\circ\).
iii. \((\widehat{\overrightarrow{ΑΜ},\overrightarrow{ΓΑ}})=\widehat{xΑΜ}=180^\circ-30^\circ=150^\circ\), καθώς η διάμεσος προς τη βάση είναι και διχοτόμος της γωνίας της κορυφής.
iv. \((\widehat{\overrightarrow{ΒΜ},\overrightarrow{ΓΜ}})=180^\circ\).
v. \((\widehat{\overrightarrow{ΓΜ},\overrightarrow{ΓΒ}})=0^\circ\).
β) Τα μέτρα των διανυσμάτων \(\overrightarrow{ΑΒ}, \overrightarrow{ΑΓ}\) και \(\overrightarrow{ΒΓ}\) είναι \(10\) αφού το τρίγωνο είναι ισόπλευρο. Για το μέτρο του διανύσματος \(\overrightarrow{ΑΜ}\) έχουμε από το πυθαγόρειο θεώρημα στο τρίγωνο \(ΑΜΓ\):
\begin{align}&ΑΜ^2=ΑΓ^2-ΜΓ^2\\ \iff&ΑΜ^2=10^2-5^2=75\\ \iff&ΑΜ^2=25\cdot 3\\ \iff&ΑΜ=5\sqrt{3}.\end{align}
i.
\begin{align}\overrightarrow{ΑΜ}\cdot\overrightarrow{ΒΓ}&=|\overrightarrow{ΑΜ}||\overrightarrow{ΒΓ}|συν(\widehat{\overrightarrow{ΑΜ},\overrightarrow{ΒΓ}})\\ &=5\sqrt{3}\cdot 10\cdot συν90^\circ\\ &=0.\end{align}
ii.
\begin{align}\overrightarrow{ΑΜ}\cdot\overrightarrow{ΓΑ}&=|\overrightarrow{ΑΜ}||\overrightarrow{ΓΑ}|συν(\widehat{\overrightarrow{ΑΜ},\overrightarrow{ΓΑ}})\\ &=5\sqrt{3}\cdot 10\cdot συν150^\circ\\ &=50\sqrt{3}\cdot(-\frac{\sqrt{3}}{2})\\ &=75.\end{align}
iii.
\begin{align}\overrightarrow{ΓΜ}\cdot\overrightarrow{ΓΒ}&=|\overrightarrow{ΓΜ}||\overrightarrow{ΓΒ}|συν(\widehat{\overrightarrow{ΓΜ},\overrightarrow{ΓΒ}})\\ &=5\sqrt{3}\cdot 10\cdot συν0^\circ\\ &=5\cdot 10\cdot 1\\ &=50.\end{align}
Θέμα: 15996 (ΘΕΜΑ 2ο)
Δίνονται τα σημεία \(A(-6,-1)\), \(B(8,7)\), \(Γ(-10,6)\), τα οποία ορίζουν τρίγωνο \(ABΓ\).
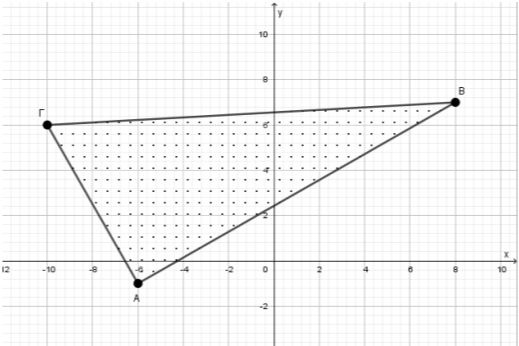
α) Να βρείτε τις συντεταγμένες των διανυσμάτων \(\overrightarrow{AB}\), \(\overrightarrow{ΒΓ}\) και του αθροίσματος τους \(\overrightarrow{AB}+\overrightarrow{ΒΓ}\).
(Μονάδες 10)
β) Ένας μαθητής βλέποντας το τρίγωνο \(ABΓ\) ισχυρίστηκε ότι είναι ορθογώνιο. Να ελέγξετε την αλήθεια του ισχυρισμού.
(Μονάδες 15)
Απάντηση
α) Είναι
\begin{align}&\overrightarrow{AB}=(8-(-6),7-(-1))=(14,8),\\ &\overrightarrow{ΒΓ}=(-10-8,6-7)=(-18,-1)\end{align}
και
$$\overrightarrow{AB}+\overrightarrow{BΓ}=(14+(-18),8+(-1))=(-4,7).$$
β)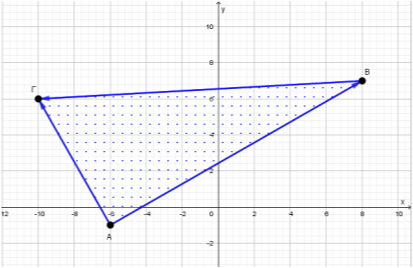
Στο σχήμα “φαίνεται” ότι το τρίγωνο \(ABΓ\) είναι ορθογώνιο, με ορθή γωνία την \(\hat{A}\). Αλλά είναι αναγκαία η μαθηματική απόδειξη του ισχυρισμού. Πραγματικά είναι
\begin{align}\overrightarrow{AB}\cdot\overrightarrow{ΑΓ}&=14\cdot (-4)+8\cdot7\\ &=-56+56\\ &=0.\end{align}
Επομένως, τα διανύσματα \(\overrightarrow{AΒ}\) και \(\overrightarrow{AΓ}\) είναι κάθετα.
Εναλλακτική προσέγγιση:
Έχουμε \(λ_{ΑΒ}=\dfrac{4}{7}\), \(λ_{AΓ}=-\dfrac{7}{4}\) και άρα \(λ_{ΑΒ}\cdot λ_{ΑΓ}=-1\).
Θέμα: 15825 (ΘΕΜΑ 2ο)
Θεωρούμε τα διανύσματα \(\vec{α},\vec{β}\) με \(|\vec{α}|=2,|\vec{β}|=4,(\widehat{\vec{α},\vec{β}})=\dfrac{π}{3}\) και το \(\vec{γ}=\vec{α}-\vec{β}\).
α) Να αποδείξετε ότι \(\vec{α}\cdot\vec{β}=4\).
(Μονάδες 8)
β) Να αποδείξετε ότι \(\vec{α}\cdot\vec{γ}=0\).
(Μονάδες 10)
γ) Να βρείτε τη \((\widehat{\vec{α},\vec{γ}})\).
(Μονάδες 7)
Απάντηση
α) Είναι
\begin{align}\vec{α}\cdot\vec{β}&=|\vec{α}|\cdot|\vec{β}|\cdot συν(\widehat{\vec{α},\vec{β}})\\ &=2\cdot 4\cdot συν\frac{π}{3}\\ &=8\cdot\frac{1}{2}\\ &=4.\end{align}
β) Είναι
\begin{align}\vec{α}\cdot\vec{γ}&=\vec{α}\cdot(\vec{α}-\vec{β})\\ &=\vec{α}^2-\vec{α}\cdot\vec{β}\\ &=|\vec{α}|^2-4\\ &=4-4\\ &=0.\end{align}
γ) Είναι
$$\vec{α}\cdot\vec{γ}=0\iff\vec{α}\perp\vec{γ}\iff(\widehat{\vec{α},\vec{γ}})=\frac{π}{2}.$$
Θέμα: 15463 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\overrightarrow{ΑΒ}=(2,1)\) και \(\overrightarrow{ΑΓ}=(3,-1).\)
α) Να αποδείξετε ότι \(\overrightarrow{ΒΓ}=(1,-2).\)
(Μονάδες 8)
β) Να αποδείξετε ότι \(\overrightarrow{ΑΒ} \perp \overrightarrow{ΒΓ}.\)
(Μονάδες 9)
γ) Να αποδείξετε ότι: \(|\overrightarrow{ΑΒ}| = |\overrightarrow{ΒΓ}|.\)
(Μονάδες 8)
Απάντηση
α) Είναι
$$\begin{align} \overrightarrow{ΒΓ} & = \overrightarrow{AΓ} - \overrightarrow{AB} \\ & = (3,-1) - (2,1) \\ & = (1,-2). \end{align}$$
β) Είναι:
$$\overrightarrow{ΑΒ} \cdot \overrightarrow{ΒΓ} = (2,1)\cdot (1,2)=2-2=0$$
γ) Είναι
$$|\overrightarrow{ΑΒ}|=\sqrt{2^2+1^2}=\sqrt{5}$$
και
$$|\overrightarrow{ΒΓ}|=\sqrt{1^2+(-2)^2}=\sqrt{5}$$
Oπότε: \(|\overrightarrow{ΑΒ}| = |\overrightarrow{ΒΓ}|.\)
Θέμα: 15379 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}=(1,3),\ \vec{β} =(3,−1)\).
Να υπολογίσετε:
α) το εσωτερικό γινόμενο \(\vec{α} \cdot \vec{β}\) και τη γωνία μεταξύ των δύο διανυσμάτων \(\vec{α},\ \vec{β}.\)
(Μονάδες 13)
β) το διάνυσμα \(\vec{γ} =2\vec{α} - \vec{β}\)
(Μονάδες 12)
Απάντηση
α) Το εσωτερικό γινόμενο των διανυσμάτων \(\vec{α},\ \vec{β}\) δίνεται από τον τύπο
\begin{align} \vec{α} \cdot \vec{β} & = x_1 \cdot x_2 + y_1 \cdot y_2 \\ & =1\cdot 3+3\cdot (−1) \\ & =3−3 \\ & =0\end{align}
Επειδή \(\vec{α} \cdot \vec{β}=0\) αν και μόνο αν \(\vec{α} \perp \vec{β}\), δηλαδή τα διανύσματα είναι μεταξύ τους κάθετα και η γωνία μεταξύ των διανυσμάτων \(\vec{α},\ \vec{β}\) είναι ορθή.
β) Δίνονται οι συντεταγμένες των διανυσμάτων \(\vec{α},\ \vec{β}\), τότε:
\begin{align} \vec{γ} & =2\vec{α} - \vec{β} \\ & =2\cdot (1,3) - (3,-1) \\ & =(2,6)-(3,-1) \\ & =(-1,7)\end{align}
Θέμα: 15317 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{v}=(3,0)\) και \(\vec{w}=(-3,4)\).
α) Να δείξετε ότι τα διανύσματα δεν είναι παράλληλα.
(Μονάδες 12)
β) i. Στο παρακάτω σύστημα συντεταγμένων να σχεδιάσετε τα διανύσματα \(\vec{v}\) και \(\vec{w}.\)
(Μονάδες 10)
- Να προσδιορίσετε το είδος της γωνίας \(θ\) που σχηματίζουν τα διανύσματα.
(Μονάδες 3)
Απάντηση
α) Τα διανύσματα δεν είναι παράλληλα, διότι:
$$det(\vec{v},\vec{w})=\begin{vmatrix} 3 & 0 \\ -3 & 4 \end{vmatrix}=12-0=12\neq0$$
β) i. Στο σύστημα συντεταγμένων σχεδιάζουμε τα διανύσματα \(\vec{v}=(3,0)\) και \(\vec{w}=(-3,4)\) ως εξής: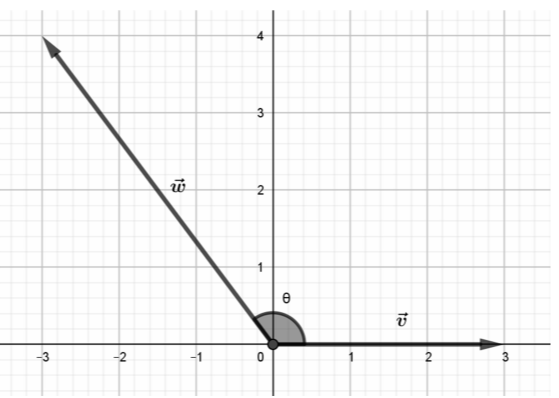
- Με βάση το σχήμα στο βi) ερώτημα, η γωνία \(θ\) που σχηματίζουν τα διανύσματα είναι αμβλεία.
Θέμα: 15186 (ΘΕΜΑ 2ο)
Δίνονται τα σημεία \(Α(2,1)\), \(Β(6,3)\), \(Δ(1,-2)\) και \(Γ(9,2)\). Να αποδείξετε ότι:
α) Το μέσο \(Μ\) του τμήματος \(ΑΒ\) έχει συντεταγμένες \((4,2)\) και το μέσο \(Ν\) του τμήματος \(ΓΔ\) έχει συντεταγμένες \((5,0)\).
(Μονάδες 8)
β) \(\overrightarrow{MN}=(1,-2)\) και \(\overrightarrow{ΔΓ}=(8,4)\).
(Μονάδες 8)
γ) \(\overrightarrow{MN}\perp\overrightarrow{ΔΓ}\).
(Μονάδες 9)
Απάντηση
α) Αν \(Μ(x_M,y_M)\) και \(Ν(x_N,y_N)\), είναι
\begin{align}&x_M=\frac{6+2}{2}=4,\\ &y_M=\frac{3+1}{2}=2\end{align}
και
\begin{align}&x_N=\frac{9+1}{2}=5,\\ &y_N=\frac{2-2}{2}=0.\end{align}
β) Είναι
$$\overrightarrow{MN}=(5-4,0-2)=(1,-2)$$
και
$$\overrightarrow{ΔΓ}=(9-1,2-(-2))=(8,4).$$
γ) 'Εχουμε ότι
\begin{align}\overrightarrow{MN}\cdot\overrightarrow{ΔΓ}&=(1,-2)\cdot(8,4)\\ &=1\cdot8+(-2)\cdot4\\ &=8-8\\ &=0.\end{align}
Άρα \(\overrightarrow{MN}\perp\overrightarrow{ΔΓ}\).
Θέμα: 15073 (ΘΕΜΑ 2ο)
Δίνονται τα διανύσματα \(\vec{α}=(1,2)\) και \(\vec{β}=(2,3)\).
α) Να βρείτε τις συντεταγμένες του διανύσματος \(\vec{γ}=2\vec{α}+\vec{β}\).
(Μονάδες 8)
β) Να βρείτε το μέτρο του διανύσματος \(\vec{γ}\).
(Μονάδες 8)
γ) Να βρείτε το εσωτερικό γινόμενο \(\vec{α} \cdot \vec{γ}\).
(Μονάδες 9)
Απάντηση
α) Είναι: \(\vec{γ}=2\vec{α}+\vec{β}=2 \cdot (1,2) + (2,3)=(2+2,4+3)=(4,7)\).
β) Έχουμε: \(|\vec{γ}|=\sqrt{4^2+7^2}=\sqrt{16+49}=\sqrt{65}\).
γ) Βρίσκουμε το εσωτερικό γινόμενο \(\vec{α} \cdot \vec{γ}=(1,2) \cdot (4,7)= 1 \cdot 4 + 2 \cdot 7 = 18\).
Θέμα: 15038 (ΘΕΜΑ 2ο)
Θεωρούμε διανύσματα \(\vec{α},\ \vec{β}\) τέτοια ώστε \(|\vec{α}|=3,\ |\vec{β}|=4\) και \((\widehat{\vec{α},\vec{β}})=\dfrac{π}{3}\).
α) Να βρείτε το εσωτερικό γινόμενο των διανυσμάτων \(\vec{α},\ \vec{β}\).
(Μονάδες 9)
β) Να βρείτε τα \(\vec{α}^2\) και \(\vec{β}^2\).
(Μονάδες 6)
γ) Να αποδείξετε ότι
$$(3\vec{α}-\vec{β})\cdot (\vec{α}-3\vec{β})=15.$$
(Μονάδες 10)
Απάντηση
α) Το εσωτερικό γινόμενο των διανυσμάτων \(\vec{α},\ \vec{β}\) δίνεται από το τύπο
\begin{align}\vec{α}\cdot\vec{β}&=|\vec{α}||\vec{β}|συν(\widehat{\vec{α},\vec{β}})\\ &=3\cdot 4\cdot συν\frac{π}{3}\\ &=12\cdot\frac{1}{2}\\ &=6.\end{align}
Άρα \(\vec{α}\cdot\vec{β}=6\).
β)
$$\vec{α}^2=|\vec{α}|^2=3^2=9$$
και
$$\vec{β}^2=|\vec{β}|^2=4^2=16.$$
γ)
\begin{align}&\phantom{{}={}}(3\vec{α}-\vec{β})\cdot(\vec{α}-3\vec{β})\\ &=3\vec{α}^2-\vec{β}\cdot\vec{α}-9\vec{α}\cdot\vec{β}+3\vec{β}^2\\ &=3\vec{α}^2-10\vec{α}\cdot\vec{β}+3\vec{β}^2\\ &=3\cdot 9-10\cdot 6+3\cdot 16\\ &=15.\end{align}
